Висловлення. Операції над висловленнями

Математична логіка - це наука, яка займається вивченням закономірностей логічних обґрунтувань в математиці. Основним об'єктом математичної логіки є висловлення.

Висловлення– це речення, про яке можна сказати істинне воно чи хибне.

Позначатимемо висловлення великими літерами латинського алфавіту: A, B, C, X₁, X₂, …

Наприклад: "Кіт Гаврюша щодня їсть сметану",

"Чим далі в ліс, тим своя сорочка ближче до тіла".

Не висловлення: "Іван Іванович"

"Хай йому грець!"

"Ці мідії – дуже смачні" (дехто їх взагалі терпіти не може).

Якщо висловлення А – істинне, то це позначається так: p(А) = 1, якщо В - хибне, то p(А) = 0 (ми таким позначенням не будемо користуватись).

Висловлення бувають прості і складні. Складні утворюються з простих за допомогою логічних операцій. Що таке операція Ви дізнаєтесь пізніше, а поки що розпочнемо серію означень логічних операцій.

Запереченням висловлення Аназивається висловлення "не А" (позначається 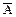), яке істинне тоді і тільки тоді, коли А – хибне. Краще означити заперечення за допомогою таблиці:

А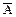

Наприклад: "Не вірно, що кіт Гаврюша щодня їсть сметану".

Кон'юнкцією висловлень А і Вназивається висловлення "А і В" (позначається АВ, для позначення кон’юнкції часто вживаються символи Ù та &), яке істинне тоді і тільки тоді, коли А і В істинні.

А	В	АВ

Наприклад: " На городі – бузина, а в Києві – дядько", тут

А: "На городі росте бузина" (мається на увазі конкретний город),

В: "В Києві живе дядько" (мається на увазі конкретний племінник).

Вправа. Запишіть словами означення інших логічних операцій, заданих таблицями істинності.

Диз'юнкція– "А або В", позначається (АÚВ)

А	В	АÚВ

Наприклад: "2×2 ³ 5", тут:

А: "2×2 > 5",

В: "2×2 = 5".

Імплікація– "якщо А, то В", позначається (А Þ В)

А	В	АÞВ

Наприклад: "Якщо стукнути кобилу по носі – махне хвостом", тут:

А: "Стукнути кобилу по носі",

В: "Кобила махне хвостом".

Еквіваленція– "А тоді і тільки тоді, коли В", позначається (А Û В)

А	В	АÛВ

Наприклад: "Для того, щоб Ви вірно засвоїли означення еквіваленції, необхідно і достатньо, щоб Ви змогли самостійно навести правильний приклад еквіваленції" (слова "тоді і тільки тоді" з успіхом можна замінити словами "необхідно і достатньо").

Під логічною формулою[1]будемо розуміти будь-яке просте висловлення, а також складне висловлення, складене із простих висловлень та логічних формул за допомогою логічних операцій.

Наприклад: 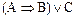– логічна формула, 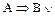– не формула.

Логічні формули теж позначають великими літерами латинського алфавіту.

Порядок виконання основних логічних операцій такий: заперечення, кон’юнкція, диз’юнкція, імплікація (еквіваленція).

Завдання.Спробуйте запропоновані висловлення розбити на прості висловлення, позначити прості висловлення латинськими літерами та записати у спрощеному вигляді за допомогою основних логічних операцій:

1) ”Якщо дядько Степан їв сьогодні борщ і сало з часником, то він не піде на зустріч з англійською королевою”;

2) “Кіт Гаврюша тоді і тільки тоді йде ловити мишей, коли він не спить і нічого не їв не менше трьох днів”.

Задача.Запишіть скорочено діалог Бобчинського з Добчинським та виясніть, хто сказав: “Е!”, якщо відомо, що із 10 висловів, істинними є лише непарна кількість:

Б.: “Це Ви, Петре Івановичу, першим сказали: “Е!”. Ви самі раніше так говорили”.

Д.: “Ні, Петре Івановичу, я так не говорив. Це Ви сьомгу першим замовили, Ви і сказали: “Е!” . А в мене зуб у роті свистить”.

Б.: “Що я сьомгу першим замовляв, це правда. Вірно і те, що у Вас зуб свистить. Але все-таки це Ви першим сказали: “Е!”

Для логічних формул можна будувати таблиці істинності. Розглянемо приклад. Складемо таблицю істинності для логічної формули .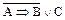

А	В	С	А Þ В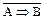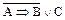

Задача. У таблиці істинності, яку ми склали для формули від трьох простих висловлень 8 рядків. Скільки рядків у таблиці істинності для формули від двох простих висловлень? від n висловлень?

Завдання. Складіть таблиці істинності для формул:

1) ;

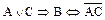2) А Þ ВС Þ В;

3) ;

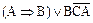4) .

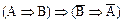Дві логічні формули називаються рівносильними, якщо вони приймають однакові значення істинності при підстановці значень істинності простих висловлень, іншими словами, якщо їх таблиці істинності співпадають. Рівносильність формул позначається так: А º В.

Задача.Скільки існує різних нерівносильних формул від двох простих висловлень? від n?

Логічні формули, які при довільних значеннях істинності простих висловлень приймають значення істинності рівне 0, називаються тотожно хибними.

Завдання. Наведіть приклад тотожно хибної формули.

Логічні формули, які при довільних значеннях істинності простих висловлень приймають значення істинності рівне 1, називаються тотожно істинними формулами, тавтологіями або логічними законами.

Деякі з логічних законів мають свої назви, наприклад:

1) 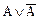– закон виключення третього;

2) 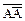– закон протиріччя;

3) 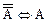– закон подвійного заперечення;

4) 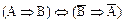– закон контрапозиції;

5) А(А Þ В) Þ В – modus ponens (стверджувальний модус);

6) 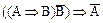– modus tollens (заперечувальний модус);

7) (А Þ В)(В Þ С) Þ (А Þ С) – закон силогізму.

Завдання. Перевірте на вибір справедливість трьох логічних законів за допомогою таблиць істинності.

Задача. Ми навели означення п'яти основних логічних операцій (заперечення, кон’юнкції, диз’юнкції, імплікації та еквіваленції; ці операції часто називають булевими). А скільки всього можна придумати різних операцій від двох змінних?

Якщо Вам не вдалося розв'язати запропоновану задачу, то придивіться до такої таблиці:

A

B

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C14

C15

C16

В цій таблиці: C₁ º 0 – тотожно хибна формула (інколи замість 0 пишуть F від англ. "false" – хиба),

C₂ º AB,

C₃ º 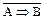- ліва коімплікація,

C₄ º A,

C₅ º 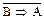- права коімплікація,

C₆ º B,

C₇ º AÅ B – альтернативна диз'юнкція,

C₈ º AÚ B,

C₉ º 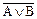- функція Вебба,

C₁₀ º AÛB,

C₁₁ º ,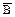

C₁₂ º BÞA – права імплікація,

C₁₃ º ,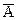

C₁₄ º AÞB,

C₁₅ º 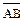º A½B – штрих Шеффера,

C₁₆ º 1 – тотожно істинна формули (інколи замість 1 пишуть Т від англ. "true" – істина),

Задача. Скільки існує булевих операцій від трьох змінних? від n змінних?

Завдання.Виразіть основні логічні операції через:

1) кон’юнкцію і заперечення;

2) імплікацію і заперечення;

3) еквіваленцію і заперечення;

4) альтернативну диз’юнкцію і кон’юнкцію (так зване представлення у вигляді полінома Жегалкіна);

5) через якусь одну логічну операцію.

Задача. Перевірте правильність висловлення:

Якщо Джонс не зустрічав цієї ночі Сміта, то або Сміт - убивця, або Джонс каже неправду. Якщо Сміт – не вбивця, то Джонс не зустрічав Сміта цієї ночі, і вбивство сталося опівночі. Якби вбивство сталося опівночі, то або Сміт убивця, або Джонс каже неправду. Значить, Сміт – убивця.