Схемы дедуктивных умозаключений
Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения?
В логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения.
1. Правило заключения ( А(х) ÞВ(х), А(а) ) Þ В(а).
А(х)ÞВ(х) – общая посылка,
А(а) – частная посылка,
В(а) – заключение.
Пример использования правила заключения. Если запись числа оканчивается цифрой 5, то число делится на 5. Запись числа 135 заканчивается цифрой 5. Значит число 135 делится на 5.
2. Правило отрицания ( А(х) ÞВ(х), 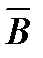 (а) ) Þ
(а) ) Þ 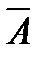 (а).
(а).
А(х)ÞВ(х) – общая посылка,
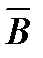 (а) – частная посылка,
(а) – частная посылка,
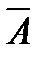 (а) – заключение.
(а) – заключение.
Пример использования правила отрицания. Если запись числа оканчивается цифрой 5, то число делится на 5. Число 177 не делится на 5. Значит его запись не оканчивается цифрой 5.
3.Правило силлогизма (А(х) ÞВ(х), В(х) ÞС(х)) Þ (А(х) ÞС(х))
А(х)ÞВ(х) и В(х)Þ С(х) - посылки
А(х)ÞС(х) – заключение.
Пример использования правила силлогизма. Если число кратно 12, то оно кратно 6. Если число кратно 6, то оно кратно 3. Значит , если число кратно 12, то оно кратно 3.
