Определение вероятности события

Пусть из 100 студентов, среди которых 97 не знают иностранного языка, а остальные знают, выбирается один человек. Очевидно, что события А и В, состоящие соответственно в том, что студент знает и не знает язык, не равновозможные; событие В более возможно, более вероятно, чем А.

Под вероятностью события понимается число, являющееся характеристикой степени объективной возможности наступления этого события. Вероятность события А обозначают символом Р(А) (от лат. рrobabilitas – «вероятность»).

Если множество 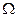состоит из n равновозможных элементарных событий, то Р(А) события А равна числу m элементарных событий, входящих в А ( благоприятствующих А), деленному на число всех элементарных событий, т.е.

Р(А)= .

Это определение вероятности называется классическим.

Пример:из условий примера в начале параграфа определить вероятность того, что выбранный наудачу студент знает иностранный язык.

Этому событию благоприятствуют три элементарных события из 100 возможных. Следовательно, Р(А)= =0,03.

Теорема 1.Вероятность любого события есть неотрицательное число, не превосходящее единицы.

Число m случаев, благоприятствующих любому событию, не может быть отрицательным и большим, чем их общее число n, т.е. 0 . Разделив это неравенство на n, получим , или .

Теорема 2.Вероятность достоверного события равна единице.

Это очевидно, т.к. достоверному событию благоприятствуют n элементарных событий из n возможных.

Теорема 3. Вероятность невозможного события равна 0.

Необходимо четко различать понятия вероятности и частости события. Вероятность события вычисляется до опытов и численно выражает меру объективной возможности наступления события, а частость его определяется лишь после того, как результаты опыта становятся известными.

Пример: монета подброшена 5 раз, «орел» выпал 2 раза. Каковы вероятность и частость выпадения «орла»?

Вероятность выпадения «орла» =0,4 (из двух возможных исходов «орлу» благоприятствует 1). Частость -- =0,4(событие наступило два раза в пяти испытаниях).

Чем больше число испытаний проводится, тем ближе значения частости и вероятности события.

Задачи.

1. Брошены три монеты. Найти вероятность того, что выпадут два «орла».
2. Бросают игральную кость. Какова вероятность выпадания номера 4 на верхней грани упавшей на стол кости? Какова вероятность выпадания номера, большего 4?
3. При стрельбе была получена частость попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов?
4. Брошены две игральные кости. Какова вероятность выпадания на двух костях в сумме не менее 9 очков? Какова вероятность выпадания единицы, по крайней мере, на одной кости?
5. Из пяти карточек с буквами А,Б,В,Г,Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово «ДВА»?
6. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся черными?
7. Ребенок играет с четырьмя буквами разрезной азбуки А,А,М,М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»?
8. А и В и еще 8 человек стоят в очереди. Определить вероятность того, что А и В отделены друг от друга тремя лицами.
9. Среди 17 студентов группы, из которых восемь девушек, разыгрывается семь билетов, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся четыре девушки?