Расчет кнд интерференционных систем

Выражение /13/ в общем случае можно считать достаточным для расчета значений КНД во всем исследуемом диапазоне Dt/T. Однако нам правило неизвестно аналитическое выражение формы сигнала. В этом случае для ориентировочной оценки свойств интерференционных систем целесообразно заменить функцию ƒ(t) каким - либо другим выражением, удовлетворительно аппроксимирующим ее. В работе /I/ для этой цели использован импульс Пузырева:

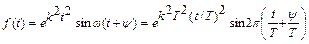, (18)

где К – коэффициент затухания огибающей экспоненты;

ω – круговая частота гармонической заполняющей;

ψ – фазовый сдвиг.

Форма импульса для различных значении К и ψ представлена на рис.З. Легко видеть, что изменяя величину γ=к²Т² и сдвиг ψ можно управлять формой сигнала и варьировать ею в широких пределах.

Достоинствами импульса Пузырева являются:

- близость формы импульса к форма сейсмических сигналов;

- сосредоточенность основной энергии импульса в ограниченном интервале времени, т.е. он достаточно быстро затухает;

- ограниченность его спектра вследствие того, что сам импульс не ограничен во времени;

- простота подбора параметров.

- 12 -

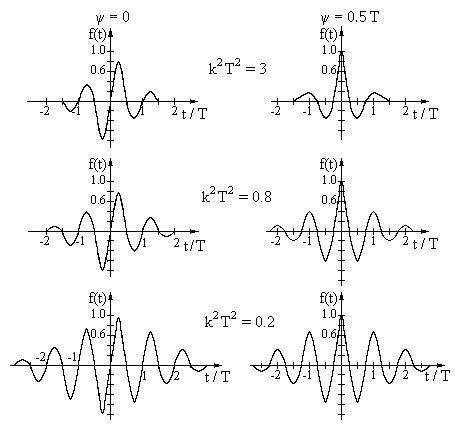
Рис 3 формы импульса Пузырева.

Подставив выражение /18/ в формулу /14/ получим явное выражение КНД и можно показать, что интегралы, полученные в результате подстановки будут иметь следующие значения:

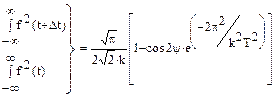
- 13 -

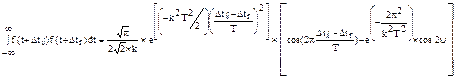
Величина 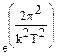в реальном интервале 0.2 ≤ к²Т²≥3 пренебрежительно мала (не превышает 0.001), следовательно мало и произведение ее на cos 2 ψ, поэтому вторыми слагаемыми в скобках можно пренебречь. Отсюда:

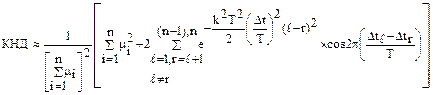(19)

Для частного случая однородной системы:

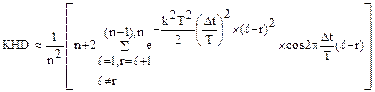(20)

Как видно из (19) и (20) расчет значений КНД а достаточно широком диапазоне значений аргумента Dt/T может быть выполнен только с помощью ЭВМ. В этом случае для описания параметров интерференционных систем используется понятие амплитудно-временного аналога (ABA). АВА содержит распределение чувствительности и запаздываний некоторой идеально-регулярной волны на входах системы. На основании ABA может быть рассчитана одна и только одна точка на графике КНД исследуемой интерференционной системы. Для расчета всего графика требуется составление серии аналогов. Как правило, эта работа не является трудоемкой, поскольку на волновое поле в конкретных расчетах накладываются определенные ограничения (например – распространение плоских волн) и вычисление временных запаздываний происходит в процессе расчета КНД на ЭВМ. Легко видеть, что АВА не зависит от физической сущности интерференционной системы, а зависит только от параметров системы и вол­нового поля, т.е. отражает структуру интерференции. Однако ABA рассматривает лишь те характеристики интерференции, которые наиболее существенны в рамках энергетической теории, опуская при этом, к примеру, спектральный состав колебаний (последний описывается лишь формой импульса и преобладающим периодом). В этом смысле говорят, что амплитудно-временной аналог отражает главную структуру интерференции .

- 14 -

Форма записи ABA: μ_i : μ₁ μ₂ μ₃ μ₄ μ₅

* * * * *

Δt_i: Δt₁ Δt₂ Δt₃ Δt₄ Δt₅

Здесь * – условное обозначение элемента системы, где μ_i ≠ 0, а запаздывание
i -той волны – Δt_i.

Таким образом, по заданным параметрам импульса (к, Т, ψ) и серии амплитудно- временных аналогов можно рассчитать график КНД, описывающий свойства конкретной интерференционной системы. Естественно, что разным параметрам импульса будут соответствовать и разные графики КНД. Обычно рассматриваются двухпериодные (γ = к²Т² =3), трехпериодные (γ = 0.8) и реже – пятипериодные импульсы (γ=0.2).