Обозначение классов точности средств измерений

Согласно ГОСТ 8.401-80, для указания нормированных значений погрешности чувствительности γ_s, приведённой аддитивной погрешности γ₀, приведённых погрешностей в начале γ_н и конце γ_к диапазона измерений не могут использоваться произвольные числа. Выраженные в процентах, они могут иметь значения 6 – 4 – 2,5 – 1,5 – 1,0 – 0,5 – 0,2 – 0,1 – 0,05 – 0,02 – 0,01 – 0,005 – 0,002 – 0,001 и т. д.

Значение класса точности прибора маркируется на его шкале. Для того чтобы различить, какая из погрешностей обозначена в точности, используются следующие условные обозначения.

Если класс точности прибора установлен по значению погрешности чувствительности γ_s, т.е. форма полосы погрешности условно принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком. Например, 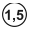обозначает, что γ_s = 1,5%.

Если же полоса погрешностей принята аддитивной и прибор в качестве класса нормируется приведённой погрешностью нуля γ₀ (таких приборов большинство), то класс точности указывается без каких-либо подчеркиваний (например, просто 1,5).

Наконец, на приборах с резко неравномерной шкалой, например омметрах, класс точности прибора указывается в долях от длины шкалы и обозначается .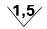

Обозначение класса точности в виде, например, 0,02/0,01 указывает, что погрешность прибора нормирована по двучленной формуле с γ_н = 0,01% и γ_к = 0,02%.

Обозначение класса прибора дает достаточно полную информацию для вычисления приближённой оценки погрешностей результатов измерения.

Некоторые практические замечания

Хотя ГОСТ 8.401-80 направлен на то, чтобы нормирование погрешностей СИ производилось единообразно, в измерительной практике такого единообразия пока ещё нет, так как используется большое число хороших высокоточных приборов, которые были выпущены ещё до введения этого стандарта, закупаются и широко используются приборы иностранного производства, нормированные, естественно, не в соответствии с ГОСТ 8.401-80, и т. д.

Например, погрешность высокоточных потенциометров постоянного тока нормируется чаще всего двучленной формулой (*), а класс точности прибора указывается в виде одного числа – его относительной погрешности чувствительности. В этом случае указание класса точности в виде одного числа γ_s не является признаком того, что прибор не имеет аддитивной составляющей погрешности, и потребитель обязан быть внимательным при расчёте погрешностей результатов измерения, чтобы не допустить ошибки.

При нормировании погрешностей сложных СИ двучленной формулой (**) ГОСТ 8.401-80 предусматривает несколько иное ее написание, когда текущее значение относительной погрешности γ(х) выражается не через значение аддитивной γ_н и мультипликативной γ_s составляющих предела допускаемых погрешностей, как в формуле (**), а через указываемые в обозначении класса точности приведенные погрешности в начале γ_н и в конце γ_к диапазона измерений. В этом случае, учитывая, что

γ_к = γ_н + γ_s,

соотношение (**) принимает вид

. (****)

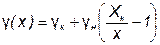На практике это соотношением более удобно использовать для вычисления γ(x) по известным х, X_к, γ_н и γ_к.

У весьма широкодиапазонных приборов, например, мостов для измерения сопротивлений, в их технической документации вместо указания коэффициентов трёхчленной формулы (***) часто приводятся просто диапазоны, в которых погрешность результата измерения не превосходит указанного значения.

Например, указывается, что относительная погрешность не превосходит:

0,5% в диапазоне от 102 до 104 Ом;

1% – от 5 до 105 Ом;

5% – от 0,5 до 106 Ом;

10% – от 0,2 до 2·106 Ом;

20% – от 0,1 до 4·106 Ом.

Эти данные достаточно точно соответствуют трёхчленной формуле (***).

Поэтому по ним можно определить коэффициенты Δ_o, Δ_∞ и γ_s формулы (***) и использовать её для аналитического определения γ(х) при любом произвольном значении х.

Так, например, приведённым выше данным соответствует Δ_o = 0,02 Ом, Δ_∞ = 20·106 Ом и γ_s = 0,5%.

Отсюда для любого х погрешность (в процентах) γ(х) = 100 [0,02/x + 0,5/100 + х/(20·106)].