Комбинационные цифровые устройства
Под комбинационным цифровым устройством (КЦУ) понимается цифровое устройство, обеспечивающее преоб-разование совокупности N входных цифровых сигналов в М выходных. При этом состояние выходных сигналов в данный момент времени определяется состоянием вход-ных сигналов в этот же момент времени. Т. е. КЦУ «не помнит» предыстории поступления сигналов на его вход. Правила функционирования КЦУ определяются реализуе-мыми ими функциями алгебры логики.
Реализация КЦУ предполагает выбор определенных ло-гических элементов из заданного набора и их соединение таким образом, чтобы обеспечивалась зависимость цифро-вых выходных сигналов от входных с заданными правила-ми функционирования.
При реализации КЦУ широко используются интеграль-ные комбинационные логические микросхемы малой сте-пени интеграции, образующие основу элементной базы цифровой электроники.
При выборе конкретной микросхемы необходимо руко-водствоваться видом реализуемой ею логической функ-ции, быстродействием, нагрузочной способностью и воз-можностью совместимости электрических характеристик входных и выходных сигналов с остальными элементами схемы.
Стандартные буквенные обозначения в маркировке ком-бинационных микросхем ТТЛ-, ЭСЛ- и КМОП-типов, оп-ределяющие выполняемые ими функции: ЛА обозначает функцию И - НЕ; ЛЕ – функцию ИЛИ - НЕ; ЛИ –функцию И; ЛЛ – функцию ИЛИ; ЛР – функцию И – ИЛИ – НЕ; ЛН – функцию НЕ; ЛП – функцию повторителя.
При формировании сигналов ТТЛ- или КМОП-уровней из аналогового сигнала, например из синусоиды, при об-работке сигналов в условиях большого уровня помех, а также в генераторах импульсов широкое применение наш-ли цифровые триггеры Шмитта. Характерной особенно-стью этих элементов является наличие гистерезиса на их передаточной характеристике.
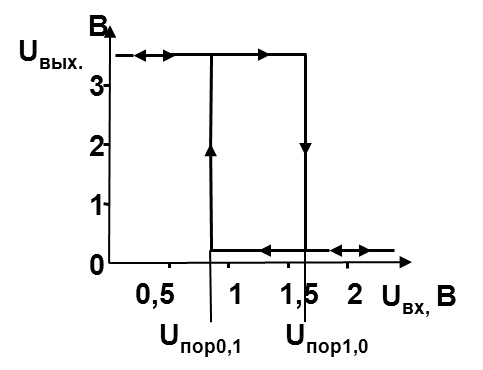При плавном изменении входного сигна-ла у триггера Шмита происходит скачко-образное изменение выходного, причем пороги срабатывания при переходе из нуля в единицу и из единицы в нуль от-личаются. Из рисунка видно, что уровни выходных напряжений логической единицы и логического нуля соответствуют стандартным ТТЛ
-уровням: Е0 ≈ 0,2В и Е1 ≈ 3,5В. Однако значение порого-вого напряжения, которое у ТТЛ –элементов Uпор ≈ 1,5В, отличается: у триггера Шмита оно имеет два значения Uпор1,0 ≈ 1,65В и Uпор0,1 ≈ 0,85В.
Лек14
В случаях, когда часть входов многовходовых элементов остается незадействованной, на неиспользованные входы этих элементов необходимо подавать логические нули или логические единицы в зависимости от логики выполняе-мой операции. Так, если неиспользуемыми являются отде-льные входы элемента И, то, чтобы результат операции не исказился, на них необходимо подавать напряжения логи-ческой единицы. Сделать это можно, подключив неиспо-льзуемые входы элемента И через ограничительный рези-стор к источнику питания. Если неиспользуемыми являю-тся входы элемента ИЛИ, то их необходимо подключить через ограничительный резистор к нулевому потенциалу общего провода, подав на них, таким образом, уровень на-пряжения логического нуля.
Если количества входов элемента недостаточно, то воз-можно наращивание входов схемы путем пирамидального объединения нескольких элементов. Применение подоб-ных структур, позволяющих на базе двух четырехвходо-вых элементов осуществить обработку восьми логических переменных для логического умножения и логического сложения, показано на рисунках:
Сумматоры.
Сумматоры – это класс КЦУ, выполняющих операцию математического сложения двух двоичных п-разрядных чисел. Сумматоры бывают полными и неполными.
Неполный сумматор (полусумматор) – представляет со-бой комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одно-разрядных чисел в соответствии с таблицей истинности:
А и В – входные одно-разрядные числа; S1 – выход суммы; Р1 – вы-ход переноса в стар-ший разряд.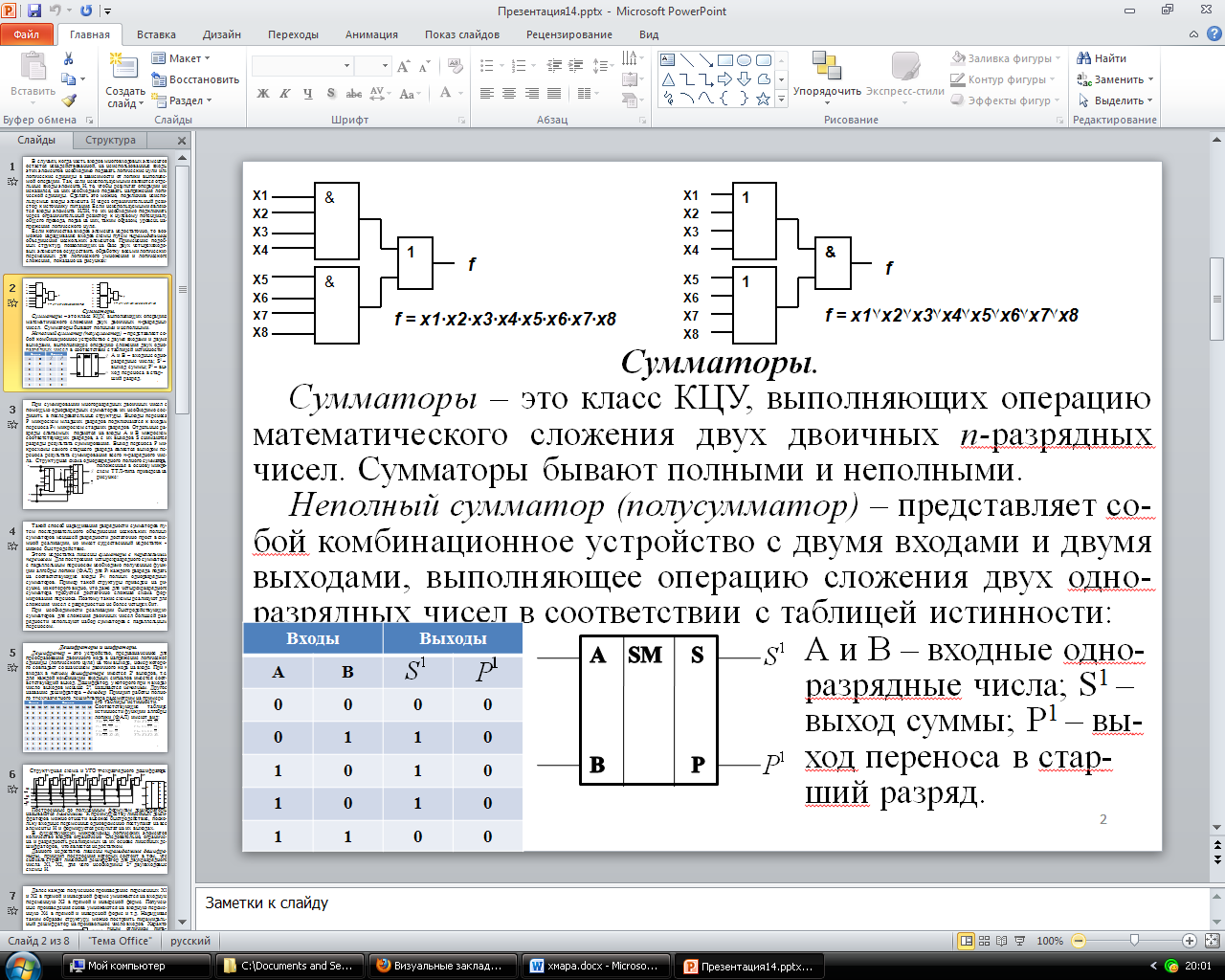 
При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их необходимо сое-динить в последовательные структуры. Выходы переноса Р микросхем младших разрядов подключаются к входам переноса Р-1 микросхем старших разрядов. Отдельные ра-зряды слагаемых подаются на входы А и В микросхем соответствующих разрядов, а с их выходов S снимаются разряды результата суммирования. Выход переноса Р ми-кросхемы самого старшего разряда является выходом пе-реноса результата суммирования всего п-разрядного чис-ла. Структурная схема одноразрядного полного сумматора,
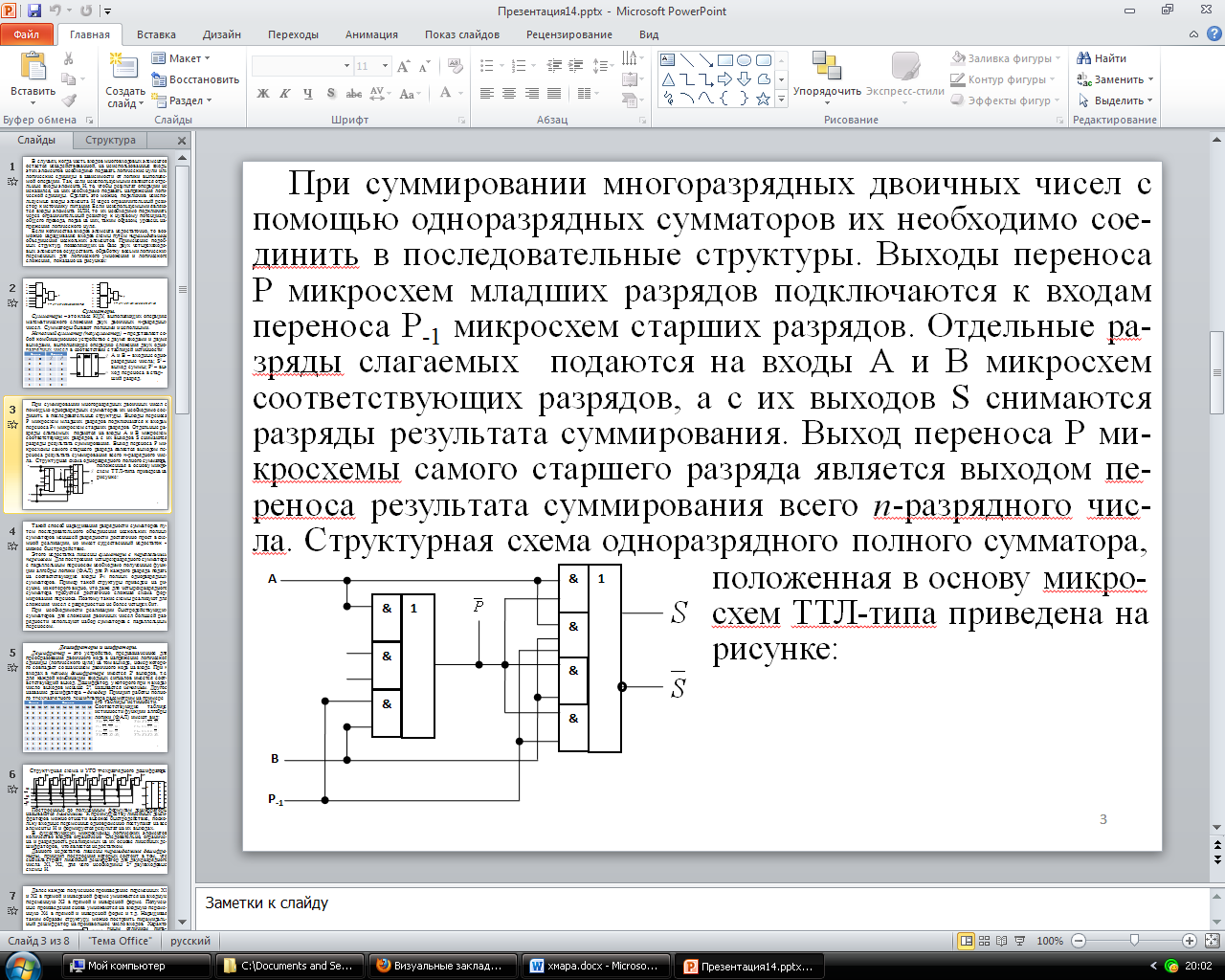положенная в основу микро-схем ТТЛ-типа приведена на рисунке:
Такой способ наращивания разрядности сумматоров пу-тем последовательного объединения нескольких полных сумматоров меньшей разрядности достаточно прост в схе-мной реализации, но имеет существенный недостаток – низкое быстродействие.
Этого недостатка лишены сумматоры с параллельным переносом. Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные функ-ции алгебры логики (ФАЛ) для Рi каждого разряда подать на соответствующие входы Р-1 полных одноразрядных сумматоров. Пример такой структуры приведен на ри-сунке, из которого видно, что даже для четырехразрядного сумматора требуется достаточно сложная схема фор-мирования переноса. Поэтому такие схемы реализуют для сложения чисел с разрядностью не более четырех бит.
При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей раз-рядности используют набор сумматоров с параллельным переносом.
Дешифраторы и шифраторы.
Дешифратор – это устройство, предназначенное для преобразования двоичного кода в напряжение логической единицы (логического нуля) на том выходе, номер которо-го совпадает со значением двоичного кода на входе. При п входах в полном дешифраторе имеется 2п выходов, т.е. для каждой комбинации входных сигналов имеется соот-ветствующий выход. Дешифратор, у которого при п входах число выходов меньше 2п, называется неполным. Другое название дешифратора – декодер. Принцип работы полно-го трехразрядного дешифратора рассмотрим на примере
его таблицы истинности.
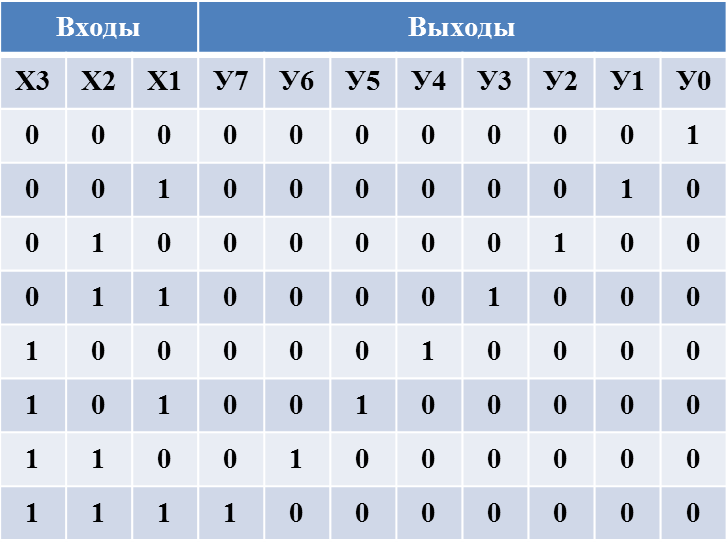Соответствующие таблице истинности функции алгебры логики (ФАЛ) имеют вид:
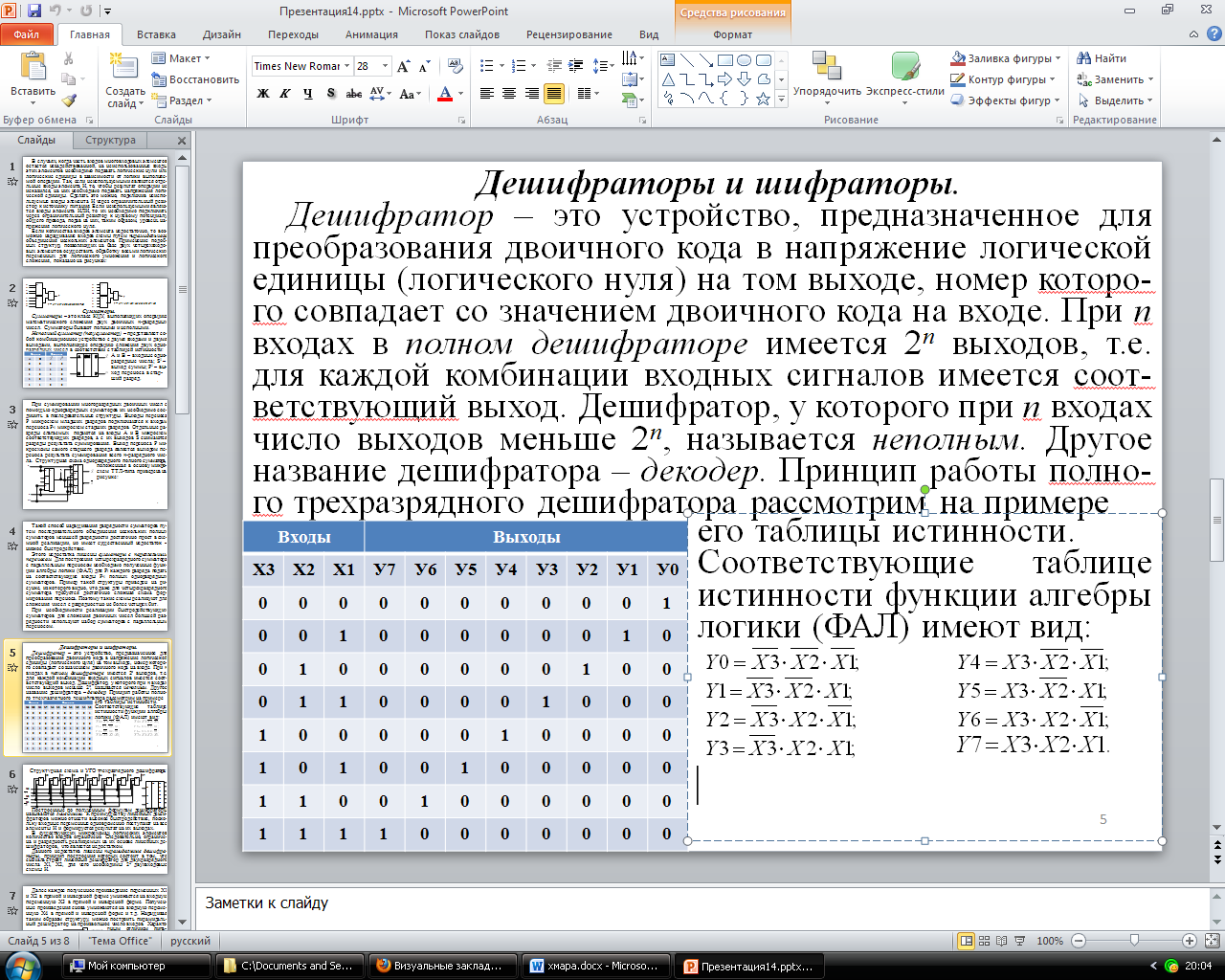
Структурная схема и УГО трехразрядного дешифратора:
Построенные по полученным формулам дешифраторы называются линейными. К преимуществу линейных деши-фраторов можно отнести высокое быстродействие, поско-льку входные переменные одновременно поступают на все элементы И и формируется результат на их выходах.
В существующих микросхемах логических элементов количество входов ограничено. Следовательно, ограниче-на и разрядность реализуемых на их основе линейных де-шифраторов, что является недостатком.
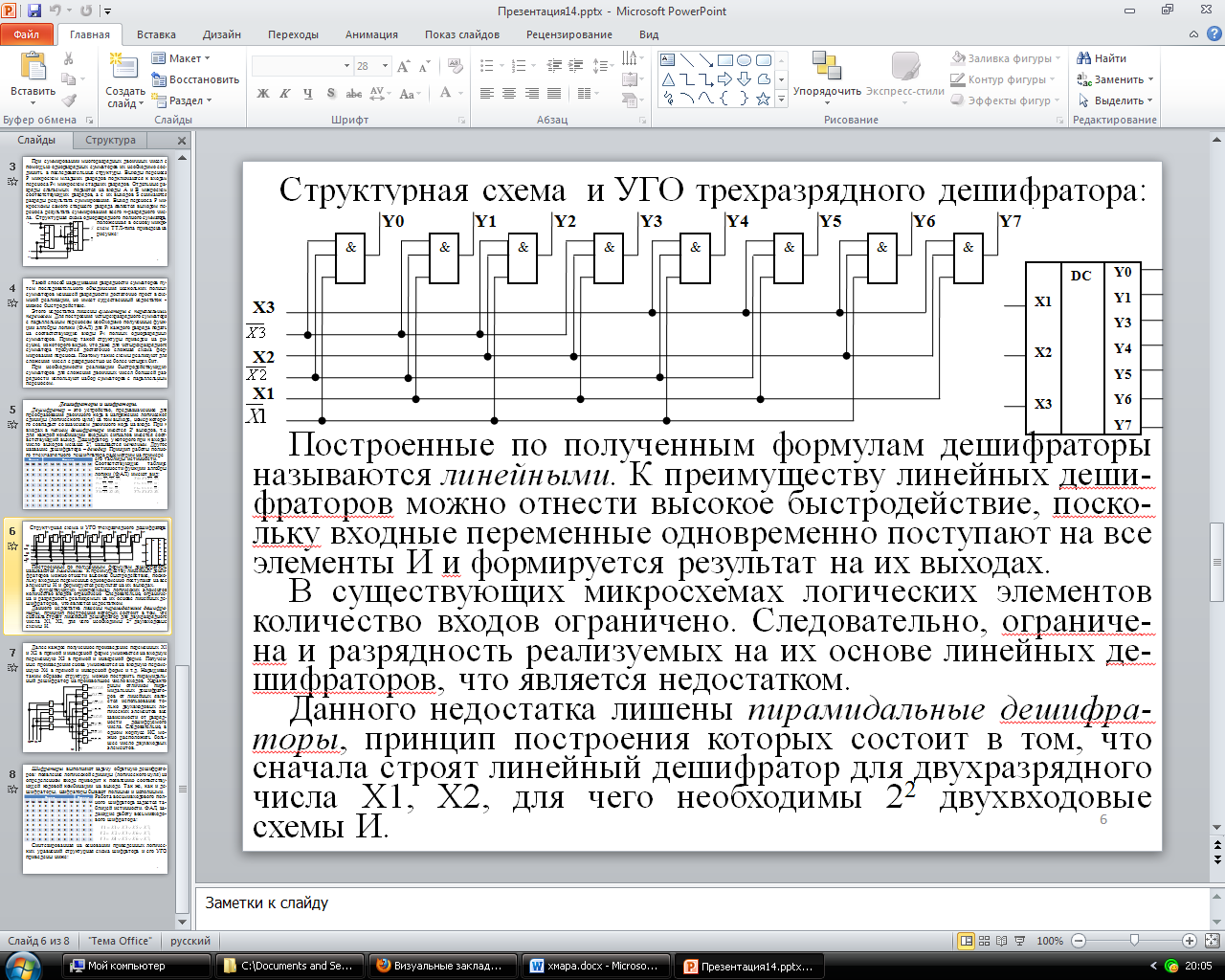
Данного недостатка лишены пирамидальные дешифра-торы, принцип построения которых состоит в том, что сначала строят линейный дешифратор для двухразрядного числа Х1, Х2, для чего необходимы 22 двухвходовые схемы И.
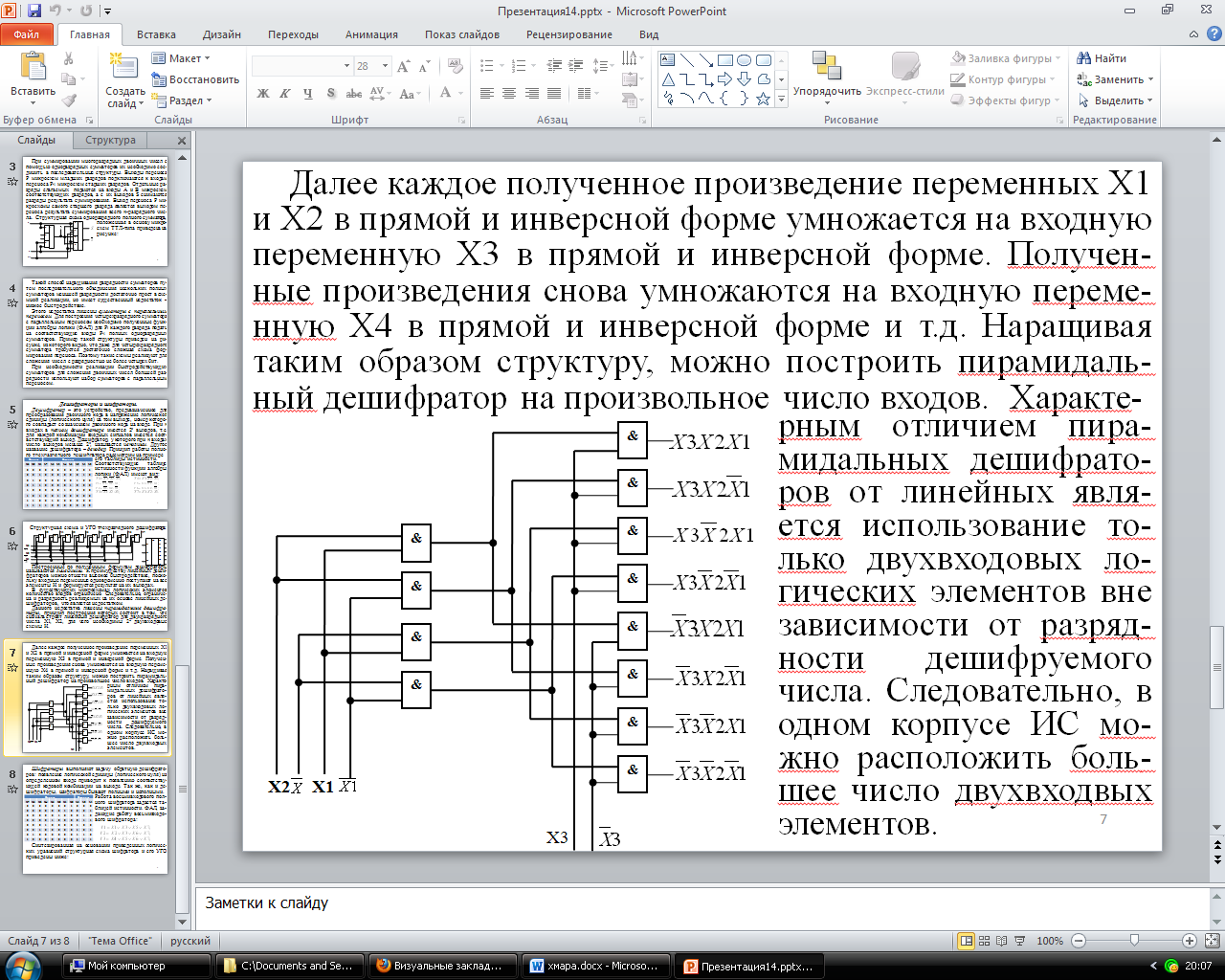
Далее каждое полученное произведение переменных Х1 и Х2 в прямой и инверсной форме умножается на входную переменную Х3 в прямой и инверсной форме. Получен-ные произведения снова умножаются на входную переме-нную Х4 в прямой и инверсной форме и т.д. Наращивая таким образом структуру, можно построить пирамидаль-ный дешифратор на произвольное число входов. Характерным отличием пира-мидальных дешифрато-ров от линейных явля-ется использование то-лько двухвходовых ло-гических элементов вне зависимости от разряд-ности дешифруемого числа. Следовательно, в одном корпусе ИС мо-жно расположить боль-шее число двухвходвых элементов.
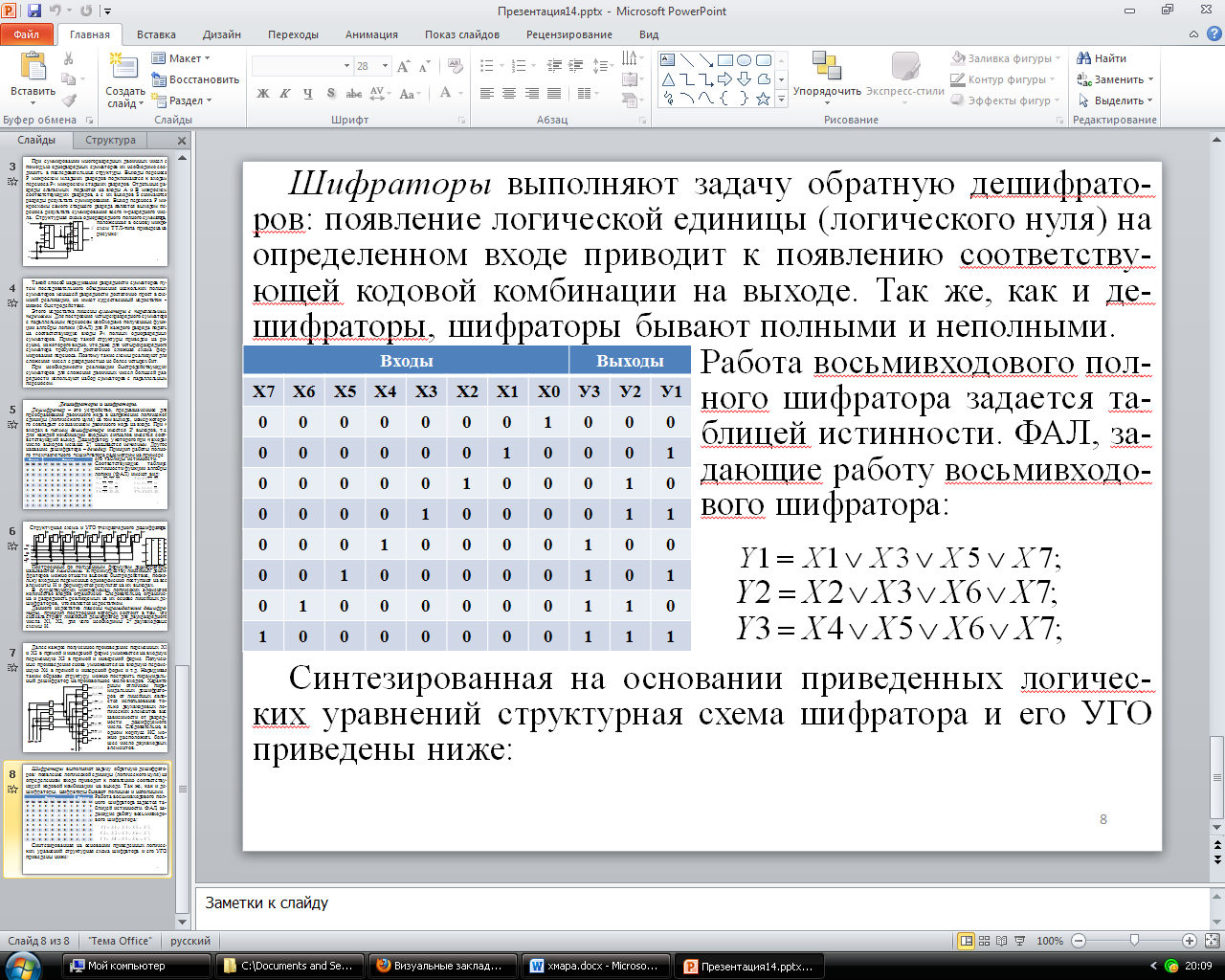
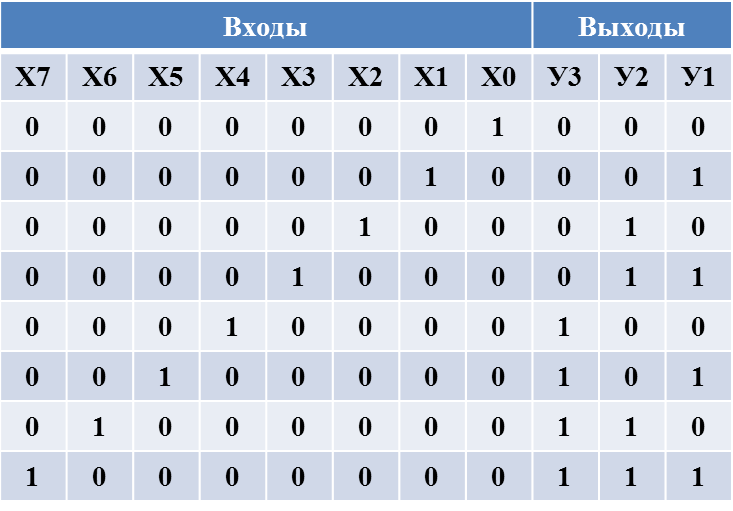-Шифраторы выполняют задачу обратную дешифрато-ров: появление логической единицы (логического нуля) на определенном входе приводит к появлению соответству-ющей кодовой комбинации на выходе. Так же, как и де-шифраторы, шифраторы бывают полными и неполными.
Работа восьмивходового пол-ного шифратора задается та-блицей истинности. ФАЛ, за-дающие работу восьмивходо-вого шифратора:
Синтезированная на основании приведенных логичес-ких уравнений структурная схема шифратора и его УГО приведены ниже: