Методы структурного синтеза и языки описания цифровых автоматов
Введение в теорию автоматов и структурный синтез цифровых автоматов
СОДЕРЖАНИЕ
1 Основные понятия и определения
2. Методы структурного синтеза и языки описания цифровых автоматов
3. Элементарный автомат (триггерный элемент)
4. Синтез цифрового автомата с памятью
Введение
Создание современных автоматизированных средств и систем управления основывается на следующих двух научных направлениях: теории преобразования информации и теории построения различного рода преобразователей информации.
Первое направление включает в себя общую теорию алгоритмов, абстрактную теорию автоматов. В нем рассматриваются общие вопросы формализации процессов обработки информации.
Второе направление включает в себя элементы математической логики, структурную теорию автоматов. В нем рассматриваются принципы и методы построения автоматов, которые реализуют алгоритмы обработки информации, полученные на этапе абстрактного синтеза автоматов.
В соответствии с этими направлениями в теории автоматов выделяют два больших раздела: абстрактную теорию автоматов и структурную теорию автоматов.
Основные понятия и определения
Термин «автомат», как правило, используется в двух аспектах. С одной стороны, автомат - это устройство, выполняющее некоторые функции без непосредственного участия человека. В этом смысле мы говорим, что ЭВМ – автомат, так как после загрузки программы и исходных данных ЭВМ решает заданную задачу без участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов. В этом смысле автомат представляется как «черный ящик», имеющий конечное число входов и выходов и некоторое множество внутренних состояний Q = {q1(t), q2(t), ..., qn(t)}, в которые он под действием входных сигналов переходит скачкообразно, т. е. практически мгновенно, минуя промежуточное состояние. Конечно, это условие не выполняется в реальности, так как любой переходный процесс длится конечное время.
Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов – конечные множества.
На практике часто используется понятие цифрового автомата, под которым понимают устройство, предназначенное для преобразования информации. С общей точки зрения, процесс получения информации есть ни что иное, как процесс снятия неопределенности в результате того, что из некоторой совокупности возможных в данной конкретной ситуации явлений выделяется явление, фактически имевшее место.
Таким образом, в понятии информации существенно не само происшедшее явление, а лишь его отношение к совокупности явлений, которые могли произойти.
Устройства, служащие для преобразования дискретной информации, называются дискретными автоматами.
В современных дискретных автоматах принято обычно отождествлять буквы используемого стандартного алфавита с цифрами той или иной системы счисления.
В состав цифровых автоматов обязательно входят запоминающие элементы (элементы памяти). Выходные сигналы в таких автоматах формируются в зависимости от входных сигналов и состояний, в которых находятся элементы памяти. Поэтому дискретные автоматы принято называть также цифровыми автоматами.
Основным качеством, выделяющим дискретные автоматы из числа всех других преобразователей информации, является наличие дискретного множества внутренних состояний и свойства скачкообразного перехода автомата из одного состояния в другое. Скачкообразность перехода означает возможность трактовать этот переход как мгновенный, хотя для любого реально существующего автомата имеет место конечная длительность переходных процессов, так что требование скачкообразности перехода не удовлетворяется.
Второе допущение состоит в том, что после перехода автомата в произвольное состояние переход в следующее состояние оказывается возможным не ранее, чем через некоторый фиксированный для данного автомата промежуток времени τ > 0, так называемый интервал дискретности автомата. Это допущение дает возможность рассматривать функционирование цифрового автомата в дискретном времени. При построении автоматов с дискретным автоматным временем различают синхронные и асинхронные автоматы.
В синхронных автоматах моменты времени, в которые оказывается возможным изменение состояния автомата, определяются специальным устройством – генератором синхронизирующих импульсов. Соседние моменты времени оказываются при этом обычно разделенными равными временными промежутками.
В асинхронных автоматах моменты переходов из одного состояния в другое заранее не определены и могут совершаться через неравные между собой промежутки времени.
Изменения состояний цифрового автомата вызываются входными сигналами, которые возникают вне автомата и передаются в автомат по конечному числу входных каналов. В отношении входных сигналов цифровых автоматов принимаются два допущения: во-первых, для любого цифрового автомата число различных входных сигналов обязательно конечно, а, во-вторых, входные сигналы рассматриваются как причина перехода автомата из одного состояния в другое и относятся к моментам времени, определяемым соответствующими им переходами.
Отметим, что при таком допущении входной сигнал рассматривается как мгновенный, хотя в действительности он имеет конечную длительность. Особо следует подчеркнуть, что реальный физический входной сигнал, вызывающий изменение состояния автомата в момент времени t, может кончиться до наступления этого момента, однако, тем не менее, он относится именно к текущему моменту времени t, а не к предыдущему (t –1).
Результатом работы цифрового автомата является выдача выходных сигналов, передаваемых из автомата во внешние цепи по конечному числу выходных каналов.
В отношении выходных сигналов вводятся допущения, аналогичные допущениям для входных сигналов. Во-первых, число различных выходных сигналов для любого цифрового автомата всегда конечно. Во-вторых, каждому отличному от нуля моменту автоматного времени относится соответствующий ему входной сигнал. Реальный физический выходной сигнал y(t), отнесенный к моменту времени t, появляется всегда после соответствующего этому же моменту времени входного сигнала x(t). Что же касается момента времени t перехода автомата из состояния q(t–1) в состояние q(t), то сигнал y(t) может фактически появится либо раньше, либо позже этого момента.
В первом случае принимается, что выходной сигнал y(t) однозначно определяется входным сигналом x(t) и состоянием q(t–1) автомата в предыдущий момент времени, во втором случае сигнал y(t) однозначно определяется парой (x(t), q(t)). Будем считать, что для любого момента времени всегда имеет место лишь одна из этих возможностей (одновременно для всех переходов).
Цифровые автоматы, в которых выходной сигнал y(t) определяется парой
(x(t), q(t – 1)), будем называть автоматами первого рода, а автоматы, в которых сигнал y(t) определяется парой (x(t), q(t)), – автоматами второго рода.
Цифровой автомат (первого или второго рода) называется правильным, если выходной сигнал y(t) определяется одним лишь его состоянием (q(t –1) или q(t)) и не зависит явно от входного сигнала x(t).
Автоматы первого рода обычно называют автоматами Мили, а автоматы второго рода – автоматами Мура.
Общая теория автоматов при сделанных выше допущениях разбивается на две большие части, которым присвоены названия абстрактной теории автоматов и структурной теории автоматов. Различие между ними заключается в том, что в абстрактной теории не учитываются структура как самого автомата, так и структуры его входных и выходных сигналов. Входные и выходные сигналы рассматриваются при этом просто как буквы двух фиксированных для данного автомата алфавитов: входного и выходного. Не интересуясь способом построения автомата, абстрактная теория изучает лишь те переходы, которые претерпевает автомат под воздействием входных сигналов, и те выходные сигналы, которые он при этом выдает.
В противоположность абстрактной теории, структурная теория автоматов учитывает структуры автомата и его входных и выходных сигналов. В структурной теории изучаются способы построения автоматов из нескольких элементарных автоматов, способы кодирования входных и выходных сигналов элементарными сигналами, передаваемыми по реальным входным и выходным каналам.
Таким образом, структурная теория автоматов является продолжением и дальнейшим развитием абстрактной теории. В частности, задача синтеза идеализированного (без учета переходных процессов) цифрового автомата естественным образом подразделяется на этапы абстрактного и структурного синтеза.
Частным случаем дискретных автоматов являются автоматы, обладающие лишь одним внутренним состоянием. Такие автоматы называются комбинационными схемами или автоматами без памяти. Работа таких автоматов состоит в том, что они сопоставляют каждому входному сигналу x(t) выходной сигнал y(t).
Для задания конечного автомата фиксируются три конечных множества (алфавита):
- множество возможных входных сигналов:
X = {x1, x2, ..., xm};
- множество возможных выходных сигналов:
Y = {y1, y2, ..., yk};
- множество возможных внутренних состояний автомата:
A = {a0, a1, ..., an}.
На этих множествах задают два логических оператора:
- функцию переходов f, определяющую состояние автомата a(t + 1) в момент дискретного времени t + 1 в зависимости от состояния автомата a(t) и значения входного сигнала x(t) в момент времени t:
a(t + 1) = f[a(t), x(t)]; (1)
- функцию выходов, определяющую зависимость выходного сигнала автомата y(t) от состояния автомата a(t) и входного сигнала x(t) в момент времени t:
y(t) = [a(t), x(t)]. (2)
Кроме того, на множестве состояний автомата фиксируют одно из внутренних состояний а0 в качестве начального состояния.
Понятие состояние автомата используется для описания систем, выходные сигналы которых зависят не только от входных сигналов в данный момент времени, но и от некоторой предыстории, т.е. сигналов, которые поступали на входы системы ранее. Следовательно, цифровые автоматы относятся к последовательностным схемам, которые, как уже отмечалось, обладают памятью. Понятие состояние автомата соответствует некоторой памяти о прошлом, поэтому ввод этого понятия позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.
Работу абстрактного автомата следует рассматривать применительно к конкретным интервалам времени, т.к. каждому интервалу дискретности t будет соответствовать свой выходной сигнал y(t). Следовательно, функционирование автомата рассматривается через дискретные интервалы времени конечной продолжительности. В абстрактной теории цифровых автоматов считается, что входные сигналы воздействуют на синхронный автомат в момент начала каждого i-того интервала (кванта) времени, выделенного соответствующим синхроимпульсом (тактом), а изменение внутренних состояний автомата происходит в интервалы времени между смежными синхроимпульсами, когда нет воздействия входных сигналов.
Операторы, описывающие работу автомата, обычно задают таблицей переходов и таблицей выходов.
В таблице переходов показывают в какое состояние попадает автомат от того или иного входного сигнала. В таблице выходов показывают какой выходной сигнал генерирует автомат в зависимости от типа входного сигнала и текущего состояния автомата.
К примеру, рассмотрим таблицы переходов и выходов некоторого автомата.
Таблица переходов автомата
Входной Состояние
сигнал a0 a1 a2 a3
x1 a1 a2 a3 a3
x2 a0 a0 a0 a0
Таблица выходов автомата
Входной Состояние
сигнал a0 a1 a2 a3
x1 y2 y2 y1 y2
x2 y2 y2 y2 y3
В клетку таблицы переходов, находящуюся на пересечении столбца с буквой аi и строки с буквой xj, записывается состояние автомата, в которое он переходит из состояния аi при подаче на вход сигнала xj. В аналогичную клетку таблицы выходов записывается выходной сигнал yi, который формируется автоматом при таком переходе.
Операторы переходов и выходов могут быть заданы одной таблицей, по которой однозначно определяются переходы и выходы автомата.
Таблица переходов и выходов автомата
| Выходной сигнал | Состояние | |||
| a0 | a1 | a2 | a3 | |
| x1 | a1 y2 | a2 y2 | a3 y1 | a3 y2 |
| x2 | a0 y2 | a0 y2 | a0 y2 | a0 y3 |
Большую наглядность обеспечивает задание конечных автоматов с помощью графов илидиаграмм состояний.
Граф автомата состоит из узлов, соединенных ветвями. Узлы (кружки на схеме графа) отождествляют внутренние состояния автомата. Каждая ветвь графа, т.е. ориентированная линия, стрелка которой указывает следующее состояние автомата, отмечается входным сигналом, вызывающим в автомате соответствующий данной ветви переход, и выходным сигналом, который возникает при этом переходе. Входной и соответствующий ему выходной сигналы разделяются на чертеже запятой или косой чертой. Если некоторый входной сигнал не меняет состояния автомата, то соответствующая ветвь замыкается на кружке (узле), из которого она выходит.
Поскольку таблица состояний и граф (диаграмма) состояний несут одну и ту же информацию, их можно преобразовать друг в друга. Каждое состояние представляется кружком, а каждый элемент таблицы преобразуется в отрезок ориентированной линии, соединяющей соответствующие кружки. Процедура обратного преобразования очевидна.
В настоящее время в классе синхронных автоматов рассматривают, в основном, два типа автоматов: автомат Мили и автомат Мура.
Граф автомата Мили, заданного вышеприведенными таблицами, отражен на рис.1. Закон функционирования автоматов Мили может быть задан следующим образом:
a(t + 1) = f[a(t), x(t)];
y(t) = [a(t), x(t)],
где t = 1, 2, .....
Отличительная особенность автоматов Мили состоит в том, что их выходные сигналы в некоторый момент времени не зависят как от состояния автомата, так и от значения входного сигнала в этот же момент времени.
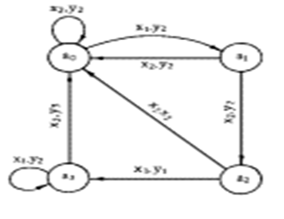
Рис1. Граф автомата Мили.
У автоматов Мура выходные сигналы в момент времени t однозначно определяются состоянием автомата в этот же момент времени и в явном виде не зависят от значения входных сигналов xi(t).
Функции переходов и выходов автомата Мура, заданного на множестве входных сигналов X, множестве внутренних состояний A = {a0, a1, ,an} и множестве выходных сигналов Y, можно записать в виде
a(t + 1) = f[a(t), x(t)], (3)
y(t) = [a(t)]. (4)
эти операторы удобно задавать отмеченнойтаблицей переходов.
Такие таблицы строятся так же, как и таблицы переходов автомата Мили, но над символами каждого внутреннего состояния записываются выходные сигналы, которые выдает автомат в данном состоянии.
Отмеченная таблица переходов автомата
Выходной сигнал
y2 y2 y2 y1 y2 y3
Входной Состояние
сигнал a0 a1 a2 a3 a4 a5
x1 a1 a2 a3 a4 a4 a1
x2 a0 a0 a0 a5 a5 a0
Граф автомата Мура, заданного этой таблицей, приведен на рис. 2. На этом рисунке состояния автомата обозначаются символами bi.
На графах автомата Мура значения выходных сигналов записываются около узлов.
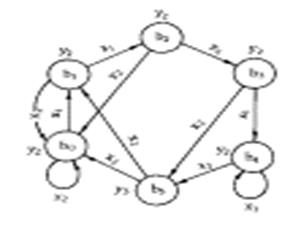
Рис. 2. Автомат Мура.
Между автоматами Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой или обратно. Автомат Мура можно рассматривать как частный случай автомата Мили, имея в виду, что последовательность состояний выходов автомата Мили опережает на один такт последовательность состояний выходов автомата Мура, т.е. различие между автоматами Мили и Мура состоит в том, что в автоматах Мили состояние выхода возникает одновременно с вызывающим его состоянием входа, а в автоматах Мура - с задержкой на один такт, т.к в автоматах Мура входные сигналы изменяют только состояние автомата.
Помимо автоматов Мили и Мура выделяют еще, так называемый, совмещенный
Методы структурного синтеза и языки описания цифровых автоматов
В зависимости от способа задания функций переходов и выходов (f и ) в настоящее время выделяют два класса языков описания цифровых автоматов - начальные языки и стандартные, или автоматные языки. В начальных языках автомат описывается на поведенческом уровне, т.е. функции переходов и выходов обычно в явном виде не заданы. Среди начальных языков следует выделить язык регулярных выражений алгебры событий, язык логических схем алгоритмов, язык граф-схем алгоритмов. Принципы построения граф-схем алгоритмов подробно описаны в Глава 11, там же рассматриваются некоторые возможные содержательные термины, которые обычно используются при описании алгоритмов.
Среди автоматных языков наиболее распространены таблицы переходов и выходов, а также графы, которые мы рассматривали ранее.
Используются также, так называемые, кодированные таблицы переходов и выходов, в которых определяется зависимость значений в двоичном коде внутренних состояний и выходных сигналов от значений в этом же коде входных сигналов и внутренних состояний элементарных автоматов в предыдущий момент времени.
Задача синтеза конечных автоматов заключается в построении сложного автомата из более простых автоматов, называемых элементарными автоматами. На практике в большинстве случаев применяют элементарные автоматы с двумя внутренними устойчивыми состояниями, которые соединяются между собой с помощью логических элементов таким способом, чтобы обеспечить функционирование схемы в соответствии с заданными кодированными таблицами переходов и выходов.
Для синтеза конечных автоматов необходимо прежде всего выбрать систему элементов, из которых должны строиться заданные автоматы. В большинстве схем цифровых автоматов в качестве элементов памяти применяются элементарные автоматы, имеющие следующие особенности.
1.Элементарные автоматы, например триггера, являются автоматами Мура и имеют два внутренних устойчивых состояния.
2. Двум внутренним состояниям элементарного автомата соответствуют два различных выходных сигнала, которые по существу и позволяют физически различать состояния элементарных автоматов.
3. В общем случае элементарные автоматы могут иметь несколько физических входов.
Для того чтобы можно было построить схему любого конечного автомата, набор элементов, с помощью которых проводится синтез автомата, должен быть функционально полным и включать в себя в качестве элементарных автоматов триггера, т.е, необходимо и достаточно, чтобы он содержал:
- хотя бы один элементарный автомат с двумя различными состояниями, для которых соблюдаются условия полноты системы переходов и выходов;
- логические элементы, образующие функционально полную систему для синтеза логических комбинационных схем.
Напомним, что набор логических элементов будет функционально полным, если из элементов этого набора можно построить любую логическую схему компьютера.
Приведем пример общей структурной модели последовательностной схемы, содержащей триггера.
X Z
Q Y
Рис. 4.
При решении задач анализа и синтеза последовательностных схем обычно разделяют последовательностную схему на элементы памяти и комбинационную часть.
В самом общем виде последовательность структурного синтеза последовательностного цифрового автомата можно представить следующим образом.
В начале в четкой словесной форме формулируется исходное задание проекта. В зависимости от типа и сложности проектируемого цифрового автомата последующий этап синтеза может быть различным.
Возможен вариант, когда можно сразу приступать к формированию в аналитической форме системы рекуррентных логических функций. Далее выбирается в зависимости от физического типа элементов функционально полный набор логических элементов (базис) и соответствующая этому набору система логических функций. Затем рекуррентные логические функции представляются через логические функции выбранной функционально полной системы и минимизируются в соответствии с выбранными критериями. Этот этап синтеза обычно называют комбинационным синтезом.
Задачи комбинационного синтеза последовательностных цифровых автоматов полностью совпадают с задачами синтеза комбинационных логических схем.
На этом же этапе разработок строится содержательная граф-схема алгоритма функционирования автомата. Далее формируются необходимые кодированные таблицы переходов и выходов и при необходимости строится граф автомата (диаграмма состояний).
Возможен вариант, когда вместо формирования системы рекуррентных функций в начале составляют некоторый предварительный упрощенный вариант граф-схемы (возможно содержательной) автомата или граф автомата, т.е. диаграммы состояний, и предварительный вариант кодированной таблицы состояний. И только после этого формируется система рекуррентных функций, и выполняются все упомянутые последующие процедуры с поэтапным уточнением граф-схемы автомата, диаграммы его состояний и кодированных таблиц состояний (выходов, переходов и т.д.).
Далее, ориентируясь на сформированные таблицы и граф-схему, проектируется логическая схема цифрового автомата, в которой используются логические элементы выбранного базиса. Эта схема представляется как структурная или функциональная. После ее разработки можно приступать к созданию принципиальной схемы разрабатываемого последовательностного цифрового автомата.
Надо учесть, что в общем случае процедура синтеза цифрового автомата плохо формализуема и в значительной мере зависит от опыта разработчика.
Элементарный автомат (триггерный элемент)
Как уже отмечалось, наиболее типичным примером элементарного автомата и основным последовательностным Элементом является триггер. Термин "триггер" используется для электронных цифровых схем, обладающих двумя устойчивыми внутренними состояниями, которые они могут хранить неограниченно долго, во всяком случае до следующего такта.
Триггер имеет два выходных сигнала Q и Q. Сигнал Q считается истинным или прямым, а сигнал Q - дополнительным или инверсным. Этим сигналам соответствует один из двух уровней напряжения: L или H, и они дополняют друг друга. Выходные сигналы триггера постоянны до тех пор, пока они не будут изменены под воздействием входных сигналов, т.е. триггер имеет два устойчивых состояния (режима): Q = H иQ = L или Q = L и Q = H. Первое из них когда Q = H называется состоянием установки, а второе - состоянием сброса. Предположим, что для триггера используется положительная логика. Тогда состояниям установки и сброса ставятся в соответствие логические состояния 1 и 0.
Существуют различного типа триггерные схемы, в частности, типа: D, T, RS, JK. Для каждого из них имеется однозначное соответствие между входными сигналами и соответствующими переходами состояний триггера. Это соответствие задается таблицей состояний. Приведем, например, условное обозначение RS триггера и его таблицу состояний.
S Q
R Q
Рис. 5 Таблица состояний RS триггера
Входы
Текущее состояние S = L R = L S = L R = H S = H R = L S = H R = H
Выходы Q = L Q = H L H L H H L Не определено
Триггер оказывается в состоянии установки, если на вход S подается сигнал высокого уровня, и в состоянии сброса, когда сигнал высокого уровня подается на вход R. Если на оба входа триггера подаются сигналы низкого уровня, то его состояние не меняется, но если на оба входа подаются сигналы высокого уровня, то состояние триггера будет неопределенным.
Логическое поведение триггера, как любого другого автомата, описывается логическими таблицами состояний и переходов. Приведем такие таблицы для RS триггера.
Таблица состояний
Входы S R
Текущее 00 01 10 11
состояние Выходы
Q = 0 Q = 1 01 00 11 Не определено
Таблица переходов
| Текущее состояние Q | Следующее состояние Q | S | R |
| d | |||
| d |
где d - недоопределенное состояние, т.е. в может равняться либо 0, либо 1.
Приведем вариант реализации RS-триггера на элементах И-НЕ:
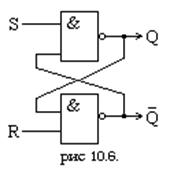
В схеме с N триггерами (например регистр с N триггерами) состояния характеризуются N-разрядным двоичным словом, каждый разряд которого ассоциируется с одним из триггеров. Так как существует 2N различных комбинаций N-разрядного слова, то у данной схемы имеются 2N устойчивых состояний. Очевидно, что состояние выходных сигналов такого регистра зависит не только от того на какие его входы поступили сигналы, но и от того в каком состоянии были его триггера до прихода входных сигналов. Это и является отличительной чертой последовательностных схем от схем первого рода - комбинационных логических схем.
Обычный Т-триггер имеет один счетный вход Т и как все триггера два выхода: Q и Q. Он переключается только при изменении входного сигнала Т с значения 0 на 1.
Синхронизируемый Т-триггер имеет кроме счетного входа Т еще вход СК для синхронизирующего сигнала (синхроимпульса) СИ. Опрокидование триггера происходит в том случае, когда в момент прихода СИ Т = 1, если
T = 0, то СИ не оказывает воздействия на триггер.
