Нормирование погрешностей и классы точности средств измерений

Средства измерений можно использовать только тогда, когда известны их метрологические характеристики. Обычно указываются номинальные значения параметров средств измерений и допускаемые отклонения от них. Сведения о метрологических характеристиках приводятся в технической документации на средства измерений или указываются на них самих. Как правило, реальные метрологические характеристики имеют отклонения от их номинальных значений. Поэтому устанавливают границы для отклонений реальных метрологических характеристик от номинальных значений – нормируют их.
Нормирование метрологических характеристик средств измерений обеспечивает:

- предварительный расчет погрешностей результатов технических измерений (до проведения измерений);

-выбор средств измерений по заданным характеристикам их погрешностей.

Нормирование характеристик средств измерений проводится в соответствии с ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений». Соответствие средств измерений установленным для них нормам делает эти средства взаимозаменяемыми.

Погрешность средства измерения является только одной из составляющих погрешности результата измерений, получаемого с использованием данного средства измерения наряду с погрешностью метода измерений и погрешностью оператора, проводящего измерения.

Погрешности средств измерений нормируются в соответствии с ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования ».

В основе нормирования погрешностей средств измерений лежат следующие основные положения:

- В качестве норм указывают пределы допускаемых погрешностей, включающие в себя систематические и случайные составляющие.

- Под пределом допускаемой погрешности понимается наибольшее значение погрешности средства измерений, при котором оно еще признается годным к применению. Отдельно нормируют основную погрешность средства измерения, дополнительные погрешности и другие свойства, влияющие на точность измерений. При выполнении данного требования обеспечивается максимальная однородность средств измерений одного типа, то есть близкие значения дополнительных погрешностей, обусловленных одними и теми же факторами. Это дает возможность заменять один прибор другим однотипным без возможного увеличения суммарной погрешности. Пределы допускаемых погрешностей средств измерения применяются как для абсолютной, так и для относительной погрешности.

Пределы допускаемой абсолютной погрешности устанавливают как

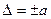(для аддитивной погрешности)

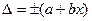(для мультипликативной погрешности), где 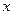– показание измерительного прибора, а и b – положительные числа, не зависящие от х.

Предел допускаемой относительной погрешности (в относительных единицах) для аддитивной погрешности устанавливают как

,

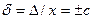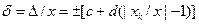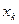а для мультипликативной - , где - конечное значение диапазона измерений прибора; c и d - относительные величины.

Пределы допускаемой приведенной погрешности устанавливают как

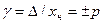, где 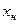– нормирующее значение; р - положительное число из ряда 1; 1,5; 2; 2,5; 4; 5; 6, умноженное на 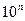( n = 1, 0, -1, -2 и т.д.). Нормирующее значение принимается равным конечному значению шкалы (если 0 находится на краю шкалы), сумме конечных значений шкалы (если 0 внутри шкалы), номинальному значению измеряемой величины, длине шкалы.

Класс точности средства измерения – обобщенная характеристика данного типа средства измерения, отражающая уровень точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств в технической документации на средство измерения. Примеры обозначения классов точности для различных форм выражения погрешности приведены в табл. 4.6.

Систематическаяпогрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Таблица 4.6

Обозначение классов точности

Пределы допускаемой основной погрешности	Обозначения	Форма выражения погрешности
в документации	на приборе
γ = ± 0,015	Класс точности 1,5	1,5	Приведенная погрешность
γ = ± 0,015	Класс точности 1,5	√1,5	Приведенная погрешность одинакова на всей шкале
δ = ± 0,005	Класс точности 0,5		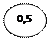Относительная погрешность, постоянная
δ = ± [ 0,0002 + 0,0001( xk/x –1)]	Класс точности 0,02/0,01	0,02/0,01	Относительная погрешность, возрастает с уменьшением х
Точность выше, чем меньше цифра и буква ближе к началу алфавита			Римские цифры или буквы латинского алфавита
			Таблица, график, функция

Пример Амперметр с диапазоном измерения ±25А, класс точности указан как 0,02/0,01, показывает 25 А. Чему равна сила тока?

δ = ± [ 0,0002 + 0,0001( x_k/x –1)] = ± [ 0,0002 + 0,0001( 50/25 –1)]= 0,03%

.

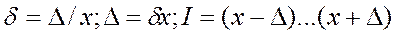I=24,992…25,008 A.

Класс точности не позволяет определить точность конкретного измерения, а лишь указывает пределы, в которых находится значение измеряемой величины.

2.3.5. Метрологическая надежность средств измерения

Метрологическая надежность средств измерения – способность средства измерения сохранять установленные значения метрологических характеристик при нормальных условиях измерения и рабочих условиях эксплуатации в течение определенного времени.

В процессе работы могут возникать неисправности, поломки. Вероятность возникновения внезапных отказов подчиняется экспоненциальному закону.

Интенсивность отказов – количество отказов в единицу времени 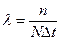, n – число отказов, N – число однотипных элементов.

Вероятность безотказной работы средства измерения

.

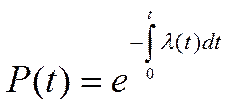Среднее время безотказной работы .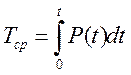

Если интенсивность отказов не меняется в течение заданного времени: .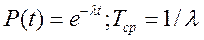

Пример: Измерительный преобразователь состоит из:

4 транзисторов ( );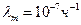

8 резисторов ( ;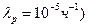

6 керамических сопротивлений ( ).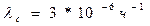

Определить вероятность внезапного отказа за 1000 часов работы.

Суммарная интенсивность отказов .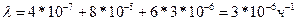

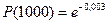- вероятность безотказн.работы. Вероятность отказа .

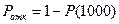Внезапные отказы являются явными, диагностика постепенных отказов из-за старения, износов и т.д. сложнее.

Исходя из требований метрологической надежности устанавливают межповерочные интервалы.

Пусть метрологическая характеристика средства измерения z подчиняется нормальному закону распределения в определенные моменты времени:

.

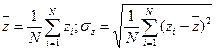В течение времени изменение статистических параметров метрологических характеристик описывается линейной функцией

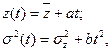
где 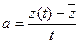,b - коэффициенты, зависящие от интенсивности износа и старения элементов и узлов средства измерения, определяются экспериментально.

Если коэффициенты также подчиняются нормальному закону, то

.

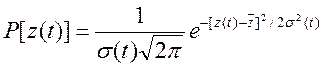Задавая вероятность безотказной работы, можно установить время, в течение которого она обеспечивается и назначить межповерочный интервал. На практике межповерочный интервал определяют как 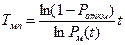, 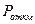- вероятность отказа за время между поверками;

- при технических измерениях: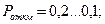

- при передаче информации: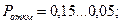

- при особо точных измерениях: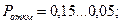

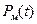- вероятность безотказной работы.

Пример. По техническим условиям вероятность безотказной работы прибора

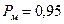в течение 2000 ч. Каким должен быть межповерочный интервал ?

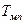Технические измерения предполагают 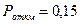, тогда 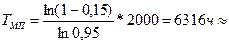9 мес.

Пример.- По истечении 9 месяцев эксплуатации из N=85 поверенных приборов два (m=2) забракованы

по результатам поверки. Должен ли быть откорректирован ?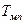

Можно воспользоваться номограммами, учитывающими различные варианты сочетаний вероятностей отказов.

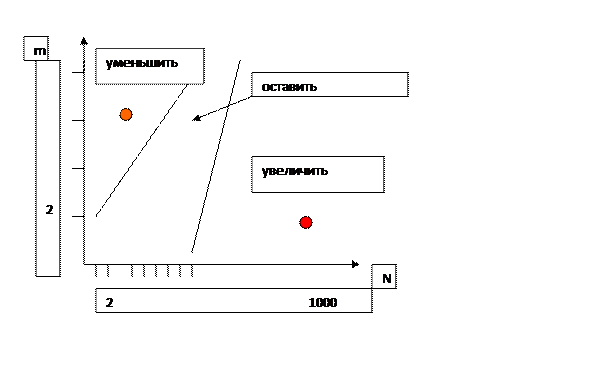
Рис. Номограммы для определения межповерочного интервала

Можно рассчитать:

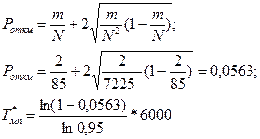- слишком дорого, межпов.интервал можно не пересчитывать

При расчете межповерочного интервала различают следующие режимы работы средств измерений:

1. Установившийся режим – время установления выходного сигнала, время реакции. В этом режиме определяется градуировочная характеристика или функция преобразования.

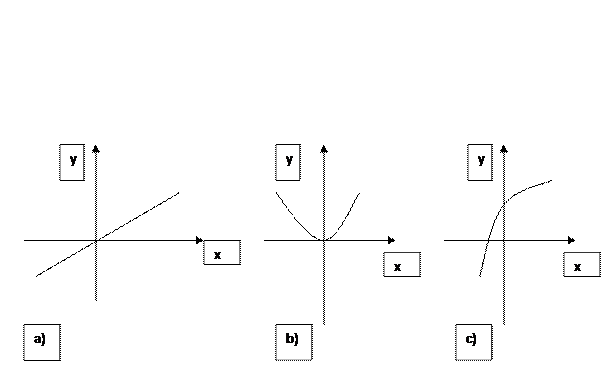
Рис. Функции преобразования средств измерений: а) линейная, может быть представлена коэффициентом преобразования; b) квадратичная; с) логарифмическая

Процедура экспериментального определения функции преобразования отдельного средства измерения в установившемся режиме называется градуировкой .

2. Переходной режим – время воздействия инерционных свойств. В этом режиме Средство измерения не успевает отреагировать на изменение входного сигнала. Отклик средства измерения на единичное входное воздействие – переходная характеристика, описывается уравнениями динамики.

Переходной режим не всегда переходит в установившийся режим.

3. Стационарный режим, при котором параметры выходного процесса непостоянны, но не зависят от времени, постоянны вероятностные характеристики параметров.

4. Нестационарный режим, когда хоты бы один из параметров меняется с течением времени.

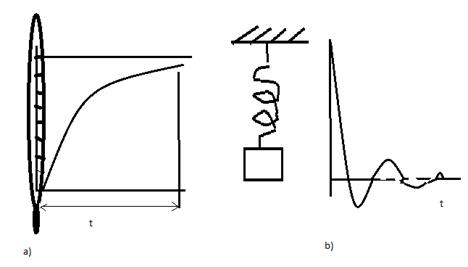
Рис. Установление показаний: а) при измерении температуры; b) при взвешивании груза

Пример: Номинальная функция преобразования – линейная 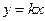. Коэффициент преобразования у отдельных экземпляров 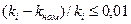(меньше, чем на 1% отклоняется от номинального ). Какой класс точности имеют средства измерения?

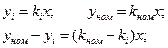
После преобразований ,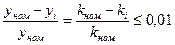

Т.е. относительная погрешность 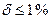, класс точности обозначается .

2.3.6. Регулировка и градуировка СИ

Используя точностные расчеты, всегда можно найти такие допуски на параметры и элементы средств измерений, соблюдение которых гарантировало бы без регулировок обеспечение точностных показателей. Однако эти допуски во многих случаях настолько малы, что изготовление такого средства измерения стало бы либо технологических невозможно, либо экономически нецелесообразно.

Расширяют допуски на отдельные элементы средств измерений за счет использований регулировки и градуировки.

Регулировка СИ – совокупность операций, предназначенных для уменьшения основной погрешности до значений, соответствующих ее допустимым пределам.

В конструкциях СИ предусматривается регулировка нуля и регулировка чувствительности (регулировка погрешностей схемы):

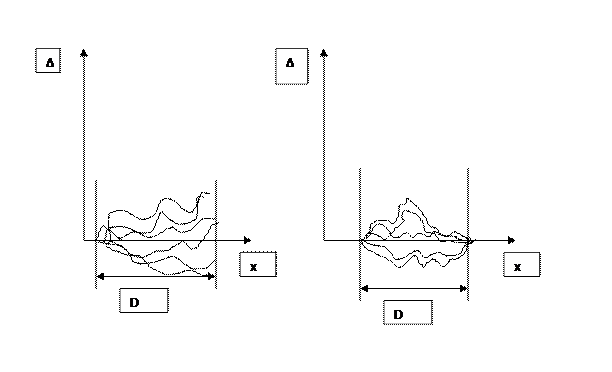
Рис. Уменьшение погрешности СИ за счет регулировки : а) регулировка нуля, b) регулировка нуля и конечного значения

Градуировка – процесс нанесения отметок на шкалы СИ либо определение значений измеряемых величин, соответствующих уже нанесенным отметкам.

Способы градуировки:

1. Использование типовых шкал, в соответствии со статической характеристикой идеального СИ

2. Индивидуальная градуировка шкал (при нелинейных статических характеристик СИ). На предварительно отрегулированное СИ устанавливают шкалу с еще не нанесенными отметками, подают на вход СИ несколько величин с известными значениями, наносят отметки, соответствующие этим значениям.

3. Градуировка условной шкалы: определяют несколько значений шкалы с помощью образцовых СИ, определяют зависимость числа делений шкалы от значения измеряемой величины, шкала – график, таблица.

2.3.7. Методика выбора СИ

При выборе СИ учитывают исходные данные:

1. Номенклатура измеряемых и контролируемых параметров.
2. Допуски на отклонения параметров и суммарная погрешность измерения.
3. Допустимое значение вероятности отказов.
4. Законы распределения вероятностей погрешностей результатов измерения как случайных величин.
5. Номинальные значения, динамический диапазон (мин и макс. значения), частотный диапазон, допустимое время измерения (быстродействие) и т.д.
6. Условия измерения.

При выборе средства измерения по трубуемой точности при