Основные законы математической логики

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

1. Закон двойного отрицания:

не (не А) = A.

Двойное отрицание исключает отрицание.

2. Переместительный (коммутативный) закон:

- для логического сложения:

А v B = B v A;

- для логического умножения:

A & B = B & A.

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

3. Сочетательный (ассоциативный) закон:

- для логического сложения:

(A v B) v C = A v (B v C);

- для логического умножения:

(A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4. Распределительный (дистрибутивный) закон:

- для логического сложения:

(A B) & C = (A & C) (B & C);

- для логического умножения:

(A & B) v C = (A v C) & (B v C).

Определяет правило выноса общего высказывания за скобку.

5. Закон общей инверсии (законы де Моргана):

- для логического сложения:

;

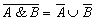- для логического умножения:

.

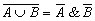6. Закон идемпотентности ( от латинских слов idem - тот же самый и potens -сильный; дословно - равносильный):

- для логического сложения:

A v A = A;

- для логического умножения:

A & A = A.

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

- для логического сложения:

A v 1 = 1, A v 0 = A;

- для логического умножения:

A & 1 = A, A & 0 = 0.

8. Закон противоречия:

A & (не A)= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего:

A v (не A) = 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе - ложно, третьего не дано.

10. Закон поглощения:

- для логического сложения:

A v (A & B) = A;

- для логического умножения:

A & (A v B) = A.

11. Закон исключения (склеивания):

- для логического сложения:

(A & B) v ( & B) = B;

- для логического умножения:

(A v B) & (v B) = B.

12. Закон контрапозиции (правило перевертывания):

(A 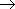B) = (B 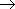A).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

Пример.Упростить логическое выражение: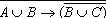

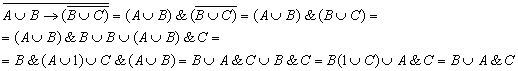
Заключение

Стоит отметить, что на практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики, изучаемых в современных учебниках информатики.

Контрольные вопросы

1. Предмет изучения математической логики.

2. Понятия высказывания, его значений.

3. Содержание операций над высказываниями. Таблицы истинности.

4. Понятие логического выражения (составного высказывания). Примеры.

5. Основные законы математической логики. Примеры.

Литература:

1. Информатика и математика для юристов: учебник для студентов вузов, обучающихся по юридическим специальностям / под редакцией С. Я. Казанцева, Н. М. Дубининой. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2009.

2. Информационные технологии в юридической деятельности: учебник для бакалавров / под общей редакцией П. У. Кузнецова. – М.: Издательство Юрайт, 2012.

3. Симонович С. В. Информатика. Базовый курс. – СПб., Питер, 2011.

[1] Джордж Буль (англ. George Boole; 2 ноября 1815, Линкольн – 8 декабря 1864, Баллинтемпл, графство Корк, Ирландия) — английский математик и логик. Профессор математики Королевского колледжа Корка (ныне Университетский колледж Корк) с 1849. Один из предтеч математической логики.