Логика предикатов первого порядка
Лекции 2-3: Модели и методы решения задач инженерии знаний
Классификация задач представления знаний
Модели представления знаний:
· Логические модели.
· Сетевые модели
· Продукционные модели.
· Сценарии.
Интеллектуальный интерфейс
· Классификация уровней понимания
Методы решения задач инженерии знаний:
· Решение задач методом поиска в пространстве состояний.
· Решение задач методом редукции.
· Решение задач дедуктивного выбора
· Решение задач, использующие немонотонные логики и вероятностные логики.
Классификация задач представления знаний
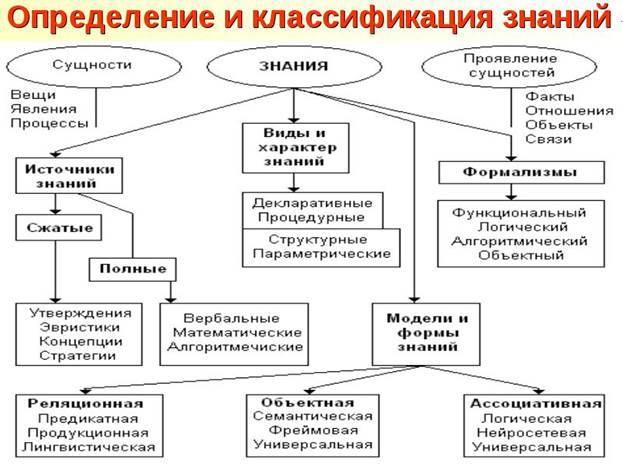
Модели представления знаний
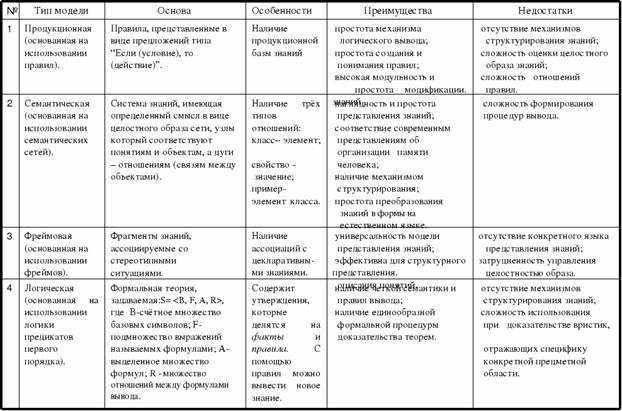
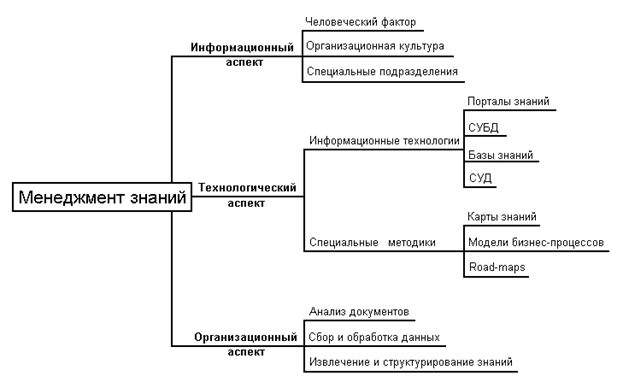
Логические модели
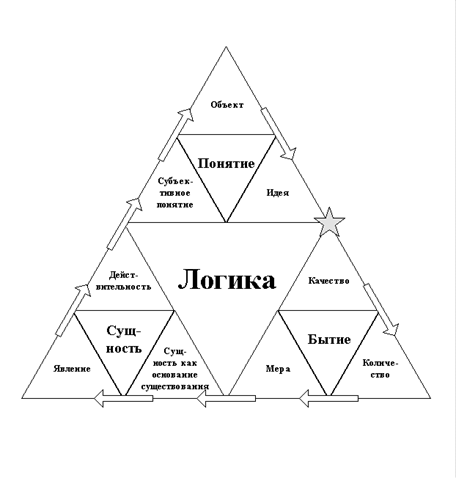
Постановка и решение любой задачи всегда связаны с ее "погружением" в подходящую предметную область. Так, решая задачу составления расписания обработки деталей на металлорежущих станках, мы вовлекаем в предметную область такие объекты, как конкретные станки, детали, интервалы времени, и общие понятия "станок", "деталь", "тип станка" и т. п. Все предметы и события, которые составляют основу общего понимания необходимой для решения задачи информации, называются предметной областью. Мысленно предметная область представляется состоящей из реальных или абстрактных объектов, называемых сущностями.
Сущности предметной области находятся в определенных отношениях друг к другу (ассоциациях), которые также можно рассматривать как сущности и включать в предметную область. Между сущностями наблюдаются различные отношения подобия. Совокупность подобных сущностей составляет класс сущностей, являющийся новой сущностью предметной области.
Отношения между сущностями выражаются с помощью суждений. Суждение-это мысленно возможная ситуация, которая может иметь место для предъявляемых сущностей или не иметь места. В языке (формальном или естественном) суждениям отвечают предложения. Суждения и предложения также можно рассматривать как сущности и включать в предметную область.
Языки, предназначенные для описания предметных областей, называются языками представления знаний. Универсальным языком представления знаний является естественный язык. Однако использование естественного языка в системах машинного представления знаний наталкивается на большие трудности ввиду присущих ему нерегулярностей, двусмысленностей, пресуппозиций и т. п. Но главное препятствие заключается в отсутствии формальной семантики естественного языка, которая имела бы достаточно эффективную операционную поддержку.
Для представления математического знания в математической логике давно пользуются логическими формализмами - главным образом исчислением высказываний и исчислением предикатов, которые имеет ясную формальную семантику и операционную поддержку в том смысле, что для них разработаны механизмы вывода. При этом исчисление предикатов преемственно опирается на исчисление высказываний и по существу есть первым логическим языком, который применили для формального описания предметных областей, связанных с решением прикладных задач.
Описания предметных областей, выполненные в логических языках, называются (формальными) логическими моделями.
Замечание. Логическая модель представляет собой формальную систему — некоторое логическое исчисление, как правило, исчисление предикатов первого порядка. Все знания о предметной области описываются в виде формул этого исчисления или правил вывода. Описание в виде формул дает возможность представить декларативные знания, а правила вывода — процедурные знания. Рассмотрим в качестве примера знание: "Когда температура в печи достигает 120° и прошло менее 30 мин с момента включения печи, давление не может превосходить критическое. Если с момента включения печи прошло более 30 мин, то необходимо открыть вентиль №2". Логическая модель представления этого знания имеет вид:
Р(р = 120) ÙT(t < 30) ® (D <DKp);
Р(р = 120) ÙT(t >30) ®F(№2).
В этой записи использованы следующие обозначения:
Р(р = 120) — предикат, становящийся истинным, когда температура достигает 120°;
T(t < 30) — предикат, остающийся истинным в течение 30 мин с начала процесса;
T(t > 30) — предикат, становящийся истинным по истечении 30 мин с начала процесса;
D < DKp — утверждение о том, что давление ниже критического;
F(№2) — команда открыть вентиль №2.
Кроме того, в этих записях использованы типовые логические связки конъюнкции ( Ù), импликации (®).
Первая строчка в записи представляет декларативные знания, а вторая — процедурные.
Приведём таблицу основных логических операций, на которых основана логика исчисления высказываний.
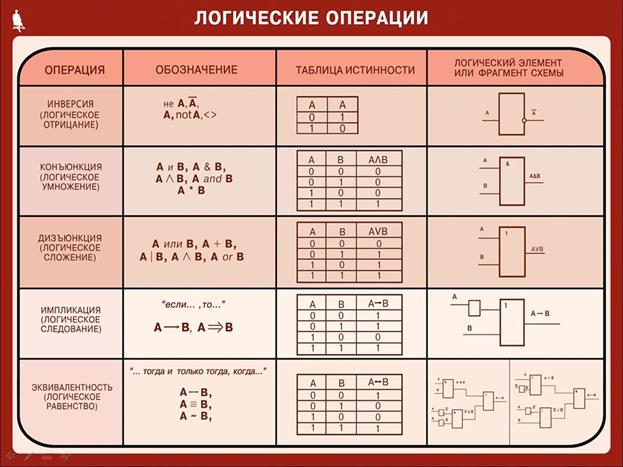
Законы де Моргана:
1) 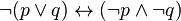 ;
;
2) 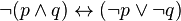 ;
;
Закон контрапозиции:
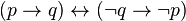 ;
;
Законы поглощения:
1) 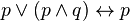 ;
;
2) 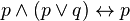 ;
;
Законы дистрибутивности:
1) 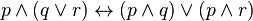 ;
;
2) 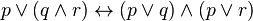 .
.
Исчисление высказываний
Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:
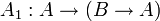 ;
;
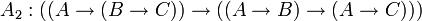 ;
;
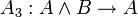 ;
;
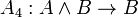 ;
;
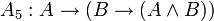 ;
;
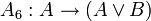 ;
;
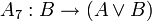 ;
;
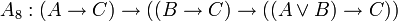 ;
;
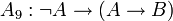 ;
;
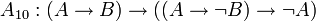 ;
;
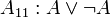 .
.
вместе с единственным правилом:
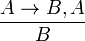 (Modus ponens)*
(Modus ponens)*
*модус поненс
(лат. modus ponens)
термин средневековой логики, обозначающий правило вывода и соответствующий ему логический закон.
Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.
Логика предикатов первого порядка
Недостатком логики высказываний является ее многословность – даже для описания простых задач требуется значительное количество логических переменных и формул. Представление каждого отдельного свойства для каждого конкретного объекта требует отдельной логической переменной, что очень неудобно. Также требуется использовать отдельные переменные для описания всех необходимых комбинаций взаимосвязей между понятиями. С другой стороны, в исчислении высказываний каждый атомарный (элементарный) символ обозначает выражение некоторой произвольной сложности. При этом не существует возможности получить доступ к составным частям этого выражения. Например, фраза «курс доллара имеет тенденцию к росту», обозначенная через логическую переменную 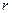 , говорит только о росте курса доллара и не может быть использована в другом контексте (данная фраза является релятивно актуальной (замкнутой) сущностью в рамках прагматики рассмотрения и соответствующих синтаксисо-семантических договореностей.). Логика предикатов позволяет решить эти проблемы представления знаний.
, говорит только о росте курса доллара и не может быть использована в другом контексте (данная фраза является релятивно актуальной (замкнутой) сущностью в рамках прагматики рассмотрения и соответствующих синтаксисо-семантических договореностей.). Логика предикатов позволяет решить эти проблемы представления знаний.
Главная идея логики предикатов заключается во взаимнооднозначном сопоставлении каждого уникального объекта с индивидуальной объектной константой, обозначаемой именем объекта, а класс однотипных объектов – с объектной переменной, значением которой являются объектные константы. Например, выражение, приведенное выше, можно представить на языке логики предикатов так:
изменение_курса (Доллар, Растет).
Очевидно, такое представление гораздо более наглядно и гибко.
Предикатом называют логическую (высказывательную) функцию, определенную на множестве наборов значений объектных переменных. Семантика этой функции определяется предикатным символом, за которым в скобках следуют аргументы (объектные переменные и константы). Эта функция может принимать только два значения: Истина или Ложь, называемые истинностными значениями. Если предикат имеет только один аргумент, то предикатный символ указывает на определенное свойство объекта, а если аргументов несколько – на наличие отношения между объектами, представленными аргументами. Отношения между объектами среды, также как и в логике высказываний, представляются в виде предложений (формул), состоящих из переменных, констант, логических связок, скобок, а также функций, предикатов и кванторов.
Объектная константа или просто константа взаимнооднозначно сопоставляется в процессе интерпретации с каким-либо одним объектом среды и обозначается строкой символов, начинающихся с прописной буквы.
Объектные переменные или просто переменные обозначаются строкой, начинающейся со строчной буквы. Областью значений каждой переменной является множество констант, в общем случае бесконечное.
Объектные константы и переменные являются термами. Как именно выбирать термы для представления знаний – решать разработчику. В приведенном выше примере использовались константы Доллар и Растет. Введем переменную 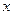 , определенную на множестве валют и переменную динамики изменения курса
, определенную на множестве валют и переменную динамики изменения курса 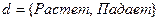 . Предикатный символ изменение_курса ставит во взаимно однозначное соответствие любой валюте свойство плавающего курса. Функция
. Предикатный символ изменение_курса ставит во взаимно однозначное соответствие любой валюте свойство плавающего курса. Функция 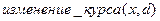 задаёт отношение между объектом валюта и динамикой изменения. Если
задаёт отношение между объектом валюта и динамикой изменения. Если 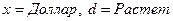 , то в соответствии с теми знаниями что у нас есть («курс доллара имеет тенденцию к росту») изменение_курса (Доллар, Растет) = ИСТИНА.
, то в соответствии с теми знаниями что у нас есть («курс доллара имеет тенденцию к росту») изменение_курса (Доллар, Растет) = ИСТИНА.
С помощью предикатов задаются произвольные отношения между объектами. Предикаты начинаются с предикатного символа и следующими за ним в скобках упорядоченного набора переменных или констант, соответствующих объектам, которые находятся в поименованном отношении. Так, например, если два человека Маша и Саша являются братом и сестрой, то это отношение может быть выражено с помощью предиката
брат_сестра (Маша, Саша).
Предикат может принимать значение Истинно или Ложь. Если предикат Истинен, то отношение имеет место, иначе – наоборот.
Если некоторый объект в точности соответствует множеству других, то используют функции. Например, если объектами являются двоичные цифры и десятичные цифры, то любому двоичному можно однозначно сопоставить десятичное, и выразить это сопоставление в виде функции преобразование_2_в_10(x, y, z), где x, y, z – двоичные числа, а значение функции – десятичное. Выражение преобразование_2_в_10 называют функциональным символом. Функция в логике предикатов не предполагает обязательного наличия алгоритма вычисления ее значения по аргументам. Она лишь задает с помощью констант и переменных определенное отношение между объектами, соответствующими ее аргументам, и каким-то одним объектом. Функции также как и переменные или константы являются термами.
Выражение предикатный_символ (терм, терм, …, терм) называют атомом. Атом представляет предикат. Особо выделяется атом, предикатным символом которого является знак равенства, а аргументами два терма. Этот атом можно было бы представить как равны (терм, терм) или = (терм, терм), но, как правило, его записывают в обычной инфиксной форме терм = терм. Этот атом истинен, когда значения обоих термов совпадают. Атомы без знака отрицания или со знаком отрицания называют литералами.
Когда возникает необходимость выразить какие-либо свойства, общие для целого множества объектов, используют кванторы. В логике предикатов таких кванторов два: 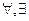 .
.
Квантор общности 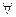 .Смысл квантора общности совпадает с выражением естественного языка «для всех». То есть, если имеется некоторое знание, применимое для любого объекта определённого типа, то вместо перечисления всех таких объектов можно использовать квантор общности.
.Смысл квантора общности совпадает с выражением естественного языка «для всех». То есть, если имеется некоторое знание, применимое для любого объекта определённого типа, то вместо перечисления всех таких объектов можно использовать квантор общности.
Квантор существования 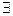 .Если возникает необходимость выразить знание об отдельном объекте из какой-либо совокупности, используют квантор существования. Квантор существования произносится на естественном языке как «существует».
.Если возникает необходимость выразить знание об отдельном объекте из какой-либо совокупности, используют квантор существования. Квантор существования произносится на естественном языке как «существует».
Считают, то квантор связывает переменные, которые записываются за знаком квантора в скобках. Поэтому их называют связанными. Переменные же, которые ни один квантор не связывает, называют свободными.
Взаимосвязь между кванторами существования и общности можно легко выразить с помощью связки отрицания 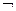 и она основана на следующем соображении: если про любой объект из совокупности можно сказать, что он не обладает заданным свойством, то не существует объекта, обладающего этим свойством. Например, очевидно, что «у любой рыбки нет рук, значит, не существует рыбки, у которой есть руки».
и она основана на следующем соображении: если про любой объект из совокупности можно сказать, что он не обладает заданным свойством, то не существует объекта, обладающего этим свойством. Например, очевидно, что «у любой рыбки нет рук, значит, не существует рыбки, у которой есть руки».
Обозначим любую переменную через 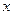 , а любую формулу, содержащую эту переменную через
, а любую формулу, содержащую эту переменную через 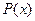 , тогда справедливы следующие законы:
, тогда справедливы следующие законы:
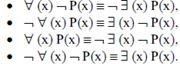
Равенство является атомом особого типа Терм = Терм или = (Терм, Терм). Равенство означает, что оба терма в атоме соответствуют одному и тому же объекту. Не следует путать предикат равенства с операцией присваивания. В следующей таблице раскрыт смысл предиката равенства для различных термов, где X, Y обозначают объектные константы, x, y – объектные переменные, а F(x) – функция:
Таблица -Семантика предиката "равенство"

Синтаксис логики предикатов позволяет наглядно и просто переходить от естественного языка к языку логики предикатов. Достаточно правильно ввести соответствующие объектные константы и предикатные символы, чтобы иметь возможность корректно описывать состояния и явления предметной области. Рассмотрим пример. Предположим, что наши знания о птицах выражены в виде следующих предложений:
· Если существо имеет крылья, то это существо – птица.
· Если существо летает и несет яйца, то это существо – птица.
Алгоритм представления знаний на языке логики предикатов:
1. Выявить, что во фразе является объектом, который необходимо сопоставить с константой или переменной. Если речь идет о конкретном объекте, то вводится константа, если же упоминается целый класс объектов, то используют переменную.
2. Определить свойства объектов. Сопоставить свойствам предикатные символы.
3. С помощью логических связок сформировать формулы констант, переменных и предикатов, соответствующих объектам и их свойствам.
Таким образом, на языке логики предикатов эти знания могут быть выражены в виде формул:
· имеет_крылья(существо) → птица(существо)
· летает(существо) 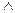 несет_яйца(существо) → птица(существо)
несет_яйца(существо) → птица(существо)
В данном примере использованы одноместные предикаты, имеющие по одному аргументу. В то же время предикаты могут быть также и многоместными, то есть иметь несколько аргументов. В случае многоместных предикатов, как уже было отмечено, предикатный символ может рассматриваться как некоторое общее свойство объектов, соответствующих аргументам, либо как отношение, в котором эти объекты находятся. Вариант первой фразы с применением многоместного предиката может быть, например, следующим:
обладает(существо, крылья) →принадлежит_к_классу (существо, птица).
Нами было рассмотрено исчисление логики высказываний, в частности классическое исчисление. Рассмотрим отличия исчисления предикатов первого порядка от исчисления высказываний.
Аксиомы исчисления высказываний преобразуются в аксиомы исчисления предикатов путем замены 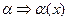 , то есть логическая переменная
, то есть логическая переменная 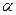 заменяется предикатом
заменяется предикатом 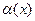 . Кроме того, вводятся две новые аксиомы:
. Кроме того, вводятся две новые аксиомы:
· 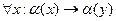
· 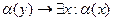
Множество правил вывода включает:
· Обобщенное правило Modus Ponens 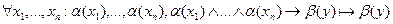 ,
,
и правила введения кванторов
· 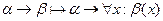
· 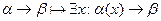 .
.
Существуют также и неклассические исчисления предикатов первого порядка. Они могут строиться на дополнении множества аксиом специфическими для данной предметной области общезначимыми формулами.
Также могут дополнительно использоваться следующие правила вывода:
· Исключение квантора общности: 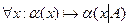 ,
,
· Исключение квантора существования: 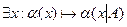 ,
,
· Введение квантора существования: 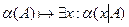 .
.
Здесь 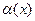 – произвольная формула логики предикатов, имеющая связанную квантором переменную
– произвольная формула логики предикатов, имеющая связанную квантором переменную 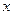 ,
, 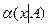 – формула
– формула 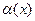 , в которой все вхождения переменной
, в которой все вхождения переменной 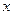 заменены на константу
заменены на константу 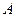 .
.
Следует особо отметить правило исключение квантора общности, которое также называют правилом универсального инстанцирования. Другими словами суть этого правила можно сформулировать так: если любую переменную, стоящую под квантором общности в истинном предложении заменить любым соответствующим термом из области определения, то результирующие выражение истинно.
Однако, в отличие от логики высказываний, логический вывод в пространстве предикатов не так очевиден. Чтобы корректно применять правила вывода типа Modus Ponens, система вывода должна уметь определять, когда два выражения являются эквивалентными, или равносильными. В исчислении высказываний это тривиально:
два выражения равносильны тогда и только тогда, когда они синтаксически идентичны.
В исчислении предикатов определение равносильности двух предложений усложняется наличием переменных. Поскольку все термы в логике предикатов являются символьными, то поиск равносильных предложений сводится к процедуре подстановки 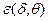 , позволяющей заменить терм δ на другой терм из множества θ.
, позволяющей заменить терм δ на другой терм из множества θ.
Возможны три вида подстановки 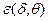 :
:
1. Переименование переменной – вместо переменной δ подставляется переменная из θ.
2. Конкретизация переменной – вместо переменной δ подставляется константа из θ.
3. Замена переменной – вместо переменной δ подставляется функция из θ.
Обязательным условием подстановки является следующее требование. В пределах области действия подстановки, то есть на множестве всех тех предикатов, к которым она применяется, вместо одной и той же переменной δ подставляется одна и та же переменная, константа или функция из θ для всех ее вхождений δ. Процесс поиска нужной подстановки называют также процедурой унификации. Подстановка называется наиболее общей, если в результате ее применения наименьшее число переменных замещается константами. Иногда, в правиле Modus Ponens кванторы общности подразумеваются, но не пишутся, т.е. вместо 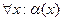 пишут просто
пишут просто 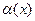 , а кванторы существования вообще не употребляются. Если кванторы существования присутствуют в формуле, то от них следует избавиться, например, с помощью правила исключения квантора существования. Чтобы применять обобщенное правило Modus Ponens, все формулы в постановке задачи должны быть атомами или импликациями, левая часть которых является конъюнкцией атомов, а правая – атомом или пустым символом. Такие формулы получили название хорновскими предложениями. Соответственно, для эффективного вывода в пространстве предикатов, необходимо учитывать приведенные выше ограничения и требования к представлению знаний.
, а кванторы существования вообще не употребляются. Если кванторы существования присутствуют в формуле, то от них следует избавиться, например, с помощью правила исключения квантора существования. Чтобы применять обобщенное правило Modus Ponens, все формулы в постановке задачи должны быть атомами или импликациями, левая часть которых является конъюнкцией атомов, а правая – атомом или пустым символом. Такие формулы получили название хорновскими предложениями. Соответственно, для эффективного вывода в пространстве предикатов, необходимо учитывать приведенные выше ограничения и требования к представлению знаний.
Проиллюстрируем работу правила Modus Ponens в логике предикатов на простом примере. Возьмем известный силлогизм «все люди смертны, и Сократ – человек, поэтому Сократ – смертен». В этой фразе присутствуют три основных высказывания – «все люди смертны», «Сократ – человек» и «Сократ – смертен». Очевидно, необходимо ввести константу «Сократ» и предикатные символы «человек» и «смертен». Тогда фраза «все люди смертны» на языке логики предикатов будет выглядеть так:
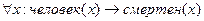 .
.
А фраза «Сократ – человек» так: 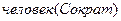 .
.
Поскольку переменная х связана квантором всеобщности, то ее можно заменить любым значением из области ее определения, например Сократ. Следовательно, можно сформировать условие правила Modus Ponens:
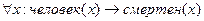
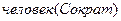
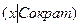 ,
,
а в результате срабатывания этого правила приходим к выводу смертен (Сократ).
Несмотря на потенциальные вычислительные возможности правила Modus Ponens на практике оно используется редко. В основном из-за громоздкости вычислений, необходимых для его применения. Основную часть этих вычислений составляет приведение предложений к импликативному виду, необходимому для формирования условия правила. Более мощным, легко реализуемым и требующем меньше вычислений является правило резолюции. Это правило легло в основу парадигмы логического программирования**, используемого во многих интеллектуальных системах.
