Определение названия и величины румба
Введение
Цель работы: вычислить координаты вершин полигона по исходным данным, построить топографический план, основываясь на теодолитную и тахеометрическую съемку.
Теодолитная съемка- Теодолитной именуется горизонтальная (контурная) съемка местности, в итоге которой может быть получен план с изображением ситуации местности (контуров и местных предметов) без рельефа.
Теодолитный ход- —теодолитным ходом называют построенную на местности (с помощью теодолита) разомкнутую или замкнутую ломаную линию, в которой измерены все стороны и горизонтальные углы между ними, т. е. в основу теодолитного хода положен метод полигонометрии.
Измерения ведутся при рекогносцировочных изысканиях, если отсутствуют карты, позволяющие выбрать направление железно-дорожной линии. Точность таких измерений невелика, но производятся они быстро и дешевоКачество пройденного теодолитного хода определяется путём сопоставления фактических ошибок (неувязок) с допустимыми. Погрешность измерения углов в теодолитном ходе обычно не превышает 1'; а сторон — 1:2000 доли их длины.
Тахеометрическая съемка- вид топографической съемки, при которой горизонтальные и вертикальные углы измеряются по кругам тахеометра, а расстояния до объектов - по его дальномеру. Служит для создания плана участка местности с горизонталями при инженерных изысканиях, геологических, гидрологических и др. исследованиях.
Исходные данные
В исходные данные входит индивидуальное задание с исходными данными величин, измеренных на местности горизонтальных углов, измеренных способом полного приема между вершинами полигона, измеренные расстояния, координаты точек и высотная отметка.
Высота сечения рельефа- 1 метр. (Приложение 1)
| № | Измеренные внутренние углы | Дирекционный угол стороны 1-2 | Горизонтальные положения сторон, м | Координаты | |
| X | Y | ||||
| 63˚43ʹ | 104˚25ʹ | 181,00 | 951,5 | 951,5 | |
| 114˚52ʹ | 108,12 | ||||
| 117˚44ʹ | 104,28 | ||||
| 97˚17ʹ | 120,01 | ||||
| 146˚22ʹ | 134,49 |
Обработка ведомости вычисления координат вершин полигона
Вычисление суммы измеренных углов.
Практическая сумма вычисляется как сумма всех горизонтальных углов, измеренных способом полного приема, и приведенных в исходных данных по формуле:
∑βизм=β1+β2+β3+β4+β5=539°58'
Где β1,β2,β3,β4,β5-горизонтальные углы соответствующих номеров вершин полигона.
Теоретическая сумма углов вычисляется по формуле:
∑βтеор=1800*(n-2)
где n-количество сторон полигона, n=5.
∑βт=1800*(5-2)=5400
Вычисление угловой невязки.
Угловая невязка находится по формуле:
Fβпр=∑βизм-∑βтеор
Ʃβизм = β1 + β2 + β3 + β4 + β5 = 63˚43ʹ + 114˚52ʹ + 117˚44ʹ + 97˚17ʹ + 146˚22ʹ = 539˚58ʹ
Подставим значения теоретической и практической суммы измеренных углов, получаем угловую невязку:
Fβпр=539058′-5400=-0002′
Расчет допустимой невязки находится по формуле:
Fβдоп=±х√2
Fβдоп=±1х*√5≈±2,2
Сравним теоретическую и полученную невязки:
Fβизм < Fβдоп
Вычисление дирекционных углов.
Дирекционный угол линии- это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°. Зная дирекционный угол одного хода, вычисляют дирекционные углы всех остальных ходов для полигона.
Зависимость между дирекционными углами и углами поворота в теодолитном ходе вычисляют по формуле:
αпосл.=αпред+180°-βправая, для правых углов
αпосл= αпред-180°+βлевая, для левых углов
Так по данным у нас углы правые, тогда:
α2-3=α1-2+180°-β2,
α3-4= α2-3+180-β3, и т.д.
Дирекционный угол исходного направления=104о25′
α1-2= 104о25′
α2-3 = α1-2 +180о – β2=104о25′+180о - 114о52′=169о33′
α3-4 = α2-3 +180о – β3=169о33′+180о - 117о45′=231о48′
α4-5 = α3-4 +180о – β4=231о48′+180о - 97о18′=314о30′
α5-1 = α4-5 +180о – β5=314о30′+180о - 146о22′=348о08′
Контроль вычисления дирекционных углов:
В конце вычисления должны получить точное значение дирекционного угла конечной стороны хода:
α1-2= α5-1 +180о – β1=348о08′+180о - 63о43′=528о08′- 63о43′- 360о=104о25′
Следовательно, можно считать, что дирекционные углы рассчитаны верно.
Определение названия и величины румба.
Румб-горизонтальный острый угол отсчитываемый от ближайшего северного или южного направления меридиана до ориентируемого направления. Румбы имеют названия в соответствии с названием четверти, в которой находится линия, т.е.: северо-восточные СВ, северо-западные СЗ, юго-западные ЮЗ, юго-восточные ЮВ. На рис. показаны румбы линий О-СВ, О-ЮВ, О-ЮЗ, О-СЗ и зависимость между дирекционными углами и румбами этих линий.
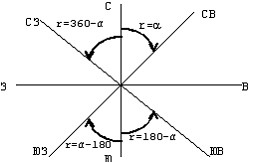
II четверть 1.ЮВ r1 =180- α1 = 180о-104о25′=75о35′
II четверть 2.ЮВ r2 = 180о – α2= 180о – 169о33′ = 10о27′
III четверть 3.ЮЗ r3 = α3-180о= 231о48′-180о = 51о48′
IV четверть 4.СЗ r4 = 360 - α4 =360о - 314о 30′= 45о30′
IV четверть 5.СЗ r5 = 360о – α5= 360о - 348о08′ = 11о52′
