Основные методы преобразования изображений для повышения их контрастности

Значительная часть задач обработки информации и анализа данных связана с изображениями. Примерами могут служить обработка и анализ данных дистанционного зондирования Земли со спутников, объемные изображения объектов, полученные с помощью голографических устройств, результаты применения методов неразрушающих исследований и контроля в промышленности, разработка “органов зрения” роботов и современных медицинских систем диагностики (рентгенография, машинная томография, эндоскопия и т.д.). Для успешного решения задач поиска и идентификации объектов, определения различного рода их количественных характеристик необходимо, чтобы первичные изображения характеризовались высоким визуальным качеством, которое теряется из-за неудовлетворительных условий получения изображений, несовершенства систем передачи видеоинформации и ее отображения, влияния помех и т.п.

Поэтому актуальной является задача преобразования изображений с целью улучшения их визуального качества и повышения информативности. Все основное множество методов, которые решают эту задачу, делится на методы обработки в частотной и пространственной областях. Для обработки изображений в пространственной области наибольшее распространение получили методы пяти классов:

1) методы растяжения;
2) гистограммные методы;
3) ранговые методы;
4) разностные методы;
5) методы преобразования локальных контрастов.

К преимуществам методов обработки изображений в пространственной области относится возможность быстрой обработки в масштабе реального времени телевизионного видеосигнала, а к недостаткам - ограниченность функциональных возможностей и недостаточная эффективность.

При рассмотрении методов обработки изображений всегда остро стоит вопрос выбора критериев оценки качества их преобразования. Этот вопрос всегда был актуальным, однако ставился и решался он разными способами. В дальнейшем материале рассмотрим известные современные подходы к решению этой задачи [12].

Разделение на классы условно, поскольку все методы имеют в своей основе локальный контраст элементов изображения.

Хотя способы обработки изображений в частотной области и достаточно развиты, но требуют значительных вычислительных затрат и для решения практических задач применяются реже. Поэтому в дальнейшем рассмотрим основные методы обработки изображений в пространственной области, а именно методы растяжения, гистограммные, ранговые, разностные и методы преобразования локальных контрастов.

Список литературы

1. Абакумов В.Г., Крылов В.Н., Антощук С.Г. Обнаружение и распознавание признаков объектов с помощью сферической модели зрительного анализатора // Электроника и связь. – 2000. – №8. – т. 2.–С. 211 – 212.

2. Эргономика зрительной деятельности человека / В.В. Волков, А.В. Луизов, Б.В. Овчинников, Н.П. Травникова. – Л.: Машиностроение. Ленингр. Отд–ние, 1989. – 112 с.

3. Bouguer P. Traite d’Optique surla Gradation de la Lumiere. I’Abbe de Lacaille. – Paris, 1760.

4. Fechner G.T. Elemente der Psychophysik. – Leipzig. – 1860.

5. Fechner G.T. Vebereinige Verhaltnisse des binocularen Sehens // Abhandl. Sachsische Gesellschaft d. Wissensch. – 1870. –№ 7.

6. Шашлов Б.А. Теория фотографических процессов. –М.: Книга, 1981. – 319 с.

7. Нестерук В.Ф., Порфирьева Н.Н. Контрастный закон восприятия света // Оптика и спектроскопия. – 1970. – Т. ХХІХ, вып. 6. – С. 1138 – 1143.

8. Nesteruk V.F., Porfirieva N.N. Vision Research. – 1974. – v. 14, № 9. – p. 899 – 904.

9. Гранрат Д.Дж. Роль моделей зрения человека в обработке изображений // ТИИЭР. – Т. 69. – № 5. – 1981. – С. 65 – 77.

10. Мирошников М.М.Теоретические основы оптико–электронных приборов. – Л.: Машиностроение, 1983. – 696 с.

11. Нестерук В.Ф., Порфирьева Н.Н. Информационная оценка процесса зрительного восприятия // Оптика и спектроскопия. – 1978. – Т. 44, вып. 4. – С. 801 – 803.

12. Журавель И.М. Локально-адаптивные методы повышения контрастности изображений: Дис… канд. техн. наук: 05.13.06. – Львов, 2001. – 154 с.

Оценка визуального качества цифровых изображений

Рассмотрим наиболее известные методы оценки качества изображений.

Качество изображения определяется большим количеством технических характеристик системы: соотношением сигнал/шум и статистическими характеристиками шума, градационными характеристиками, спектральными (цветовыми) характеристиками, интервалами дискретизации и т.д.

Одним из параметров, которые определяют качество изображений, является контраст. Поскольку изображение имеет сложный сюжетный характер, то это порождает необходимость при определении его контрастности выходить из контраста отдельных комбинаций элементов изображения. При этом все элементы считаются равнозначными, и контраст каждой их пары вычисляется по формуле

, (1)

где , - яркости элементов сюжетного изображения.

Сюжетность изображения предполагает возможность его использования человеком. Поэтому при оценке контраста, как одного из параметров качества изображения, необходимо учитывать ряд особенностей зрительного восприятия человека.

Далее, применяя правило суммирования контрастов, вычисляют набор величин, которые определяют восприятие каждой пары элементов изображения. Проводя усреднение матрицы локальных контрастов, получают суммарный контраст. Полученный результат может быть использован как один из параметров оценки визуального качества изображения [1].

Существует еще один метод оценки качества изображения. Его суть состоит в следующем. Экспериментально было установлено, что оптимальное, с точки зрения субъективного восприятия, изображение имеет нормальное распределение яркостей его элементов. Для удобства дальнейших расчетов был применен критерий нормального распределения. По степени отклонения реального распределения яркостей от нормального проводилась оценка качества изображения. Кроме количественной оценки качества изображения, данный метод позволяет получить информацию о наличии и весовом соотношении яркостных градаций изображения. Результаты оценки качества изображения, полученные по данному методу, хорошо коррелируют с субъективной оценкой визуального качества изображения [2].

Рассмотрим еще один известный эмпирический подход к оценке визуального качества изображения [5]. Для формирования этой оценки рассматриваются такие параметры изображения как среднеарифметическое значение яркостей, полнота использования градаций яркостей, резкость изображения и его обобщенный контраст.

Величина отображает уровень адаптации по яркости зрительной системы человека, оптимальным значением которой является половина максимально возможного диапазона яркостей . Поэтому величину отклонения от можно использовать как оценку уровня адаптации зрительной системы:

. (2)

Вторым важным параметром оценки визуального качества изображения является полнота использования его элементами градаций яркостей. Аналитическое выражение этого параметра такое:

, (3)

где - количество уровней яркостей, для каждого из которых на данном изображении присутствуют большее чем количество элементов с данной яркостью ( и - размеры изображения, - некоторая константа).

Третьим параметром оценки визуального качества изображения в данном методе является его резкость, которая измеряется скоростью нарастания яркости, разделенной на общую величину перепада [3]:

, (4)

где - это видеосигнал; и - точки, которые расположены на противоположных краях перепада. Поэтому оценку резкости находят следующим образом

. (5)

Четвертый параметр дает оценку контраста изображения. Когда оценивается визуальное качество изображения независимо от его сюжетного наполнения, тогда за принимают обобщенный контраст изображения [5].

В целом выражение для количественной оценки визуального качества полутоновых монохромных изображений записывают так [5]:

, (6)

где - нормирующий коэффициент.

Существуют также иные комплексные критерии качества изображений. Их суть состоит в следующем. Подразумевается, что человек-оператор может сам оценить важность отдельных параметров качества изображения ,... , для различных классов искажений. После этого строится некоторая комплексная оценка . Примером могут быть комплексные оценки вида [4]:

, (7)

. (8)

Весовые коэффициенты или учитывают относительную важность частичных оценок в комплексной оценке качества.

Рассмотрим еще один метод определения комплексной оценки качества изображения [5]. Его особенность состоит в том, что все частичные оценки комплексного критерия качества будут рассматриваться с точки зрения единой вероятностной модели изображения и определяться на основе моментов гистограммы.

Экспериментальные исследования данного метода дают результаты, которые хорошо согласуются с субъективной визуальной оценкой.

Предложенный метод целесообразно применять для оценки визуального качества незашумленных изображений. Большинство известных подходов использует лишь один параметр качества изображения. Преимущество этого метода состоит в том, что в нем используется интегральный критерий вычисления визуального качества. Он объединяет самые важные показатели качества, определение которых исходит из единой вероятностной модели изображения. Чем большее количество параметров качества изображения будет учтено, тем точнее будет оценка. Тем не менее, для этого метода следует иметь в виду, что при увеличении количества параметров, возрастает его вычислительная сложность.

Пусть одно и то же изображение улучшается двумя различными методами. В результате обработки получим два изображения. Применив к ним предложенный метод, получим две количественные оценки качества. Поскольку эти изображения были получены из одного и того же исходного изображения, то, анализируя эти оценки, можно сравнивать эффективность методов их обработки. Таким образом, предложенный метод является инструментом оценки качества преобразованных изображений и эффективности методов, которые реализуют эти преобразования.

Для тестирования метода поступаем так. Одно и то же изображение обрабатываем методом усиления локальных контрастов и методом низкочастотной фильтрации. Полученная серия изображений - ухудшенное, входное и улучшенное - имеет соответственно самые низкие, средние и самые высокие количественные оценки качества. Приведем результаты экспериментальных исследований и соответствующие им количественные оценки качества для трех различных по своей природе изображений.

1- ,	2- ,	3- ,
4- ,	5- ,	6- ,
7- ,	8- ,	9- ,

Рис. 1. Иллюстрация применения метода количественной оценки качества изображений.

Из рисунка 1 видно, что для серий изображений минимальную оценку качества имеют изображения, которые были размыты (первая колонка), а максимальную - обработанные методом улучшения (третья колонка). Полученная количественная оценка хорошо коррелирует с визуальным восприятием. Проведенные исследования известных методов оценки качества изображений показали, что они являются менее эффективные по сравнению с предложенным методом. Недостатком же предложенного метода является некорректная оценка качества зашумленных изображений. Этот недостаток присущ всем методам, которые при оценке качества изображения используют ту или иную меру контраста. Это связано с тем, что метод оценки качества не обеспечивает идентификации резких перепадов яркостей - по шуму или высококонтрастному участку.

Кроме уже упомянутых в работе, к наиболее употребляемым объективным оценкам качества изображения относятся [8]:

средняя разность -

; (9)

нормированная корреляция (normalized cross-correlation) -

; (10)

качество корреляции (correlation quality) -

; (11)

максимальная разность (maximum difference) -

; (12)

верность изображения (image fidelity) -

; (13)

среднеквадратичная лапласианова погрешность (laplasian mean square error) -

(14)

где ;

среднеквадратичная погрешность (mean square error) -

; (15)

максимальная среднеквадратичная погрешность (peak mean square error) -

; (16)

нормированная абсолютная погрешность (normalized absolute error) -

; (17)

нормированная среднеквадратичная погрешность -

; (18)

норма (Минковского) -

, ; (19)

отношение сигнал/шум -

; (20)

максимум отношения сигнал/шум -

. (21)

Оценки качества, представленные выражениями (9) - (21) удобные в пользовании, тем не менее, они не всегда позволяют объективно оценить качество изображения, в особенности с точки зрения его визуального восприятия.

Вопрос количественной оценки качества изображений до конца не решен. Он является важным шагом на пути к решению задач оптимальных преобразований изображений с точки зрения визуального восприятия.

Список литературы

1. Гуров А.А., Порфирьева Н.Н. Вопросы оценки контрастности сюжетных изображений // Труды ГОИ им. С.И.Вавилова. – т. 44, вып. 178. – Л. – 1979. – C. 31 – 34.
2. Смирнов А.Я. Критерии качества дискретизированных изображений // Труды ГОИ им. С.И.Вавилова. – т. 57. – вып. 191. – Л. – 1984.
3. Розенфельд А.Распознавание и обработка изображений. – М.: Мир, 1972. – 230 с.
4. Мирошников М.М., Нестерук В.Ф. Дальнейшее развитие методологических основ иконики // Труды ГОИ им. С.И.Вавилова. – т.64, вып. 198. – Л. – 1987. – C. 5 – 11.
5. Воробель Р.А., Журавель І.М., Опыр Н.В., Попов Б.О., Дереча В.Я., Равлик Я.М. Метод количественной оценки качества рентгенографических изображений // Труды Третьей Украинской научно–технической конференции “Неразрушающий контроль и техническая диагностика – 2000”. – Днепропетровск. – С. 233 – 236.
6. Шлихт Г.Ю. Цифровая обработка цветных изображений. – М., Издательство ЭКОМ, 1997. – 336 с.

Приложение. Программа, реализующая оценивания визуального качества изображений по одному из изложенных выше методов (формулы (2)-(6))

clear;
% Здесь производится считывание изображения в формате img, для стандартных форматов используют функцию imread.
fid=fopen('D:\len.img','r');
[A,count]=fread(fid,'char');
fclose(fid);
M=input('Высота изображения M=');
N=input('Ширина изображения N=');
K=255; A=A(9:length(A));
LQ=1-(abs(sum(A)/(M*N)-K/2))/(K/2); % оценка уровня адаптации зрительной системы
A=A+1; Amin=min(min(A)); Amax=max(max(A));
H=hist(A,Amax-Amin+1);
S=0;
for i=Amin:Amax;
if H(i-Amin+1)>.001*M*N;
S=S+1;
else S=S;
end;
end;
KQ=S/K; % оценка степени использования возможных градаций яркостей
A=A-1;
m=15;n=15;n1=fix(n/2);m1=fix(m/2);
L=reshape(A,N,M); % преобразование матрицы изображения с целью устранения краевого эффекта
a=L(1,1); b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a;L3(i,j)=b;L6(i,j)=c;L8(i,j)=d;
end;
end;
L2=L(1,1:M);
L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M);
L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1);
L4=L4';
L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4';
L5=L(1:N,M);
L5=L5';
L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5';
L1=[L1;L4];
L1=[L1;L6];
L1=L1';
L2=[L2;L];
L2=[L2;L7];
L2=L2';
L3=[L3;L5];
L3=[L3;L8];
L3=L3';
L1=[L1;L2];
L1=[L1;L3];
L1=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;clear L7;clear L8;clear L02;clear L04;clear L05;clear L07;
F=ones(n,m);
Lser=filter2(F,L1,'same')/(n*m);
L0=Lser(n1+1:N+n1,m1+1:M+m1);LA=L1(n1+1:N+n1,m1+1:M+m1);
LB=L1(n1+1:N+n1,m1+2:M+m1+1);LC=L1(n1+2:N+n1+1,m1+1:M+m1);
Delta=abs(LA-LB)+abs(LA-LC);
RQ=sum(sum(Delta.^2))/((M*N)*(K/2));% резкость изображения
L=L1(n1+1:N+n1,m1+1:M+m1);
Lgl=sum(sum(L))/(M*N);Lmin=min(min(L));Lmax=max(max(L));
LH=L+1;LH=LH(:);
H=hist(LH,Lmax-Lmin+1);
H=H./(M*N);
for l=Lmin:Lmax;
disp(l);
C(l+1)=(1/510)*abs(2*(l-Lgl)+255-abs(2*(l-Lgl)-255))*H(l-Lmin+1);
end;
KC=sum(sum(C));% контрастность изображения
Q=100*KC*LQ*KQ*RQ;
disp('Интегральный критерий');
disp(Q);

Обзор методов цифровой обработки изображений

Обработка изображений является многоплановой задачей. Сюда включают решение задач фильтрации шумов, геометрической коррекции, градационной коррекции, усиления локальных контрастов, резкости, восстановления изображений и др.

Методы обработки изображений разделяют на два класса. Первый - методы обработки в частотной области, второй - методы обработки в пространственной области.

Методы обработки изображений в частотной области базируются на соответствующих моделях зрения человека, например, модели Стокхема [1], Ч.Холла и Э.Холла [2]. Эти модели показывают, что эффективное изменение визуального качества изображения можно проводить через изменение двух основных составных частей изображения - низкочастотной (фоновой) и высокочастотной (детальной). Алгоритмы обработки в частотной области имеют большую вычислительную сложность, которая ограничивает их использование для обработки изображений в масштабе реального времени. Однако, линейная фильтрация широко используется в когерентных оптических системах обработки информации, где как и в цифровой обработке, сигналов она базируется на использовании быстрых алгоритмов свертки и спектрального анализа [3]. Параметры необходимых фильтров преимущественно определяют, пользуясь принципами оптимальной (винеровской) фильтрации [4], разработанной для среднеквадратического критерия качества фильтрации [5]. Достижения теории фильтрации широко используют при обработке изображений [6]. Так, согласующая фильтрация применяется в обработке изображений с позиций не просто повышения качества, а для выявления объектов на изображениях. Реальные системы формирования изображений не являются идеальными из-за аберрации, смазывания изображения во время экспозиции, низкого контраста, наличия атмосферных неоднородностей и т.п. Поэтому для этих систем в предположении их линейности и стационарности можно значительно улучшить качество изображений, применяя технику инверсной фильтрации [7].

Метод инверсной фильтрации никак не учитывает шумовых эффектов, поэтому не удивительно, что он дает плохие результаты при наличии шума. Методы винеровской фильтрации учитывают априорное значение статистических свойств шума и потому позволяют повысить качество возобновляемых изображений. При использовании метода пространственной реставрации изображений на основе регрессии шумовое поле моделируют некоторой реализацией двумерного случайного процесса с неизвестными средним и ковариационной функцией. Тогда применяют винеровское оценивание в предположении, что идеальное изображение также является реализацией двумерного случайного процесса с известными первым и вторым моментами [8]. Представляя результирующее изображение как свертку входного изображения с импульсной передаточной характеристикой или функцией размывания точки оптической системы, которая вносит искажение, для восстановления изображения используют также итерационный алгоритм Бугера-Ван-Циттера [9].

Обобщая сжатый обзор некоторых алгебраических методов восстановления изображений, отметим, что он является составной частью более широкой проблемы решения некорректных задач восстановления изображений [10], включая реконструкцию изображений по проекциям (реконструктивную томографию) [11]. Рядом с этими методами широко используются методы линейной фильтрации для улучшения изображений.

Основой большинства методов линейной фильтрации в пространственной области являются ортогональные преобразования. Существует три основных области применения двумерных ортогональных преобразований для обработки изображений [12]. Во-первых, преобразования используют для выделения характеристик признаков изображения. Второй областью применения является кодирование изображений, когда ширина спектра уменьшается за счет отбрасывания или грубого квантования малых по величине коэффициентов преобразования. Третья область применения - это сокращения размерности при выполнении вычислений. К таким преобразованиям принадлежат преобразования Фурье, синусные, косинусные, волновые преобразования, а также преобразования Карунена-Лоева, Уолша, Хаара и Адамара. Однако и эти преобразования не обеспечивают обработки изображений в масштабе реального времени из-за своей вычислительной сложности.

Другой подход к обработке изображений с целью улучшения их визуального качества состоит в непосредственном использовании разных фильтров. Область их функционирования - в основном частотная и реже - пространственная. Для этого используют разные методы синтеза фильтров, как одномерных, так и двумерных, чем обеспечивают реализацию заданных частотных характеристик.

Проведенный анализ показывает, что использование фильтрации изображений с целью повышения их визуального качества с обеспечением высокого быстродействия является наиболее рациональным при реализации в пространственной области. Однако арсенал алгоритмических средств обработки при этом является недостаточным. Использование же обработки в частотной области хотя и достаточно развито, но требует значительных вычислительных затрат.

• Ранговые методы

Список литературы

1. Стокхэм мл. Обработка изображений в контексте модели зрения // ТИИЭР. - 1972. - T.60, N 7. - С.93-108.
2. Hall Ch.F., Hall E.L. A nonlinear model for the spatial characte-ristics of the human visual systems. - IEEE Trans. Syst. Man and Cybern. - 1977. - V.SMC-7, - P. 161-170.
3. Власенко В.А., Лаппа Ю.М., Ярославский Л.П. Методы синтеза быстрых алгоритмов свертки и спектрального анализа. - М.: Наука, 1990. - 180 с.
4. Боде Г., Шеннон К. Упрощенное изложение линейной минимально-квадратичной теории сглаживания и предсказания // Теория информации и ее применение. - М.: Физматиз, 1959. - С.113-137.
5. Виткус Р.Ю., Ярославский Л.П. Адаптивные линейные фильтры для обработки изображений // Адаптивные методы обработки изображений / Под ред. В.И.Сифорова и Л.П.Ярославского.- М.: Наука, 1988. - С.6-35.
6. Andrews H. C.Monochrome digital image enhancement. Applied Optics, 1976. - Vol.15, N 2. - P. 495-503.
7. Стокхэм Т. мл., Кэннон Т.М., Ингебретсен Б.Б.Цифровое восстановление сигналов посредством неопределенной инверсной свертки // ТИИЭР.-1975.-T.63, N 4. - С. 160-177.
8. Pratt W.K.Generalized Wiener Filter Computation Techniques. IEEE Trans. Computers. - 1972. - V.C-21, N 7. - P. 636-641.
9. Бьемон Ж., Лагендейк Р.Л., Марсеро Р.М. Итерационные методы улучшения изображений // ТИИЭР. - 1990. - T.78, № 5. - С. 58-84.
10. Бертеро М., Поджо Т.А., Торре В. Некорректные задачи в предварительной обработке визуальной информации // ТИИЭР. - 1988. - T.76, № 8. - С. 17-40.
11. Бейтс Р., Мак-Донелл М. Восстановление и реконструкция изображений. - М.: Мир, 1989. - 333 с.
12. Pratt W.K.Digital Image Processing.- New York: J. Wiley, 1978. - 750 p.

Обзор методов цифровой обработки изображений: Ранговые методы

Существующие методы цифровой обработки изображений с позиций использования вычислительных средств можно разделить на две категории - структурированные и неструктурированные методы.

Структурированные методы – такие, которые построены на использовании крупных вычислительных (программных) блоков, оперирующих векторами отсчетов, а не отдельными отсчетами изображений. Cреда MATLAB позволяет реализовывать методы обработки изображений, оперирующие не только с векторами, но и с массивами отсчетов.

Неструктурированные методы – те, которые нельзя представить более крупными стандартными блоками, чем обычные для существующих цифровых вычислительных машин арифметико-логические операции над отдельными отсчетами сигналов. Неструктурированные методы, как правило, возникают на начальной стадии поиска решения содержательных задач обработки изображений и по мере нахождения решения перерастают в структурированные.

Структурирование методов обработки изображений – основа повышения их вычислительной эффективности, построения вычислительных машин обработки изображений и специального математического обеспечения таких машин.

Рассмотрим класс структурированных нелинейных алгоритмов, которые осуществляют преобразование вида

,

где – нелинейная функция, которая определяется некоторым подмножеством рангов и (или) порядковых статистик выборки, образованной отсчетами сигнала из некоторой окрестности данного элемента, в последовательности упорядоченных отсчетов сигнала. Поэтому класс алгоритмов называется ранговыми алгоритмами [1, 2, 3].

Обозначим через 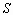окрестность элемента изображения, (k,l) - заданное определенным образом множество, окружающее центральный элемент. М-окрестность - подмножество элементов 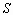-окрестности. Варианты M-окрестностей могут быть самыми разнообразными. Приведем некоторые примеры:

• KSN - окрестность из К элементов, ближайших на растре к данному элементу;
• KNV - окрестность из К ближайших соседей к данному элементу по значению сигнала:
  .

• EV – окрестность:
  .

Медиана элементов М-окрестности:

.

Приведенные статистики удобно искать по локальной гистограмме. Существующие рекурсивные алгоритмы позволяют быстро обрабатывать окрестности любых размеров.

Преимуществом ранговых алгоритмов является их отличие от методов линейной фильтрации, они лишены такого характерного недостатка как пространственная инерционность, которая заключается в том, что при использовании линейных фильтров влияние отдельных деталей изображения проявляется на результирующем изображении на расстоянии порядка размеров апертуры фильтра. Это заметно в частности в размывании границ деталей при сглаживании изображений, в искажении формы деталей при их выделении из фона и т.п.

На первый взгляд может показаться, что вследствие переупорядочивания данных в вариационный ряд ранговые алгоритмы не используют пространственных связей между элементами изображений, и это является принципиальным недостатком. Действительно, ранговые алгоритмы инвариантны к пространственным связям и даже к размерности сигнала. Однако, как ни удивительно, это свойство является не недостатком, а преимуществом ранговых алгоритмов, еще одной стороной их адаптивного характера.

Пространственные связи между элементами изображения, определяемые, например, принадлежностью их к одной детали, проявляют себя в вариационном ряду через параметры условной гистограммы распределения значений сигнала в окрестности данного элемента.

В последнее время появилось много публикаций, в которых рассматриваются алгоритмы, основанные на вычислении линейной комбинации порядковых статистик, взятых с заранее подобранными из тех или иных соображений весами. Ранговые алгоритмы могут использоваться во всех процедурах обработки изображений – стандартизации, сглаживания, усиления детальности, выделения объектов из фоновой части, выделения границ, определения статистических характеристик и т.д. [6].

Ранговые алгоритмы локально-адаптивны по своей сути, поскольку их параметры являются функциями локальной характеристики изображений - локальной гистограммы.

Термин "ранговые алгоритмы" в обработке изображений появился относительно недавно, когда множество алгоритмов, которые фактически относятся к классу ранговых, были уже достаточно известны. Еще в работе [4] было введено понятие адаптивных амплитудных преобразований. Для фильтрации импульсных помех и сглаживания изображений давно используется предложенный Тьюки [5] алгоритм медианной фильтрации. Известны также алгоритмы экстремальной фильтрации, которые используют значения минимума и максимума в окрестности. Все эти алгоритмы можно рассматривать как частные случаи широкого класса ранговых алгоритмов.

Методы ранговых преобразований позволяют осуществить нелинейное усиление высокочастотной составляющей изображения. Это приводит к повышению детальности изображений, однако сопровождается уменьшением контрастности тонкоструктурных объектов [1, 7]. Возможным вариантом устранения этого недостатка является использование взвешенных ранговых преобразований [2, 3].

Кроме применений для сглаживания, усиления детальности, выделения деталей изображений и границ деталей, ранговые алгоритмы можно употреблять для решения многих других задач обработки изображений, в частности, для диагностики статистических характеристик искажений видеосигнала, стандартизации изображений, определения статистических характеристик видеосигнала и измерения текстурных признаков.

Применимость ранговых алгоритмов для кодирования связана с возможностями адаптивного квантирования мод при пофрагментной (не скользящей) обработке.

В пакете IPT предложены некоторые функции ранговой обработки изображений. Функция D=ordfilt2(S, order, domain) позволяет пикселю изображения D, соответствующему центральному элементу маски, присвоить значение с номером order в отсортированном (по возрастанию) множестве. Функция D=ordfilt2(S, order, domain, А) работает аналогично функции D=ordfilt2(S, order, domain), за исключением того, что перед сортировкой к значениям пикселей, соответствующих ненулевым элементам маски фильтра domain, прибавляются значения из матрицы А. Частным случаем ранговой фильтрации является медианная фильтрация.

Анализ и сравнение приведенных выше теоретических основ ранговых методов и функций пакета обработки изображений в системе MATLAB приводит к выводу о необходимости создания программных средств, реализующих методы ранговой обработки изображений. Такие работы проводятся. Они позволяют не только исследовать существующие алгоритмы, но и, выявив их недостатки, создавать новые высокоэффективные методы ранговой обработки изображений. Приведем пример программы ранговой обработки изображений.