Исключение промахов (грубых погрешностей)

Промах, или грубая погрешность, – это погрешность результата единичного (отдельного) измерения, входящего в ряд измерений, которая для данных условий измерений резко отличается от остальных результатов этого ряда.

Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Их причиной возникновения могут быть:

1. объективная реальность (наш реальный мир отличается от нашей идеальной модели мира, которую мы принимаем в данной измерительной задаче);

2. внезапные кратковременные изменения условий измерения (вызванные неисправностью аппаратуры или источников питания);

3. ошибка оператора (неправильное снятие показаний, неправильная запись и т.п.).

В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.

Однако если резкое отличие результата вызвано первой причиной, то тем самым «отбрасывается открытие». Надо сказать следующее: - эксперимент всегда таит неожиданности. Если такое случается, а это редко, но все таки бывает, то следует тщательно зафиксировать все (не только «протокольные») условия измерения, время измерения, все физико-химические параметры сред и т. п., а затем попытаться вновь повторить эксперимент с более точной аппаратурой. Как правило, открытие нового эффекта или «аномалии» при этом бывает в смежной области.

Сложности возникают при обработке готового материала эксперимента – результата наблюдения (ранее это было официальным термином). В этом случае прибегают к методам математической статистики – к общим методам проверки статистических гипотез [35, 42].

Задаются вероятностью p или уровнем значимости q (q = 1 – p) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».

Критерий «трех сигм»применяется для случая, когда измеряемая величина x распределена по нормальному закону. Как выше указывалось, по этому критерию считается, что с вероятностью p = 0,9973 и значимостью q=0,0027 появление даже одной случайной погрешности, большей, чем 3 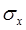, маловероятное событие. Данный критерий надежен при числе измерений n>20 и широко применяется. Практические вычисления проводят следующим образом:

1. Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее либо наименьшее значение наблюдения измеряемой величины.

2. Вычисляют среднее арифметическое значение выборки 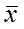без учета сомнительного значения 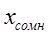измеряемой величины.

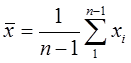
3. Вычисляют оценку СКО выборки 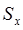без учета сомнительного значения 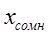измеряемой величины.

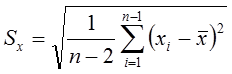
4. Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.

Если 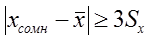, то сомнительное значение отбрасывают, как промах.

Если 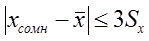, то сомнительное значение оставляют как равноправное в ряду наблюдений.

Данный метод «трех сигм» среди метрологов является самым популярным, достаточно надежным и удобным, так как при этом ни каких таблиц под рукой иметь нет необходимости.

Критерий Романовского применяется, если число измерений n<20 . При этом вычисляется соотношение

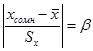
и сравнивается с табличным критерием 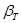по таблице 7. Если 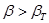сомнительное значение x_сомн отбрасывают как промах. Если 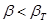сомнительное значение оставляют как равноправное в ряду наблюдений.

Таблица 7

Значение критерия Романовского

Значимость, q	Число измерений
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,09	2,00	2,17	2,29	2,39	2,49	2,62

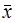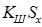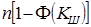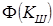Критерий Шарлье– используется, если число наблюдений велико, n>20 . Тогда по теореме Бернулли число результатов наблюдений, превышающих по абсолютному значению среднее арифметическое значение на величину будет равно , где - значение функции Лапласа (нормального нормированного распределения) для 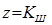. Если сомнителен в ряду наблюдений один результат, то 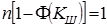. Отсюда

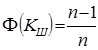
Если 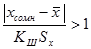то сомнительное значение x_сомн отбрасывают как промах.

Если 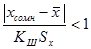то сомнительное значение x_сомн оставляют как равноправное в ряду наблюдений.

Таблица 8

Значение критерия Шарлье

Число наблюдений
	1,96	2,13	2,24	2,32	2,58

Критерий Диксона является достаточно универсальным в смысле числа наблюдений и применяется для выборки с небольшим количеством наблюдений. Практические вычисления проводят следующим образом:

1. Задаются критерием значимости q .

2. Ряд наблюдений записывают в вариационный ряд (например, возрастающий) 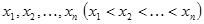. Сомнительным значением в данном случае должно быть значение с наибольшим порядковым номером, т.е. .

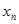3. Вычисляют критерий Диксона 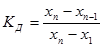, который будет всегда положительным числом.

4. Из таблицы 8 находят критическое значение критерия Диксона 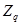(критическая область для критерия Диксона )

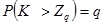Если 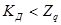сомнительное значение 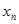отбрасывают как промах.

Если 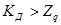сомнительное значение 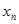оставляют как равноправное в ряду наблюдений.

Таблица 9

Значение критерия Диксона

Число наблюдений	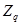при уровне значимости q равном
0,10	0,05	0,02	0,01
	0,68	0,70	0,85	0,89
	0,48	0,56	0,64	0,70
	0,40	0,47	0,54	0,59
	0,35	0,41	0,48	0,53
	0,29	0,35	0,41	0,45
	0,28	0,33	0,39	0,43
	0,26	0,31	0,37	0,41
	0,25	0,30	0,36	0,39
	0,22	0,26	0,31	0,34