Расчет коэффициента преступности
Этапы статистического исследования. Их краткая характеристика.
Статистическое исследование включает в себя 3 основных этапа:
1.Статистическое наблюдение - формируются первичные статистические данные, или исходная статистическая информация, которая является основой статистического исследования. Если при сборе первичных статистических данных допущена ошибка или материал оказался недоброкачественным, это повлияет на правильность и достоверность как теоретических, так и практических выводов;
2.Сводка и группировка данных - на этой стадии совокупность делится по признакам различия и объединяется по признакам сходства, подсчитываются суммарные показатели по группам и в целом. С помощью метода группировок изучаемые явления в зависимости от существенных признаков подразделяются на типы, группы и подгруппы. Метод группировок позволяет ограничивать качественно однородные в существенном отношении совокупности, что служит предпосылкой для определения и применения обобщающих показателей;
3.Обработка и анализ полученных данных, выявление закономерностей. На этом этапе с помощью обобщающих показателей рассчитываются относительные и средние величины, дается сводная оценка вариации признаков, характеризуется динамика явлений, применяются индексы, балансовые построения, рассчитываются показатели, характеризующие тесноту связей в изменении признаков. С целью наиболее рационального и наглядного изложения цифрового материала он представляется в виде таблиц и графиков.
Все этапы статистического исследования тесно связаны друг с другом и одинаково важны. Недостатки и ошибки, возникающие на каждой стадии, сказываются на все исследовании в целом. Поэтому правильное использование специальных методов статистической науки на каждом этапе позволяет получить достоверную информацию в результате статистического исследования.
Методы статистического исследования:
-Статистическое наблюдение;
-Сводка и группировка данных;
-Расчет обобщающих показателей (абсолютные, относительные и средние величины);
-Статистические распределения (вариационные ряды);
-Выборочный метод;
-Корреляционно-регрессионный анализ;
-Ряды динамики;
-Индексы.
Задача статистики – исчисление статистических показателей и их анализ, благодаря чему управляющие органы получают всестороннюю характеристику управляемого объекта.
Расчет коэффициента преступности.
Коэффициент преступности – это количество преступлений и лиц, их совершивших на определенное количество населения.
Коэффициенты исчисляются путем сопоставления сведений о преступности с данными о населении.
Коэффициенты бывают:
если сопоставляются данные о числе зарегистрированных преступлений, то используется коэффициент Кф (коэффициент по фактам),
если сопоставляются сведения о числе выявленных преступников, то используется Кл (коэффициент по лицам),
если же сопоставляются показатели о числе осужденных – коэффициент Ко(коэффициент по количеству осужденных).
Формула расчетобщего коэффициента преступности на 100 тысяч человек:
К = П х 100 000 / Н,
где К – коэффициент преступности
П – число фактов или количество лиц, совершивших преступления
Н – численность населения (всего или в соответствующем возрасте).
Можно рассчитать коэффициент и на 10 тысяч человек, при необходимости – на 1 тысячу человек.
Коэффициент преступности может рассчитываться либо на все население, либо на населения в возрасте уголовной ответственности (в России – на население в возрасте с 14 лет и старше).
Когда расчет делается на все население, коэффициент фактически отражает лишь то, как население страдает от преступности. Коэффициент, рассчитанный на население в возрасте от 14 лет и старше, показывает криминальную активность населения возраста уголовной ответственности, то, насколько интенсивно оно продуцирует преступное поведение.
3. Расчет удельного веса.
Расчет удельного веса отдельного вида преступности делается в криминологии, исходя из структуры преступности для данного территориального образования. Структура преступности является важнейшим для вникания в суть происходящих процессов понятием, она определяется соотношением (удельным весом) в преступности ее видов, групп преступлений, классифицируемых по уголовно-правовым или же криминологическим основаниям, к которым относят: социальную и мотивационную направленность; социально-территориальную распространенность; социально-групповой состав; степень и характер общественной опасности; устойчивость преступности; степень организованности и некоторые другие признаки, учитывающие внешние и внутренние характеристики преступности.
Для того чтобы провести анализ структуры преступности, необходимо определить процентное соотношение преступлений особо тяжких, тяжких, средней и небольшой тяжести; умышленных и неосторожных, а также удельный вес рецидивной, профессиональной, групповой преступности; долю t преступности несовершеннолетних, женской преступности и т. п. Для полноты криминологической картины имеет значение также характер мотивации личности преступника (выделяют насильственные, корыстные и корыстно-насильственные преступления).
Для определения удельного веса отдельного типа, рода, вида или разновидности преступности (С)используется следующая формула:
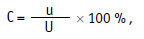
где u – показатель объема отдельного типа, рода, вида или разновидности преступности; U – показатель объема всей преступности на той же территории за тот же период времени.
Удельный вес отдельного типа, рода, вида или разновидности преступности показывает, какую долю в общей преступности данного территориального образования составляет какой-то определенный вид преступлений. Исходя из общей картины, можно сделать вывод, с чем связан рост или снижение таких преступлений, какие группы населения оказываются вовлеченными, как лучше построить профилактическую работу.
4. Относительные величины динамики.
Относительные величины динамики характеризуют изменение изучаемого явления во времени, выявляют направление развития, измеряют интенсивность развития. Рассчитывается относительная величина динамики как отношение уровня признака в определенный период или момент времени к уровню того же признака в предшествующий период или момент времени, т. е. характеризует изменение уровня определенного явления во времени.
Относительные величины вычисляются как отношение двух чисел. При этом числитель называется сравниваемой величиной, а знаменатель – базой относительного сравнения. В зависимости от характера изучаемого явления и задач исследования базисная величина может принимать различные значения, что приводит к различным формам выражения относительных величин. Относительные величины измеряются:
• в коэффициентах: если база сравнения принята за 1, то относительная величина выражается целым или дробным числом, показывающим, во сколько раз одна величина больше другой или какую часть ее составляет;
• в процентах, если база сравнения принимается за 100;
• в промилле, если база сравнения принимается за 1000;
• в продецимилле, если база сравнения принимается за 10 000;
• в именованных числах (км, кг, га) и др.
В каждом конкретном случае выбор той или иной формы относительной величины определяется задачами исследования и социально-экономической сущностью, мерой которого выступает искомый относительный показатель. По своему содержанию относительные величины подразделяются на следующие виды: выполнения договорных обязательств; динамики; структуры; координации; интенсивности; сравнения.
5. Расчет среднегодового темпа прироста (снижения).
Для характеристики среднего относительного изменения признаков правовых и юридически значимых явлений рассчитывают интегрированные относительные показатели роста или снижения уровня признака - среднегодовые темпы роста и прироста (сокращения).
Среднегодовой темп роста характеризует среднее относительное изменение состояния (уровня) явления за рассматриваемый период времени в целом и рассчитывается по формуле:
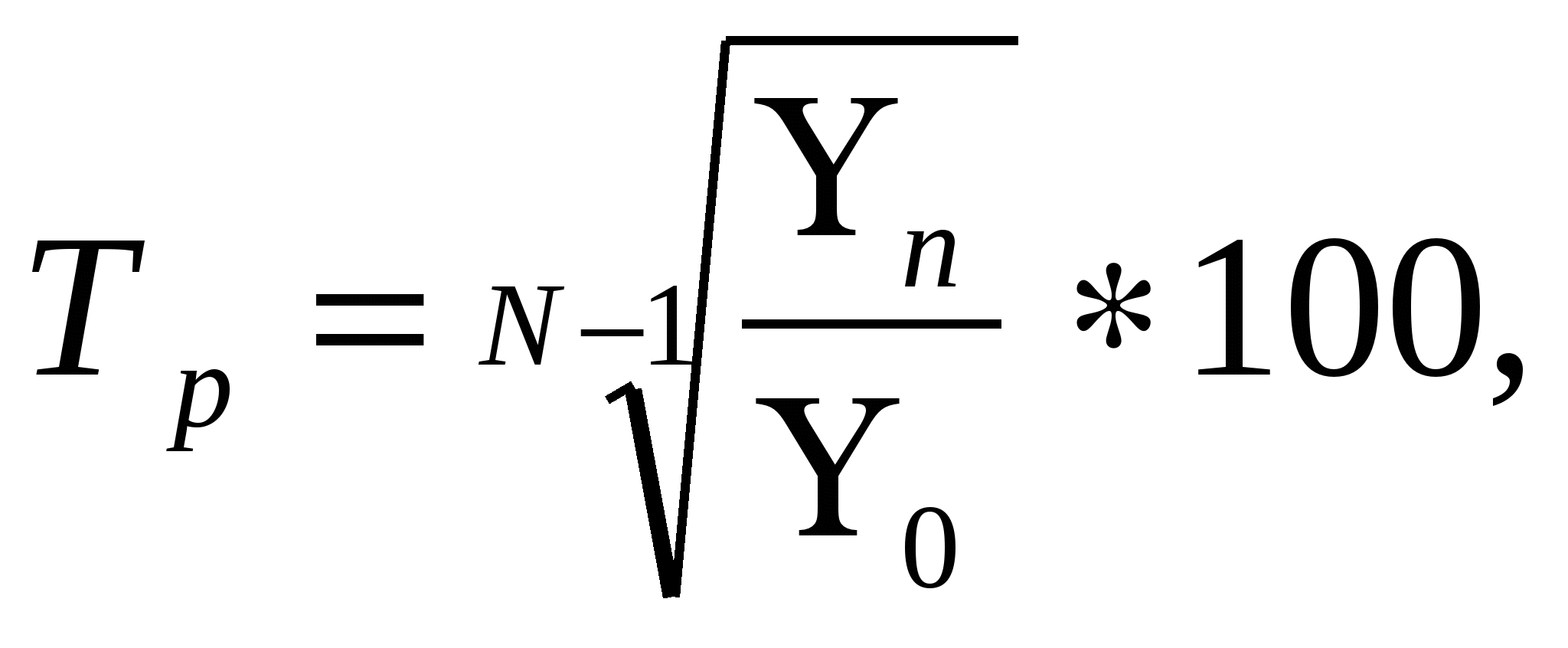
где Yn - последний уровень ряда динамики параметра явления,
Yo - уровень ряда динамики параметра явления,
n - число уровней в ряду динамики.
Среднегодовой темп прироста характеризует среднюю величину относительного прироста параметра явления за рассматриваемый период времени в целом и рассчитывается на основе среднегодового темпа роста путем вычитания из последнего 100%:
Тпр = Тр - 100%
Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста - отрицательной величиной. Отрицательный темп прироста представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня явления.
6. Расчет коэффициента раскрываемости преступлений.
Основными показателями преступности являются:
1) состояние преступности – количество преступлений и лиц, их совершивших, на определенной территории за определенное время;
2) коэффициент, или уровень, преступности – общее число учтенных преступлений за определенное время и на определенной территории.
К = (П / Н) ЧБ,
где К– уровень преступности; П– количество преступлений; Н– численность населения, достигшего возраста наступления уголовной ответственности, проживающего на территории, для которого рассчитывается коэффициент; Б– коэффициент (обычно 100,000);
3) структура преступности – раскрывается через ее внутреннее содержание – соотношение в общем массиве преступлений и преступников, различных их видов и категорий, выделенных по тем или иным правовым, криминологическим основаниям.
4) динамика преступности – изменения преступности (состояния, уровня, структуры и т. д.) во времени.
Коэффициент раскрываемости преступлений рассчитывается как отношение числа раскрытых деяний в отчетном году к числу расследуемых в том же отчетном периоде.
7. Расчет индекса тяжести преступлений.
Особый интерес для юристов уголовно-правовой специализации представляют индексы, отражающие степень общественной опасности (тяжести) разных преступлений, совершаемых в разных регионах или в разные годы. Они рассчитываются на основе общего числа учтенных деяний, санкций за их совершение и других признаков, влияющих на общественную опасность (тяжесть) преступлений. Для количественного измерения тяжести преступлений по некой условной шкале предлагалось учитывать меру наказания, либо реально назначенную судом, либо указанную в санкциях статей Особенной части УК.
Для расчета индекса тяжести совокупности преступленийприведем условный пример. Предположим, в городе N в 1995 г. было совершено 30 умышленных убийств (ч. 2 ст. 105), 15 изнасилований (ч. 2 ст. 131), 200 хулиганств (ч. 2 ст. 213), 40 разбоев (ч. 2 ст. 162) и 100 краж (ч. 2 ст. 158), а в 1996 г. были совершены соответственно те же Деяния, но в ином количестве: 25,20,250,30 и 150. Произведение числа Совершенных преступлений по видам на их баллы (индивидуальный индекс) даст условное число преступлений, которое можно поименовать видовым индексом.
Используя формулу агрегатного индекса, применяемого в экономике, для криминологических нужд можно записать ее следующим образом:
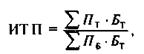
где ИТП — индекс тяжести преступлений;
Пт — сумма преступлений текущего периода;
Бт — баллы тяжести преступлений (они должны быть одни и для текущего, и для базового периода и представляют собой максимальные сроки уголовного наказания по каждой категории деяний, т.е. 2, 5, 10 и 20 лет лишения свободы); Пб — сумма преступлений базового периода.
Подставив в формулу наши условные данные, получим искомый индекс:
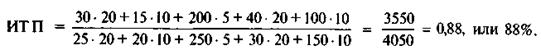
Полученный агрегированный показатель означает, что в 1996 г. индекс тяжести преступлений понизился (1 - 0,88) по сравнению с аналогичным показателем 1995 г. на 0,12 (или на 12%), хотя число совершенных преступлений в 1996 г. увеличилось с 385 до 475, т.е. на 23,4%. Подобные сравнения можно сделать по данным одного года, но разных регионов. Полученный показатель может свидетельствовать не только о количестве, но и о качестве правоохранительной деятельности. По агрегированным индексам, например, при равном числе учтенных преступлений можно судить о том, за счет чего формируется в том или ином регионе регистрируемый уровень преступности. Если при равенстве учтенных деяний в сопоставляемых субъектах Федерации в одном из них агрегированный индекс выше, чем в другом, т.е. достаточные основания полагать, что в первом регионе либо реальная преступность сдвинута к тяжким формам, либо учет ее направлен лишь на тяжкие деяния.
Использование индекса тяжести преступлений для пространственных и временных сравнений поможет более объективно оценить реальную криминологическую обстановку в стране, регионе, городе или любом ином населенном пункте либо установить эффективность борьбы с ней со стороны правоохранительных органов.
Расчет среднего арифметического для дискретного ряда.9. Расчет среднего арифметического взвешенного для дискретного ряда.10. Расчет среднего арифметического для интервального ряда.
Средняя арифметическая - самый распространенный вид средней величины. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных единиц совокупности. Ее расчет является наиболее простым: складывают величины всех вариантов и делят эту сумму на общее число единиц вариантов.
Предположим, что годовая нагрузка 15 судей городского суда, специализирующихся на рассмотрении гражданских дел различной направленности, составила: 17, 42, 47, 47, 50, 50, 50, 63, 68, 68, 75, 78, 80, 80, 85. Необходимо исчислить среднюю годовую нагрузку на одного судью (х - средняя арифметическая) в целях сравнения со средней общефедеральной и краевой (областной, республиканской). Для этого надо сложить значения всех индивидуальных нагрузок (которые обозначим: xv х2, хг ..., хп) и разделить на общее число судей («):
Хцрифн -
_ х1+х2+х3+...+х„
17 + 42 + 47+47
900 15
= 60.
Таким путем мы получили простую среднюю арифметическую величину. В рассматриваемом примере 15 вариант (15 индивидуальных нагрузок), но они имеют всего лишь 10 значений, так как у некоторых судей нагрузки были одинаковыми: 47 и 47; 50, 50 и 50; 68 и 68; 80 и 80. В этом случае исчислять среднюю арифметическую можно проще: перед суммированием вариант нужно умножить варианты (х,, хг х3, ...) на соответствующее число частот (/J, fv fy ...), затем полученные произведения сложить (!х/) и разделить на общее число судей (If). Нагляднее всего это можно сделать в таблице (табл. 1), в которой число судей распределяется по числу рассмотренных дел, что и представляет собой дискретный (от лат. discretus — прерывистый) вариационный ряд.
Таблица 1 Вычисление средней нагрузки судей (по формуле средней арифметической)
| Число дел (варианта х) | Число судей (частота/) | Произведение вариант на частоты (xf) |
| 17 • 1 = 17 | ||
| 42 • 1 = 42 | ||
| 47 • 2 = 94 | ||
| 50 • 3 = 150 | ||
| 63 • 1 = 63 | ||
| 68 • 2 = 136 | ||
| 75 • 1 = 75 | ||
| 78 • 1 = 78 | ||
| 80 • 2 = 160 | ||
| 85 • 1 = 85 | ||
| £х= 605 | £/= 15 | Ух = 900 |
Средняя арифметическая для дискретного вариационного ряда исчисляется по формуле средней арифметической взвешенной. Для нашего примера
средняя арифметическая взвешенная не имеет принципиальных отличий от простой средней арифметической. В ней суммирование одного и того же значения заменено умножением этого значения на его частоту, т. е. в этом случае каждое значение (варианта) взвешивается по частоте встречаемости. Наш пример прост и технические выгоды от применения средней взвешенной не так очевидны. Но когда частоты исчисляются сотнями или тысячами, то применение средней взвешенной намного упрощает расчет.
При расчете простой средней арифметической часто вовсе не обязательно знать величину каждого индивидуального значения (варианты) или иметь в своем распоряжении построенный на основе этих вариант вариационный ряд. В официальной отчетности юридических учреждений, как правило, уже имеются многие суммарные величины. Это суммирование происходит последовательно в районах (городах), субъектах Федерации и в центре при сводке и группировке данных, полученных из документов первичного учета.
Открываем отчет о работе прокурора (Ф. П) за 1996 г. В разделе 4 (участие прокурора в рассмотрении гражданских и арбитражных дел в судах) в таблице Б (иски (заявления) прокурора) указано, что в 1996 г. прокурорами было предъявлено 170 882 иска на сумму 1 553 749 млн рублей. На основе этих обобщенных данных мы можем сразу рассчитать среднюю арифметическую сумму, приходящуюся на один предъявленный иск (имущественного и неимущественного характера):
Используя другие обобщенные данные, можно рассчитать, что средняя сумма по искам различных видов была:
- 16 270 728 руб. (в имущественных интересах граждан);
- 10 741 826 руб. (в имущественных интересах государства);
- 5 718 097 руб. (связанных с хищениями);
- 4 678 344 руб. (связанных с производственным травматизмом);
— 5 840 399 руб. (связанных с незаконными увольнениями); - 17 375 765 руб. (связанных с нарушениями законов об охране природы).
Расчет средней на основе обобщенных в отчетах данных возможен и тогда, когда каждое отдельное значение варианты вообще не фиксируется. Например, средняя урожайность на гектар может быть подсчитана путем деления валового сбора зерна на посевную площадь, хотя никто не подсчитывает урожай на каждом гектаре. Этим же способом можно подсчитать среднее число совершенных преступлений на 1 кв. километр или на 10 тыс., 100 тыс. жителей. Последний средний арифметический показатель смыкается с относительным показателем интенсивности преступности (коэффициентом преступности).
Между средними (особенно средней арифметической) и относительными величинами иногда не существует четких и однозначных границ. И те и другие являются обобщающими. Более того, любая средняя величина — это своеобразное отношение двух абсолютных величин, т. е. она одновременно представляет собой и определенную относительную величину (в нашем последнем примере — отношение общей суммы исков к их числу). С другой стороны, любая относительная величина дает своеобразную усредненную характеристику явления. Например, отношения динамики дают усредненную характеристику роста или снижения уровня изучаемого явления за анализируемые годы; отношения распределения — усредненный удельный вес какого-то показателя в структуре всех показателей и т. д. Однако при этом нельзя не видеть их статистически значимых различий, о которых говорилось в понятии о средних.
Некоторые особенности и трудности при расчете средней арифметической имеются для интервального ряда статистических показателей, т.е., когда индивидуальные численные значения (варианты) сгруппированы в интервалы (от — до). В юридической статистике интервальные ряды используются чаще, чем дискретные. Так учитываются сроки наказания, сроки следствия, сроки рассмотрения уголовных и гражданских дел, возраст правонарушителей и т. д.
В отчете Минюста РФ (Ф. 10) о числе привлеченных к уголовной ответственности и мерах уголовного наказания за 1996 г. меры наказания зафиксированы в виде интервального ряда. Попытаемся рассчитать средний срок лишения свободы на одного осужденного за умышленное убийство при отягчающих обстоятельствах (табл. 2).
Таблица 2 Вычисление срока наказания за умышленное убийство для интервального ряда
| Сроки лишения свободы (х) | Число осужденных (/) | Середина интервалов (/) | Произведение середины интервалов и частоты {/?) |
| До 1 года | 0,5 | ||
| Свыше 1 года до 2 лет | 1,5 | 4,5 | |
| Свыше 2 до 3 лет | 2,5 | ||
| Свыше 3 до 5 лет | |||
| Свыше 5 до 8 лет | 6,5 | ||
| Свыше 8 до 10 лет | 11 331 | ||
| Свыше 10 до 15 лет | 12,5 | 36 512,5 | |
| J/= 4803 | Ifl= 51 559 |
Если бы ряд был дискретный, то расчет средней можно было бы произвести по формуле средней арифметической взвешенной. Но этого сделать нельзя, так как точные сроки наказания убийц неизвестны. Они обобщены в интервалах «от— до». Это можно сделать при одном условии, если допустить, что внутри каждой группы «от— до» сроки лишения свободы распределены равномерно и середина интервала — это среднее значение для данной группы. Середина интервала рассчитывается по формуле средней арифметической путем деления на 2 суммы двух границ интервала. К примеру:
8 лет + 10 лет 18 лет .
В действительности средняя арифметическая середины интервалов может и не отражать среднего значения сроков лишения свободы в том или ином интервале. Но другого выхода нет, так как отсутствует учет индивидуальных сроков лишения свободы в статистической отчетности судов. Поэтому условно приняв середину интервалов за среднее значение варианты каждой группы «от— до» (см. графу 3 табл. 2), мы можем рассчитать средний срок лишения свободы для убийц по формуле средней взвешенной:
При расчете средней арифметической для интервального ряда встречается и другая трудность, когда у первой группы может не быть нижней границы интервала (в нашем примере — до 1 года, а нижний предел не указан), у последней группы может, не быть верхней границы интервала (например, свыше 10 лет, а верхний предел также не указан). При таких неопределенных интервалах их границы либо устанавливают произвольно, либо определяют их на основе дополнительных изучений. В нашем примере можно обратиться к ст. 56 УК РФ, где установлен минимальный (шесть месяцев) и максимальный (20 лет) сроки лишения свободы.
Мы живем во время, когда компьютер становится неотъемлемым аппаратом любой аналитической деятельности. В этих условиях исчисление любых средних величин упрощается путем использования необходимых компьютерных программ. Тем не менее, мы подробно излагаем технику вычисления, полагая, что любой юрист (практик или ученый) должен понимать сущность производимых расчетов и уметь их произвести любым доступным способом. С целью упрощения таких расчетов можно использовать некоторые свойства средней арифметической, которые мы приводим без доказательств.
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. xLf= Ixf. В первом нашем примере: 60 дел • 15 судей = 900.
2. Если от каждой варианты отнять (или прибавить к ней) одно и то же число, то новая средняя уменьшится (или увеличится) на то же число. Это означает, что в целях упрощения расчетов можно уменьшить на произвольное число все варианты, рассчитать среднюю и, прибавив к ней то самое произвольное число, получить ее реальную величину.
3. Если каждую варианту разделить (или умножить) на какое-либо произвольное число, то средняя арифметическая уменьшится (или увеличится) во столько же раз. Это правило также можно использовать для облегчения расчетов средней арифметической.
4. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. Это обусловлено тем, что частоты при исчислении средней арифметической имеют значение веса не как абсолютные данные, а как удельные веса вариант в вариационном ряду. Поэтому и при увеличении, и при уменьшении в одинаковой степени их доли в вариационном ряду не меняются.
5. Сумма отклонений вариант от средней арифметической всегда равна нулю. Иначе это свойство формулируется следующим образом: сумма положительных отклонений от средней равна сумме отрицательных отклонений, т. е. в средней арифметической и положительные, и отрицательные отклонения от нее взаимопогашаются.
6. Общая средняя равна средней из частных средних, взвешенной по численности соответствующих частей совокупности. Если известно, что среднее число уголовных дел, приходящихся на одного следователя в год в одном субъекте Федерации, равно 68, в другом — 72, в третьем — 74, причем в первом числится 180 следователей, во втором — 160, а в третьем — 150, то общую среднюю для региона можно подсчитать таким образом:
_ 68-180 + 72-160 + 74 150 180 + 160 + 150
• = 71,1 дел.
11. Понятия моды и медианы. Расчет моды и медианы дискретного ряда.
Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.
Мода и медиана в отличии от степенных средних являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.
Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров и т.д., в этих случаях прибегают к моде.
Медиана интересна тем, что показывает количественную границу значение варьирующего признака, которую достигла половина членов совокупности. Пусть средняя заработная плата работников банка составила 650000 руб. в месяц. Эта характеристика может быть дополнена, если мы скажем, что половина работников получила заработную плату 700000 руб. и выше, т.е. приведем медиану. Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности
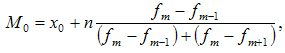
где:
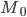— значение моды
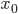— нижняя граница модального интервала
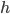— величина интервала
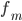— частота модального интервала
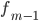— частота интервала, предшествующего модальному
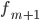— частота интервала, следующего за модальным
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот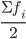 
, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
12. Расчет среднего арифметического отклонения.
Отклонения от средней всех значений признака в вариационном ряду можно получить, если рассчитать отклонения всех вариант от средней
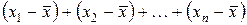и вычислить среднюю арифметическую из всех отклонений.
Сумма всех положительных (которые больше средней) и всех отрицательных (которые меньше средней) отклонений равна нулю. Поэтому при расчете средней арифметической из отклонений необходимо абстрагироваться от знаков «+» и «-». В этом случае сумма отклонений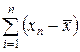 
, разделенная на число отклонений 
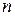, а при наличии частот - на число 
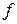, и будет средним арифметическим отклонением. В связи с этим расчетная формула будет выглядеть следующим образом:
.
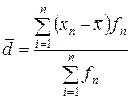В результате мы получили среднее арифметическое (линейное) отклонение, которое обозначается символом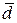 
.
13. Расчет среднего квадратического отклонения.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
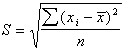— среднее квадратическое отклонение невзвешенное;
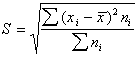— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (напр. в процентах).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
14. Расчет среднего геометрического отклонения.
Среднее геометрическое позволяет оценить степень изменения переменной с течением времени. Среднее геометрическое — это корень n-й степени из произведения n величин:
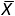G= (X1* X2* … * Xn)1/n
Для расчетов средней геометрической простой используется формула:
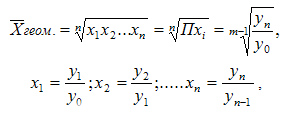
где:
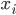— цепной коэффициент роста
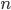— число этих коэффициентов роста
П — знак произведения
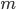— количество уровней ряда
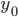— значение начального уровня ряда
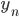— значение конечного уровня ряда
Для определения средней геометрической взвешенной применяется формула:
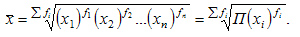
15. Расчет дисперсии.
Дисперсия, или средний квадрат отклонений - обозначается символом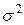 
(сигма малая в квадрате) и представляет собой то же среднее арифметическое отклонение 
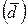, но только отклонения возведены в квадрат, и из квадратов отклонений вычисляют среднюю величину:
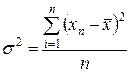, а при наличии частот 
.
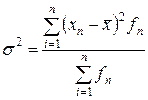При расчете дисперсии не надо абстрагироваться от знаков (+ и -) отклонений, так как при возведении в квадрат все знаки отклонений становятся положительными.