Действия над векторами в координатной форме.
Даны векторы  ={ax, ay, az} и
={ax, ay, az} и  ={bx, by, bz}.
={bx, by, bz}.
1. (  ±
±  )={ax ± bx, ay ± by, az ± bz}.
)={ax ± bx, ay ± by, az ± bz}.
2. l  ={lax, lay, laz}, где l – скаляр.
={lax, lay, laz}, где l – скаляр.
Скалярное произведение векторов.
Определение:Под скалярным произведением двух векторов 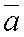 и
и 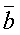
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. 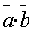 =
= 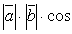
 ,
,  - угол между векторами
- угол между векторами 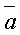 и
и 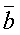 .
.
Свойства скалярного произведения:
1. 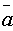 ×
× 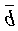 =
= 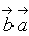

2. ( 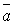 +
+ 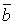 )
) 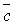 =
= 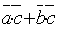
3. 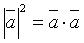
4. 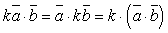
5. 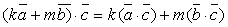 , где
, где 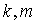 – скаляры.
– скаляры.
6. два вектора перпендикулярны (ортогональны), если 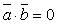 .
.
7. 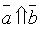 тогда и только тогда, когда
тогда и только тогда, когда 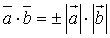 .
.
Скалярное произведение в координатной форме имеет вид: 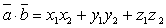 ,где
,где 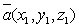 и
и 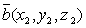 .
.
Пример:Найти скалярное произведение векторов 
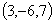 и
и 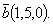
Решение: 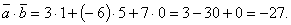
Векторное проведение векторов.
Определение: Под векторным произведением двух векторов 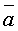 и
и 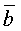 понимается вектор,
понимается вектор, 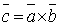 для которого:
для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е. 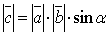 , где
, где 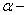 угол между векторами
угол между векторами 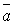 и
и 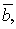
-этот вектор перпендикулярен перемножаемым векторам, т.е. 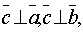
-если векторы 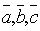 неколлинеарны, то они образуют правую тройку векторов.
неколлинеарны, то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 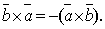
2.Векторный квадрат равен нуль-вектору, т.е. 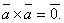
3.Скалярный множитель можно выносить за знак векторного произведения, т.е. 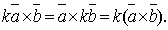
4.Для любых трех векторов 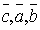 справедливо равенство
справедливо равенство 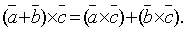
5.Необходимое и достаточное условие коллинеарности двух векторов 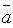 и
и 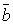 :
: 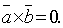
Векторное произведение в координатной форме.
Если известны координаты векторов 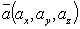 и
и 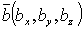 ,то их векторное произведение находится по формуле:
,то их векторное произведение находится по формуле:
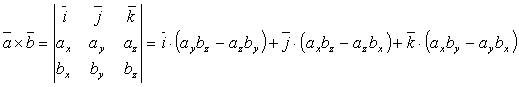 .
.
Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах 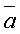 и
и 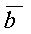 , вычисляется по формуле:
, вычисляется по формуле:
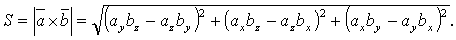
Пример:Вычислить площадь треугольника с вершинами 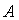 (1;-1;2),
(1;-1;2), 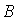 (5;-6;2),
(5;-6;2), 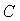 (1;3;-1).
(1;3;-1).
Решение: 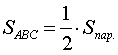 .
.
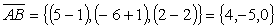 ,
, 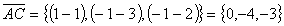 , тогда площадь треугольника АВС будет вычисляться следующим образом:
, тогда площадь треугольника АВС будет вычисляться следующим образом:
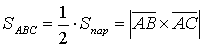 ,
,

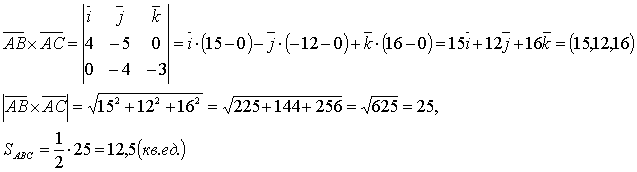
Смешанное произведение векторов.
Определение:Смешанным (векторно-скалярным) произведением векторов 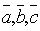 называется число, определяемое по формуле:
называется число, определяемое по формуле: 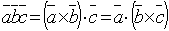 .
.
Свойства смешанного произведения:
1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. 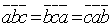 .
.
2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. 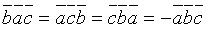 .
.
3.Необходимое и достаточное условие компланарности трех векторов 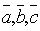 :
: 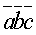 =0.
=0.
4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. 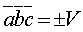 .
.
Если известны координаты векторов 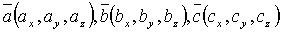 ,то смешанное произведение находится по формуле:
,то смешанное произведение находится по формуле: 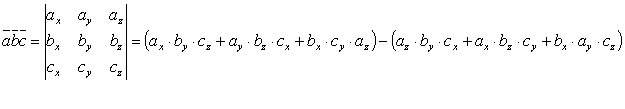
Пример:Вычислить смешанное произведение векторов 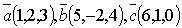 .
.
Решение: 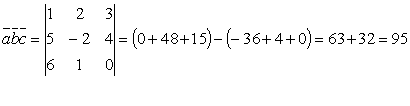
Базис системы векторов.
Определение.Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространствуR.
Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.
Пример. 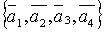
Определение. Любой вектор вида 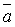 =
= 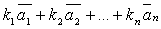 называется линейной комбинацией векторов
называется линейной комбинацией векторов 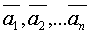 . Числа
. Числа 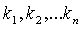 - коэффициентами линейной комбинации.
- коэффициентами линейной комбинации.
Пример. 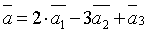 .
.
Определение. Если вектор 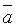 является линейной комбинацией векторов
является линейной комбинацией векторов 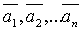 , то говорят, что вектор
, то говорят, что вектор 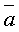 линейно выражается через векторы
линейно выражается через векторы 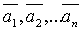 .
.
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.
Пример. Система векторов 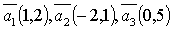 линейно-зависима, т. к. вектор
линейно-зависима, т. к. вектор 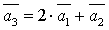 .
.
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства 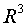 :
: 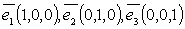 .
.
2. В системе векторов 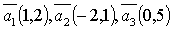 базисом являются векторы:
базисом являются векторы: 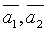 , т.к.
, т.к. 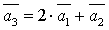 линейно выражается через векторы
линейно выражается через векторы 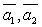 .
.
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
