Оценка остатка знакопеременного ряда
Пусть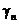 
есть остаток знакопеременного ряда после п-го слагаемого.
Пусть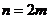 
. Тогда имеем:
.
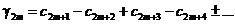Проделаем с этим выражением преобразования, аналогичные тем, которые проделывались с частными суммами. Группируя слагаемые так
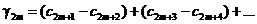
получаем, что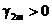 
. Группируя слагаемые так
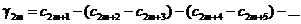
получаем, что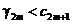 
. Окончательно имеем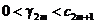 
Пусть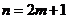 
. Тогда имеем:
.
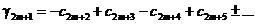Но тогда
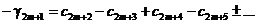
и все предыдущие рассуждения повторяются слово в слово. В этом случае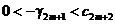 
.
Оба полученных неравенства можно объединить в одно
.
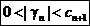Словами его часто формулируют так: остаток знакопеременного ряда меньше первого отброшенного слагаемого.
Сходимость рядов с произвольными слагаемыми.
Пусть теперь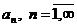 
есть вещественные числа произвольного знака. Рассмотрим критерии сходимости ряда 
.
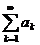Признак сходимости Больцано-Коши
Для сходимости ряда 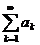необходимо и достаточно, чтобы
.
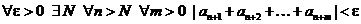Доказательство.
Сходимость ряда 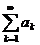, по определению, означает существование конечного предела его частных сумм 
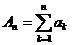. Но, по признаку Больцано-Коши для последовательности, для существования такого предела необходимо и достаточно, чтобы
.
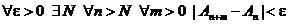Но легко видеть, что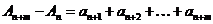 
, что и дает доказываемый признак. <
Следствие. Если сходится ряд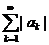 
, то сходится и ряд .
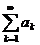Доказательство. В приводимой ниже цепочке следований два раза идет ссылка на признак сходимости Больцано-Коши
Ряд 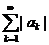сходится Þ по признаку Больцано-Коши
.
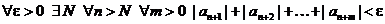Но тогда
< 
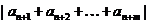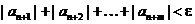Þ
по тому же признаку ряд 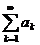сходится. <
Определение. Если ряд 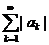сходится, то ряд 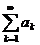называется абсолютно сходящимся рядом.Если ряд 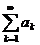сходится, но 
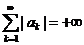, то ряд 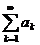называется неабсолютно сходящимся рядом.
Пример неабсолютно сходящегося ряда.
Таким рядом является, например, ряд
,
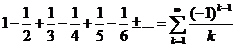который сходится по признаку Лейбница. Но ряд, составленный из модулей
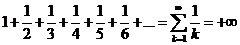
расходится, как гармонический ряд с s = 1.
Признак Больцано-Коши не является рабочим признаком, но на его основе строятся рабочие признаки. Но, прежде, чем переходить к их изложению, рассмотрим один вспомогательный вопрос.
Преобразование Абеля
Пусть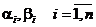 
есть некоторые вещественные числа и 
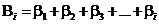. Тогда верна формула
.
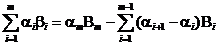Эта формула и называется преобразованием Абеля. Она является дискретным вариантом формулы интегрирования определенных интегралов по частям.
Доказательство.
Имеем
; 
; 
; … ; 
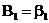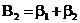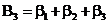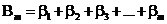
Отсюда
; 
; 
; 
; …; 
.
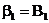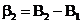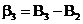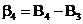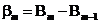Теперь имеем следующую цепочку преобразований:
. <
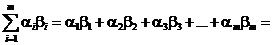
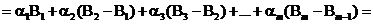
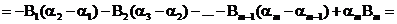
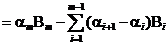Признак Дирихле
Пусть
1. Все частные суммы ряда 
ограничены, то есть 
;
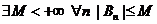2. 
.
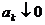Тогда ряд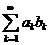 
сходится.
Доказательство.
1. Согласно первому ограничению мы имеем
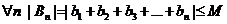
Пусть
.
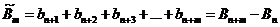Тогда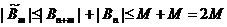 
.
2. 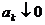Þ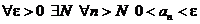 
.
3. Считая, что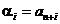 
, 
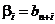, а также, что 
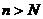и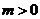 
используем преобразование Абеля. Получаем (вначале особых пояснений не требуется):
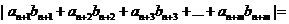(делаем преобразование Абеля)
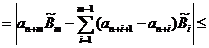
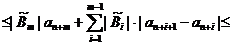
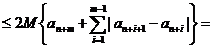
И тут наступает самый тонкий момент вывода. Вспомним, что, согласно ограничению 2,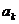 
монотонно убывают. Поэтому все разности вида 
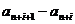отрицательны,то есть 
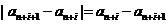. В силу этого
,
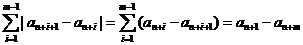и, продолжая прерванный вывод, получим:
.
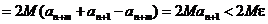Но e сколь угодно мало. Поэтому, со ссылкой на признак сходимости Больцано-Коши, можно утверждать, что ряд 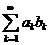сходится. <
Следствие. Если 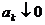,то сходятся ряды 
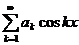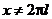(при 
) и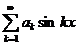 
(при любых х).
Доказательство.
Пусть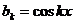 
. Начнем с известной со школы формулы
.
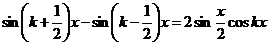Имеем
k = 1: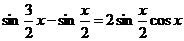 
;
k = 2: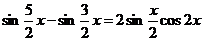 
;
k = 3: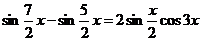 
;
……………..
k = n: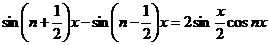 
.
Складывая все эти равенства, получим:
.
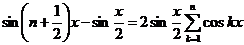Теперь мы имеем очень интересную формулу
.
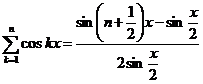Но тогда
,
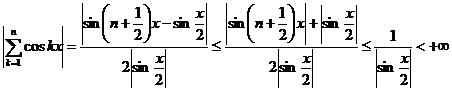если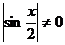 
, то есть, если 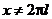. По признаку Дирихле, при 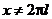ряд 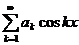сходится.
Для ряда 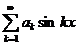все выкладки совершенно аналогичны, надо только начинать с формулы
.
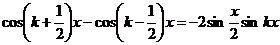Условие 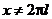можно убрать, так как при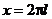 
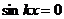и сумма ряда просто равна нулю.
Признак Абеля. Если ряд 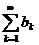сходится (не обязательно абсолютно!), а последовательность чисел 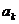монотонна и ограничена, то ряд 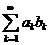сходится.
Доказательство.
1. Ряд 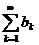сходится Þ по признаку Больцано-Коши
.
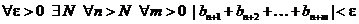2. Последовательность чисел 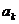ограничена Þ 
.
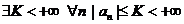3. Дальнейшие выкладки сначала полностью повторяют признак Больцано-Коши
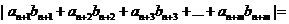(делаем преобразование Абеля)
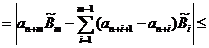
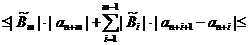
С этого момента начинаются отличия. Если раньше действовала оценка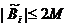 
, то теперь будет оценка 
:
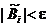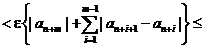
В этом месте - самый тонкий момент. Согласно ограничению, последовательность чисел 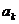монотонна Þ все разности 
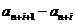одного знака, или все положительные, или все отрицательные. Поэтому можно записать
.
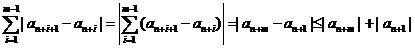Поэтому, продолжая доказательство, можно записать:
.
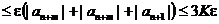Заключительная фраза та же самая: e сколь угодно мало. Поэтому, со ссылкой на признак сходимости Больцано-Коши, можно утверждать, что ряд 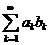сходится. <