Оценка остатка сходящегося ряда

При нахождении суммы ряда на ЭВМ, конечно, невозможно просуммировать бесконечное число слагаемых, всегда приходится ограничиваться какой-то частной суммой. Но при этом необходимо иметь какую-то оценку погрешности, то есть оценку остатка сходящегося ряда. Ниже будет получена одна из таких оценок.

Вспомним основное неравенство предыдущей теоремы:

.

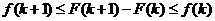Тогда имеем

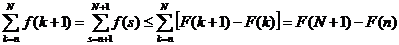
Переходя к пределу , получаем

.

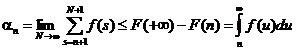С другой стороны получаем

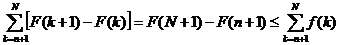
Переходя к пределу 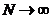, получаем

.

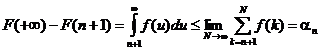Объединяя эти два неравенства, получаем окончательно

.

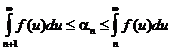Это и дает искомую оценку остатка сходящегося ряда.

Оценка темпа роста расходящегося ряда

Не следует думать, что расходящиеся ряды не имеют никакого смысла и их следует только выбросить. На практике иногда результат появляется в виде частной суммы расходящегося ряда, и возникает совсем другая проблема - оценить, как ведет себя эта сумма при большом числе слагаемых. Например, ответ на задачу появился в виде 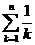. Ряд расходящийся, а ответ в виде «эта сумма стремится к бесконечности» никому не интересен. Что делать? Считать численно? Ну, при 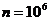эту сумму еще можно сосчитать, а что делать, если 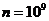? А ведь, скажем, число молекул бывает и побольше.

Поэтому и возникает проблема нахождение более удобных выражений (так называемых асимптотик) для частных сумм расходящихся рядов при большом числе слагаемых. Ниже будет выведена одна такая формула.

Итак, нам надо оценить поведение сумм вида 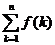при 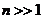. Мы построим такую оценку в тех предположениях о функции 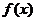, которые были сделаны выше.

Начинаем с основного неравенства

.

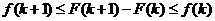Вычитаем из всех частей неравенства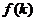

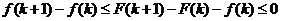
умножаем на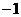

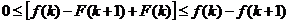
и складываем, меняя k от 1до п:

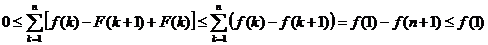
Обратите внимание на то, что, согласно предыдущему неравенству, все слагаемые в сумме 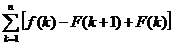положительны. Поэтому эта сумма монотонно возрастает с ростом п, но ее значения ограничены сверху величиной 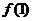. Ссылаясь на теорему о пределе монотонно возрастающей последовательности можно утверждать, что существует конечный

.

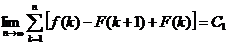А теперь отбросим этот предел. Но тогда мы обязаны в правой части добавить слагаемое, которое стремится к нулю и написать

,

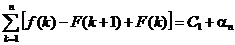где 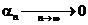, то есть 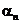является бесконечно малой величиной.

Теперь имеем

,

,

.

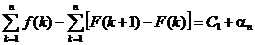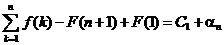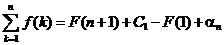Обозначая 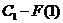через С, получаем окончательную формулу

,

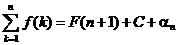или, в явном виде,

,

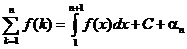правда константа С так и остается неопределенной и ее надо находить из каких-то других соображений.

Эта формула, являющаяся частным случаем гораздо более общей формулы, носящей название формулы Эйлера-Маклорена, и определяет асимптотику поведения частных сумм расходящегося ряда.

Пример.

Вернемся к 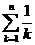. В данном случае, 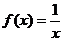, , 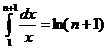и мы получим

.

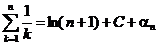В данном случае константа С (она носит название постоянной Эйлера) есть 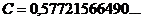Теперь можно считать эти суммы и при 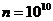! Вот только бы еще оценить …(ищи формулу Эйлера-Маклорена).

Знакопеременные ряды

Пусть имеется последовательность чисел 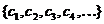, такая, что 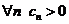. Ряд

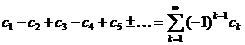
называется знакопеременным рядом.

Признак Лейбница. Если 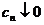, то ряд 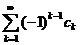сходится.

Доказательство.

Рассмотрим следующую частную сумму изучаемого ряда

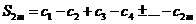
с чётныминдексом 2m. Ее можно записать двояко. Записывая ее в форме

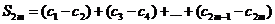
и вспоминая, что 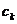монотонно убывают,получаем,что все слагаемые положительны и поэтому 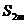монотонно возрастают с ростом m. С другой стороны, записывая эту же частную сумму в виде

,

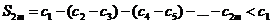так как все выражения, стоящие в скобках, опять-таки положительны. Поэтому, по теореме о пределе монотонно возрастающей последовательности, существует конечный .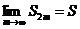

Рассмотрим теперь частные суммы знакопеременного ряда с нечетным индексом.Имеем

.

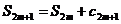Но тогда

.

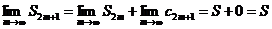Поэтому вообще 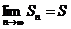и ряд 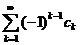сходится. <