Перестановки без повторений (см. 3.1) .
Размещение без повторенийиз 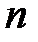 элементов по
элементов по 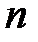 элементов называется перестановкой из
элементов называется перестановкой из 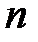 элементов.
элементов.
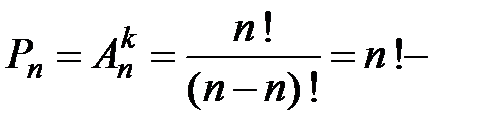 число всех перестановок из
число всех перестановок из 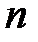 элементов.
элементов.
Пример 3.3. Пусть 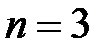 и в урне лежат три буквы
и в урне лежат три буквы 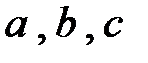 . Найти
. Найти 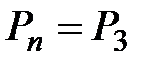 .
.
Решение.
1)Нахождение 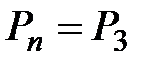 с помощью явного указания всех перестановок из трех элементов:
с помощью явного указания всех перестановок из трех элементов:
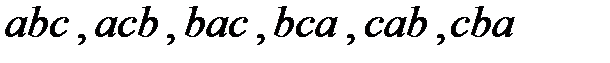 ;
; 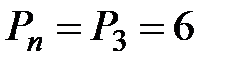 .
.
2) 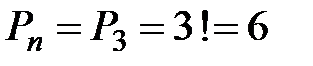 .
.
Можно показать, что все перестановки можно получить так:
а) выбираем одну (любую) перестановку;
б) переставляем всеми способами буквы в избранной перестановке.
Перестановки с повторениями.
Предположим, что имеется 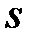 разных букв
разных букв 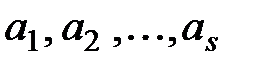 и в урне лежат следующие объекты:
и в урне лежат следующие объекты: 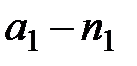 штук,
штук, 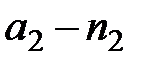 штук, …
штук, … 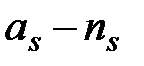 штук.
штук.
Из этой урны с возвращением вытаскиваем последовательно все 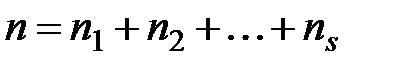 букв. Получается слово длины
букв. Получается слово длины 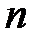 , если буква, появившаяся при вытаскивании с номером
, если буква, появившаяся при вытаскивании с номером 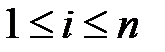 , вставляется в это слово на место с таким же номером
, вставляется в это слово на место с таким же номером 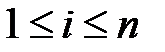 . Полученное слово называется перестановкой с повторениями и параметрами
. Полученное слово называется перестановкой с повторениями и параметрами 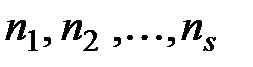 .
.
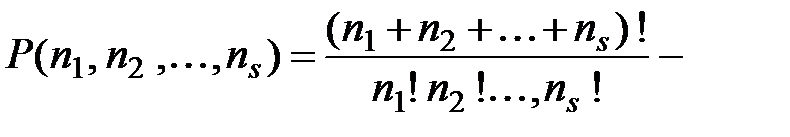 число всех разных перестановок с повторениями и параметрами
число всех разных перестановок с повторениями и параметрами 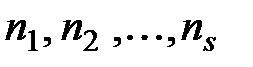 .
.
Пример 3.4. Пусть в урне лежат две буквы 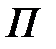 и две буквы
и две буквы 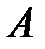 . Найти
. Найти 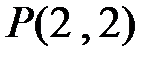 .
.
Решение.
1)Нахождение 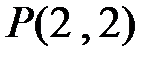 с помощью явного указания всех перестановок с повторениями и параметрами
с помощью явного указания всех перестановок с повторениями и параметрами 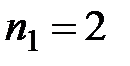 ,
, 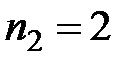 :
:
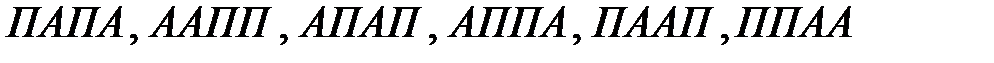 ;
; 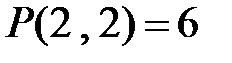 .
.
2) 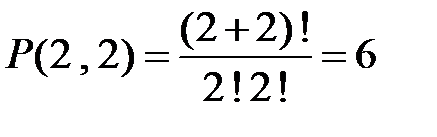 .
.
Доказательство формулы из 3.2.
Пусть 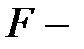 множество всех букв, лежащих в урне, а
множество всех букв, лежащих в урне, а 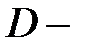 множество всех размещений с повторениями из
множество всех размещений с повторениями из 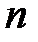 элементов по
элементов по 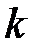 элементов. Ясно, что
элементов. Ясно, что 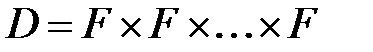 (всего
(всего 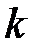 множителей). По правилу произведения
множителей). По правилу произведения 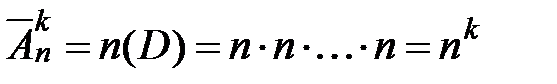 .
.
Сочетания без повторений. Треугольник Паскаля. Бином Ньютона.
Сочетания без повторений.
Рассмотрим конечное непустое множество 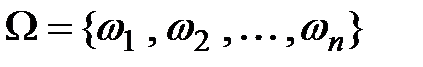 , где
, где 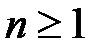 . Ясно, что
. Ясно, что 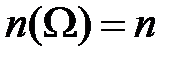 . Пусть
. Пусть 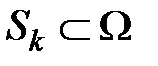 и
и 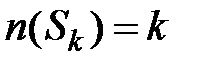 ,
, 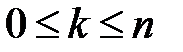 . Подмножество
. Подмножество 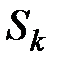 множества
множества  называется сочетанием без повторений из
называется сочетанием без повторений из 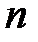 элементов по
элементов по 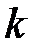 элементов.
элементов.
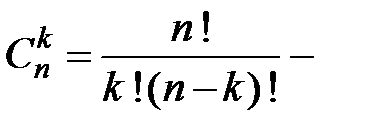 число всех сочетаний без повторений из
число всех сочетаний без повторений из 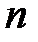 элементов по
элементов по 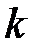 элементов.
элементов.
Если 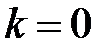 , то получается одно подмножество
, то получается одно подмножество 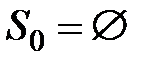 и
и 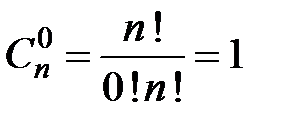 .
.
Пример 4.1. Пусть 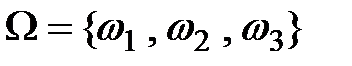 и
и 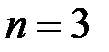 . Найти
. Найти 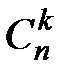 ,
, 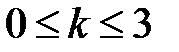 .
.
Решение.
Множество сочетаний и их количество выглядят так: 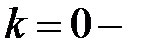
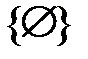 ,
, 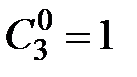 ;
;
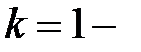
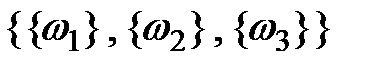 ,
, 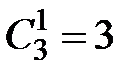 ;
; 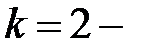
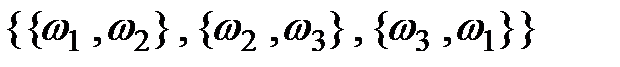 ,
, 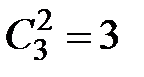 ;
; 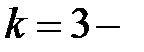
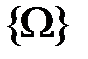 ,
, 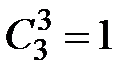 .
.
Треугольник Паскаля.
Свойство 4.1.Верны утверждения:
1) 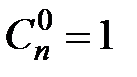 ,если
,если 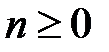 ; 2)
; 2) 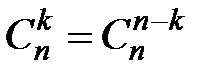 , если
, если 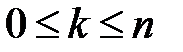 ;
;
3) 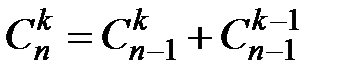 , если
, если 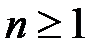 и
и 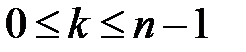 .
.
Свойство 4.1. позволяет построить бесконечный треугольник, который называется треугольником Паскаля. Он выглядит так:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
……………………………………….
В треугольнике Паскаля в строке с номером 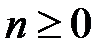 находятся числа
находятся числа 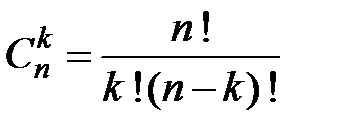 , где
, где 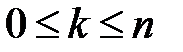 . В частности, в третьей строке:
. В частности, в третьей строке:
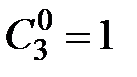 ,
, 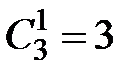 ,
, 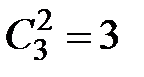 ,
, 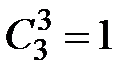 .
.
Каждое внутреннее число строки, начиная со второйстроки, равно сумме двух ближайших чисел из предыдущей строки (см. третье утверждение свойства 4.1). Каждое крайнее число строкиравно единице (см. первое равенство из первого утверждения свойства 4.1).
Бином Ньютона.
Свойство 4.2.Верны утверждения:
1) 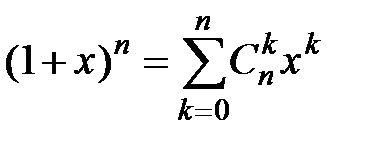 , где
, где 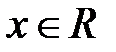 ,
, 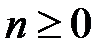 ,
, 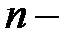 целое число;
целое число;
2) 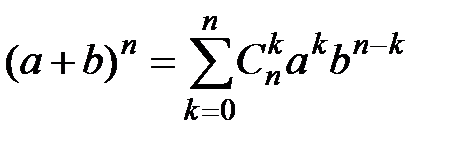 , где
, где 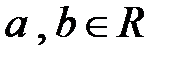 ,
, 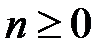 ,
, 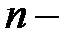 целое число;
целое число;
§5. Классическая вероятностная схема. Основные свойства вероятности события. Прикладные задачи. Элементарные события как возможные исходы некоторого испытания (опыта).
5.1. Основные определения. Вероятность события и ее свойства.
Рассмотрим конечное непустое множество 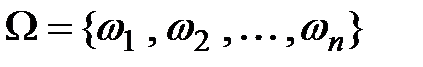 , где
, где 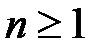 . Его элементы будем называть элементарными событиями, а само множество
. Его элементы будем называть элементарными событиями, а само множество 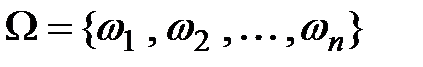 будем называть пространством элементарных событий.
будем называть пространством элементарных событий.
Определение. Любое подмножество множества 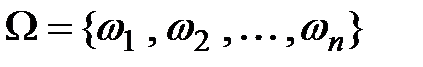 называется событием.
называется событием.
Другими словами, множество 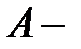 событие
событие 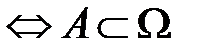 .
.
Так как 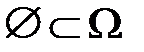 , то пустое множество является событием и называется невозможным событием.
, то пустое множество является событием и называется невозможным событием.
Так как 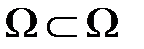 , то пространство элементарных событий является событием и называется достоверным событием.
, то пространство элементарных событий является событием и называется достоверным событием.
Ввиду того, что 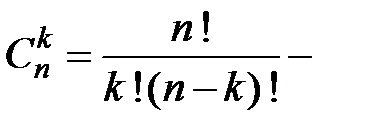 число событий, состоящих из
число событий, состоящих из 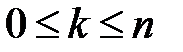 элементарных событий, то число всех событий в силу формулы бинома Ньютона равно
элементарных событий, то число всех событий в силу формулы бинома Ньютона равно
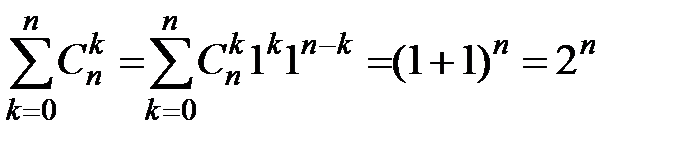 .
.
Видно, что все изучаемые нами события (специальные множества, состоящие из элементарных событий) содержатся в одном универсальном множестве  . При таких условиях можно применять пять основных операций над событиями, при этом используется следующая терминология: если
. При таких условиях можно применять пять основных операций над событиями, при этом используется следующая терминология: если 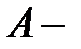 событие, то событие
событие, то событие 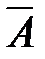 называется противоположным к событию
называется противоположным к событию 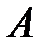 ; если
; если 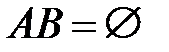 , то говорят, что события
, то говорят, что события 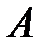 и
и 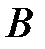 несовместны.
несовместны.
Определение. Для любого события 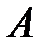 число
число
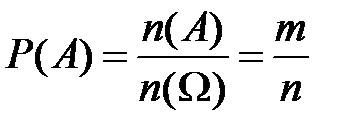 (5.1)
(5.1)
называется вероятностью события 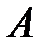 (вероятностной мерой события
(вероятностной мерой события 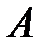 ).
).
Рассмотрим основные свойства вероятности 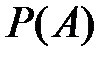 события
события 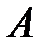 , опираясь на свойства другой меры
, опираясь на свойства другой меры 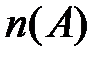 события
события 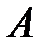 (числа элементов события
(числа элементов события 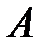 ).
).
Свойство 5.1. 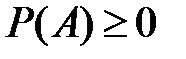 для любого события
для любого события 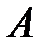 .
.
Свойство 5.2(вероятность достоверного события). 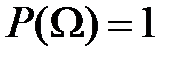 .
.
Свойство 5.3(теорема сложения или свойство конечной аддитивности вероятности 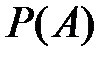 ). Верны утверждения:
). Верны утверждения:
1)если 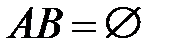 , то
, то 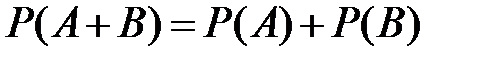 ;
;
2)если 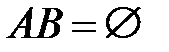 ,
, 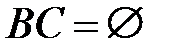 и
и 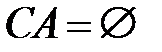 , то
, то 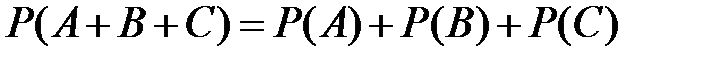 ;
;
3)если 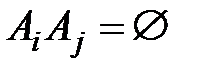 ,
, 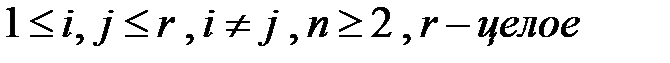 ,
,
то 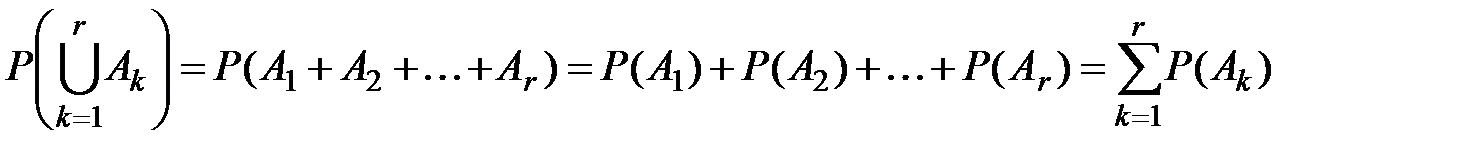 .
.
Замечание. Интересно, что свойства 5.4 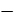 5.9 можно вывести из свойств 5.1
5.9 можно вывести из свойств 5.1 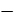 5.3. Если вместо формулы (5.1) вероятность вводится по-другому, то она тоже должна удовлетворять свойствам 5.1
5.3. Если вместо формулы (5.1) вероятность вводится по-другому, то она тоже должна удовлетворять свойствам 5.1 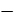 5.3, а значит и свойствам 5.4
5.3, а значит и свойствам 5.4 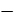 5.9 .
5.9 .
Поэтому свойства 5.1 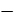 5.3 обычно объявляют аксиомами теории вероятностей, причем требуют, чтобы третье утверждение свойства 3 выполнялось и при
5.3 обычно объявляют аксиомами теории вероятностей, причем требуют, чтобы третье утверждение свойства 3 выполнялось и при 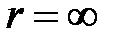 .
.
Если не удается ввести вероятность события для всех событий, то ее вводят для избранных событий (см. [6]).
Свойство 5.4(вероятность объединения).
Верны утверждения:
1) 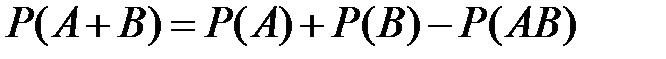 ;
;
2) 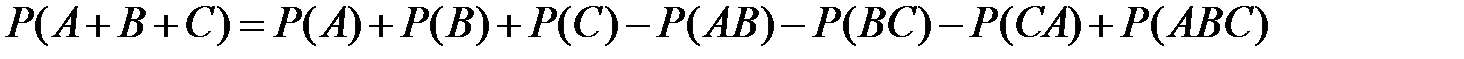 .
.
Свойство 5.5(вероятность разности).
Верны утверждения:
1) 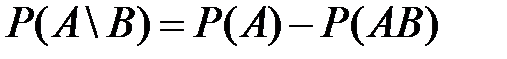 ;
;
2) 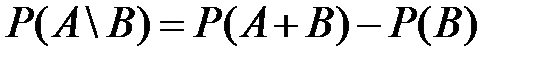 ;
;
3) если 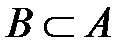 , то
, то 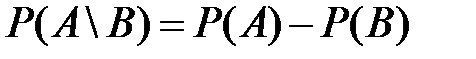 .
.
Свойство 5.6 (свойство монотонности вероятности 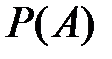 ).
).
Верны утверждения:
1)если 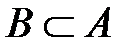 , то
, то 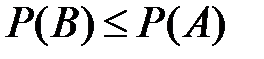 ;
;
2) 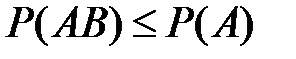 ,
, 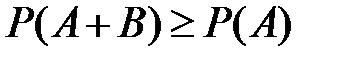 ;
;
3) 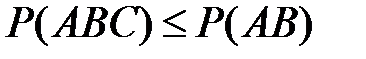 ,
, 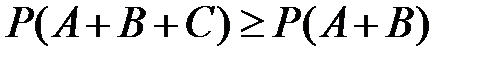
Свойство 5.7(вероятность противоположного события).
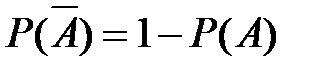 .
.
Свойство 5.8(вероятность невозможного события). 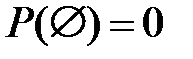 .
.
Свойство 5.9. 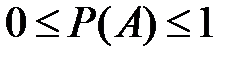 для любого события
для любого события 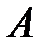 .
.
Свойство 5.10(о вероятностях элементарных событий).
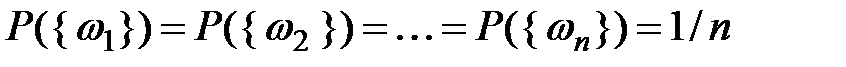 , т.е. вероятности всех элементарных событий равны.
, т.е. вероятности всех элементарных событий равны.
5.2. Прикладные задачи. Элементарные события как возможные исходы некоторого испытания (опыта).
Проводится некоторое испытание (опыт) с конечным числом возможных исходов 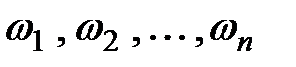 и это испытание может повторяться любое число раз. Если в результате испытания возникает некоторый возможный исход
и это испытание может повторяться любое число раз. Если в результате испытания возникает некоторый возможный исход 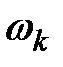 ,
, 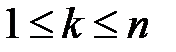 , то говорят, что он появляется или наступает. Предполагается, что выполнены следующие условия:
, то говорят, что он появляется или наступает. Предполагается, что выполнены следующие условия:
а) обязательно хотя бы один из возможных исходов 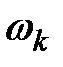 ,
, 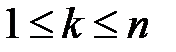 , наступит;
, наступит;
б) возможные исходы 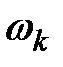 ,
, 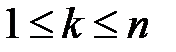 , с разными номерами одновременно наступить не могут;
, с разными номерами одновременно наступить не могут;
в) возможные исходы 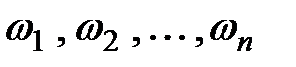 имеют одинаковые шансы появиться, т.е. нет оснований предполагать, что одни из них появляются чаще, чем другие.
имеют одинаковые шансы появиться, т.е. нет оснований предполагать, что одни из них появляются чаще, чем другие.
Последнее условие необходимо в силу свойства 5.10, которое было выведено из формулы (5.1). Если вероятность события вводится по другой формуле, то это условие надо поменять на другое. В прикладных задачах при их формулировке часто для соблюдения условия в) применяют следующие слова: «наугад», «симметричный», «одинаковый» и др.
После таких предположений можно говорить о множестве всех возможных исходов 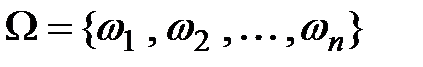 и следовать традиционной интерпретации терминов из предыдущей теории:
и следовать традиционной интерпретации терминов из предыдущей теории:
1)элементарные события отождествляются с возможными исходами;
2) событие 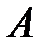 наступает (появляется), если наступает (появляется) элементарное событие в него входящее;
наступает (появляется), если наступает (появляется) элементарное событие в него входящее;
3) если элементарное событие есть элемент события 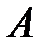 (входит в событие
(входит в событие 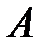 ), то говорят, что это элементарное событие благоприятствует событию
), то говорят, что это элементарное событие благоприятствует событию 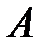 .
.
4)достоверное событие  наступает всегда, так как состоит из всех элементарных событий;
наступает всегда, так как состоит из всех элементарных событий;
5) невозможное событие  никогда не наступает, так как в нем нет элементарных событий;
никогда не наступает, так как в нем нет элементарных событий;
6)  тогда и только тогда, когда верно утверждение: если наступает событие
тогда и только тогда, когда верно утверждение: если наступает событие 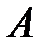 , то наступает событие
, то наступает событие 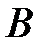 ;
;
7) событие 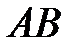 наступает тогда и только тогда, когда события
наступает тогда и только тогда, когда события 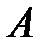 и
и 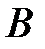 наступают одновременно;
наступают одновременно;
8) событие 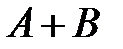 наступает тогда и только тогда, когда хотя бы одно из событий
наступает тогда и только тогда, когда хотя бы одно из событий 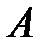 или
или 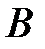 наступает;
наступает;
9) событие 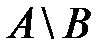 наступает тогда и только тогда, когда события
наступает тогда и только тогда, когда события 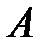 и
и 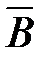 наступают одновременно;
наступают одновременно;
10) если наступает событие 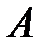 , то событие
, то событие 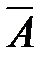 не наступает;
не наступает;
11)вероятность 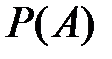 события
события 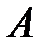 это оценка шансов наступления события
это оценка шансов наступления события 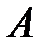 .
.
Пример 5.1. Симметричный игральный кубик наугад бросается один раз на гладкий стол. Найти вероятность того, что на верхней грани появится число, делящееся на три.
Решение.
Испытание 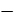 это однократное бросание кубика на гладкий стол наугад.
это однократное бросание кубика на гладкий стол наугад.
Шесть возможных исходов:
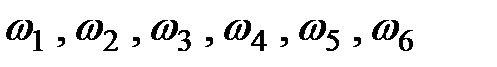 ;
;
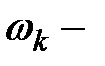 на верхней грани появился целый номер
на верхней грани появился целый номер 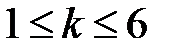 .
.
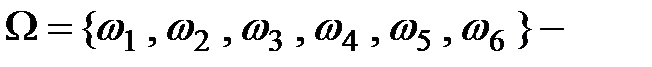 пространство элементарных событий.
пространство элементарных событий.
Событие 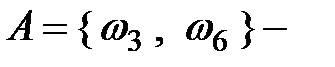 на верхней грани появится число, делящееся на три. В силу формулы (5.1) искомая вероятность равна
на верхней грани появится число, делящееся на три. В силу формулы (5.1) искомая вероятность равна
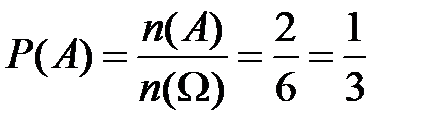 .
.
