Леонардо да Винчи. Пропорциональный канон

Многовековой опыт искусства, в котором прочно утвердились такие категории, как «целостность», «единство», «гармонич­ность», может быть перенесен и на характеристики произведений, о которых мы говорим: целостное произведение, композиционное единство, гармоничная композиция. Законы, по которым создают­ся такого рода произведения искусства, принято называть закона­ми гармонии. К ним относятся закон равновесия, закон единства и соподчинения. Однако и без художественных средств, помогаю­щих создавать композиции по законам гармонии, не обойтись. К их числу, как вы уже знаете, относятся ритм, контраст, нюанс, тожде­ство, а также пропорции и масштаб. Это основные средства гармо­низации. Композиций, созданных без их участия, просто не суще­ствует. Напомним, что во времена Гомера гармониями называли скрепы, соединяющие доски в обшивке корабля. Лишенный гармо­ний корабль распадался на отдельные доски.

Обратим внимание на одно из важнейших средств гармониза­ции — пропорции (связи частей и целого). Продолжая тему единст­ва целостного произведения, мы утверждаем, что пропорции и есть именно то средство, в основе которого заложена идея соотношения целого и составляющих это целое частей. Под пропорцией понима­ется отношение частей целого между собой и этим целым.

В эпоху Ренессанса среднепропорциональное отношение называ­ли Божественной пропорцией. Леонардо да Винчи, занимаясь систе­мами пропорционирования, дает ей название «золотое сечение».

Построим отрезки в пропорциях золотого сечения. В прямо­угольнике с соотношением сторон 1:2 проводится диагональ, на ко­торую поворотом накладывается меньшая сторона. Остаток диаго­нали поворачивается вокруг вершины прямоугольника до совме­щения с положением верхнего основания. Таким образом, верхнее основание поделилось на два неравных отрезка в пропорции золо­того сечения.

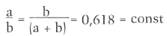Если с = 1, то b = 0,618, а = 0,382; если b = 1, то с = 1,618, а = 0,618; если а = 1, то b = 1,618, с = 2,618.

___________________________________________________________ СРЕДСТВА ГАРМОНИЗАЦИИ КОМПОЗИЦИИ

Вот как древние ученые понимали пропорцию: «Две части или две величины не могут быть связаны между собой без посредства третьей... Достигается это... пропорцией (аналогией), в которой из трех чисел... среднее так относится ко второму как первое к сред­нему а также второе к среднему как среднее к первому».

Стоит отметить особую роль среднего пропорционального. Оно содержит в себе качественное обобщение, так как выражается од­ним числом, а не множеством. Вот почему пропорции так сущест­венны в выражении гармонии.

Основные пропорции:

СРЕДСТВА ГАРМОНИЗАЦИИ КОМПОЗИЦИИ_________________________________________________________

Свойство аддитивности линейного ряда золотого сечения состо­ит в том, что каждый отрезок равен сумме или разности двух смежных отрезков.

С открытием в 1202 году ряда Фибоначчи было обнаружено основ­ное свойство золотого сечения — единство аддитивности и мультика-тивности. Это и есть суть золотого сечения. В нем ключ к явлению формообразования, открыто лежащий на поверхности математиче­ского знания. Но чтобы увидеть эту особенность, потребовалось сна­чала обнаружить механизм формообразования индуктивным путем.

В математике понятие «аддитивность» означает, что в числовом ряду Ф₁, Ф₂, Ф₃, Ф₄... Ф_n -₁, Ф_n каждый последующий член равен сум­ме двух предыдущих. Причем за начало такого ряда можно при­нять любые два числа, например 0 и 1, 1 и 3 или 1 и 4 и т. д.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610...

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207... 1, 4, 5, 9, 14, 23, 37, 60, 97, 157, 254, 411, 665, 1076, 1741, 2817... Мультипликативность означает, что в числовом ряду Ф₁₇ Ф₂, Ф₃,

Ф₄-.. Фп-1, Ф_п все члены ряда связаны в геометрическую прогрессию: Ф, ; ф₂ = ф₂: ф₃ = ф₃ : Ф₄ =...= Ф_n - ₁ : Ф_n = const.

Число золотого сечения, соединяющее свойства аддитивности и мультипликативности, находится как общий корень двух уравнений:

а + b = с (аддитивность)

а:b = b:с (мультипликативность),

в которых целое «с» представлено состоящим из двух час­тей а + б. Отношение золотого сечения — широко распространенная закономерность организации живой природы, которая за единством аддитивности и мультипликативности скрывает глобальный прин­цип построения мироздания.

Понятие аддитивности свидетельствует о том, что целое струк­турно... Понятие мультипликативности означает, что на все части структурно организованного целого распространяется одна и та же закономерность роста.

Например, в природе золотое сечение распространено очень ши­роко — как числовая характеристика членения стеблей растений, их расположения на стволе, закручивания спиралей подсолнечни­ка, описание пропорций человеческого тела, строения раковины, яйца, яблока и т. д.

__________________________________________________________ СРЕДСТВА ГАРМОНИЗАЦИИ КОМПОЗИЦИИ

Певучесть скрипки, красота ее голоса находится в прямой зави­симости от того, в какой мере форма инструмента согласована с пропорцией золотого сечения. Анализ музыкальных произведений в диапазоне от Баха до Шостаковича продемонстрировал метриче­ские отношения основных разделов музыкальных форм, а также золотое сечение. Таким образом, законы гармонии обнаружены в музыкальных рядах, в таблице Менделеева, в расстояниях между планетами, в микро- и макрокосмосе, во многих областях науки. Скульптура, архитектура, астрономия, биология, техника, психоло­гия и т. д. — везде так или иначе проявляет себя золотое сечение.

Обратимся к истории. Теперь нам точно известно, что автор одиннадцати деревянных досок — панелей из склепа древнеегипет­ского зодчего Хеси-Ра (XVIII в. до н. э., Древнее царство) — вирту­озно применял не только законы золотого сечения, но и был зна­ком с общекосмическим феноменом гармонии. Он также проил­люстрировал правило золотого сечения во всевозможных вариаци­ях и дал практические советы по его использованию в творчестве.

Сегодня невозможно с абсолютной достоверностью определить, когда и как понятие золотого сечения было выделено человеком из интуитивной и опытной категории.

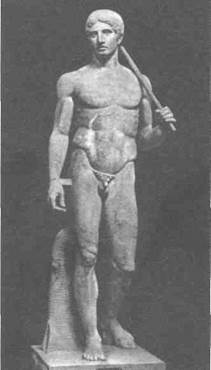
Рассмотрим скульптуру Поликлета «Дорифор», вплоть до мель­чайших деталей построенную в пропорции золотого сечения. Канон Поликлета был известен еще в Древнем Египте. Именно там его по­знал Пифагор, а затем передал свои знания ученикам. Как известно, Поликлет был выходцем из школы Пифагора. Судя по всему, Поликлет не был посвящен во все таинства канона. Приняв систему чле­нения только как описывающую физические, внешние данные че­ловека, он допустил ошибку. В результате голова его скульптур не­сколько массивна, тяжеловесна. Позднее Лисипп пересмотрел огра­ничения канона и более творчески подошел к нему.

Из всего ряда древних канонов, включая современный канон Ле Корбюзье, только канон древних египтян носит абстрактный харак­тер: в нем нет человеческого изображения. Однако в нем закодиро­ваны ритмы мужского и женского тела. Поисками канона, дающего гармонию, занимались многие художники, скульпторы, архитекто­ры. Они создавали так называемые «модулёры», в основу которых были заложены найденные ими системы пропорционирования.