Эллиптические параболоиды

Поверхности второго порядка

Поверхность вращения и преобразование сжатия

Поверхность вращения. Простейшие поверхности в пространстве – это плоскости. Они являются геометрическими образами уравнений первой степени от трех переменных. Другой достаточно простой тип поверхностей составляют поверхности вращения.

Определение. Поверхность 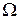называют поверхностью вращения, если она образована окружностями с центрами на некоторой прямой 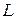(оси вращения), которые расположены в плоскостях, перпендикулярных .

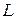Уравнение поверхности вращения 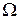имеет наиболее простой вид, когда начало 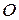прямоугольной системы координат лежит на оси вращения, а ось 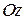совпадает с ней. Пересечение поверхности 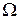с координатной плоскостью 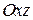– это некоторое множество 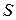, вращение которого образует .

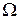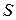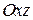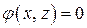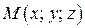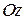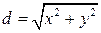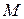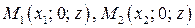Предположим, что множество в плоскости описывается уравнением . Рассмотрим произвольную точку . Она удалена от оси на расстояние . Если точка лежит на поверхности вращения , то точки с той же аппликатой 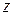, что и 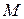, и абсциссами 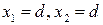принадлежат множеству . Поэтому

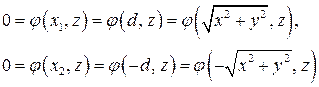
и условие 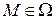сводится к тому, что координаты точки 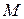удовлетворяют равенству

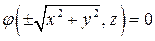. (1)

Уравнение (1) и есть уравнение поверхности 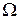, которая образована вращением подмножества 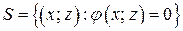, расположенного в координатной плоскости 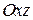. Из уравнения множества 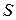уравнение (1) соответствующей поверхности вращения получается заменой 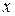на .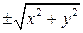

Преобразование сжатия. Под преобразованием сжатия к координатной плоскости 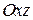мы понимаем такое преобразование, при котором точка 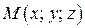смещается в точку 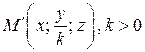. Параметр 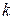называют коэффициентом сжатия. При 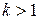точки пространства, расположенные на одной прямой, перпендикулярной плоскости 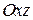, в результате такого преобразования сближаются, т.е. преобразование – действительно сжатие. При 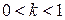преобразование фактически является растяжением.

Пусть в пространстве в прямоугольной системе координат 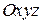некоторое множество 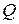задано своим уравнением 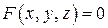. При преобразовании сжатия к координатной плоскости 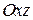с коэффициентом 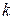это множество превратится в новое множество 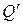с уравнением 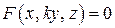. Это следует из того, что точка 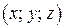тогда и только тогда принадлежит множеству 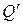, когда точка 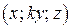принадлежит множеству .

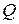Эллипсоиды

Поверхность, которая получается при вращении эллипса вокруг одной из его осей симметрии, называют эллипсоидом вращения.

Уравнение эллипсоида выведем, расположив начало прямоугольной системы координат в центре эллипса и совместив ось аппликат 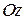с осью вращения, а координатную плоскость – с плоскостью эллипса. Тогда уравнение эллипса будет иметь вид

.

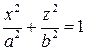Если в этом уравнении заменить 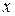на 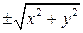, то получится уравнение

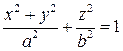
соответствующей поверхности вращения. Итак, эллипсоид с осью вращения 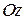описывается уравнением

.

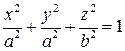Применим к эллипсоиду преобразование сжатия к координатной плоскости 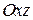, получим эллипсоид общего вида. Если 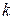– коэффициент сжатия, то уравнение эллипсоида будет иметь вид

,

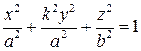или, после переобозначения параметров,

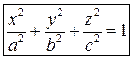. (2)

Уравнение (2) задает поверхность второго порядка. Его называют каноническим уравнением эллипсоида. Три параметра 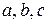, входящие в него – это полуоси эллипсоида.

Если равны все три полуоси 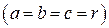, то эллипсоид превращается в сферу радиуса 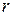, которая описывается уравнением

.

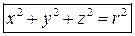Гиперболоиды

При вращении гиперболы вокруг одной из ее осей симметрии получается поверхность, называемая гиперболоидом вращения. Выбор оси вращения влияет на тип гиперболоида. Если осью вращения является действительная ось симметрии гиперболы, то поверхность будет состоять из двух частей (полостей). Это двуполостный гиперболоид вращения. При вращении гиперболы вокруг ее мнимой оси симметрии поверхность будет состоять из одной полости. Такую поверхность называют однополостным гиперболоидом вращения.

Для вывода уравнений гиперболоидов расположим прямоугольную систему координат так, чтобы ось вращения, являющаяся осью симметрии гиперболы, совпадала с осью аппликат 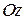, сама гипербола располагалась в координатной плоскости 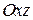с центром в начале системе координат.

Для случая двуполостного гиперболоида уравнение гиперболы будет иметь вид

.

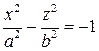Заменив в нем 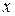на 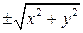, получим уравнение

.

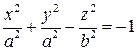В случае однополостного гиперболоида гипербола будет описываться уравнением

.

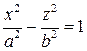Опять меняем 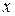на радикал 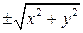, получаем уравнение

.

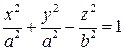Гиперболоиды преобразованием сжатия к координатной плоскости превращаются в двуполостный, однополостный гиперболоиды общего вида. При коэффициенте сжатия их уравнениями будут соответственно

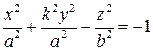и .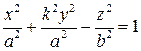

После переобозначений параметров эти уравнения преобразуются в каноническое уравнение двуполостного

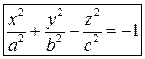
и однополостного гиперболоидов

.

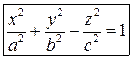Эллиптические параболоиды

При вращении параболы вокруг ее оси получаем параболоид вращения. Чтобы найти его уравнение, выберем прямоугольную систему координат, направив ось 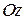по оси вращения и совместив координатную плоскость 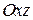с плоскостью параболы. Пусть при этом парабола описывается уравнением . Тога для получения уравнения поверхности вращения нужно заменить в этом уравнении 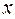на :

.

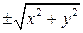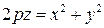Преобразование сжатия параболоида вращения к координатной плоскости 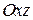с коэффициентом 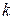дает поверхность более общего вида – эллиптический параболоид, уравнением которого будет

.

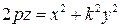После переобозначения параметров получаем каноническое уравнение эллиптического параболоида

.

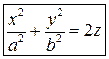Конусы

При вращении прямой 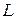, пересекающийся с осью вращения, образуется прямой круговой конус. Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса.

Уравнение будем выводить в прямоугольной системе координат, ось 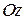которой совпадает с осью вращения, а начало системы координат – с вершиной конуса. Ось 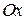расположим так, чтобы прямая 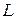находилась в координатной плоскости 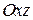и описывалась уравнением 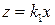. В этой системе координат уравнение поверхности вращения получается из уравнения прямой заменой 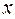на 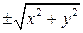. В результате такой замены получаем 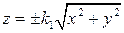. Возведя уравнение в квадрат, придем к соотношению 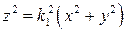, а разделив его на :

.

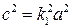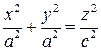Преобразование сжатия прямого кругового конуса к координатной плоскости 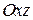с коэффициентом 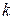дает эллиптический конус. Его уравнение имеет вид

,

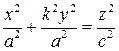или, после переобозначения параметров, получим каноническое уравнение прямого кругового конуса

.
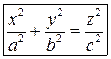