Спектры аналоговых и дискретных сигналов
Сигналы
1. Аналитическая запись дискретного сигнала
| а | 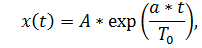 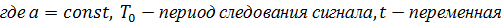 |
| б | 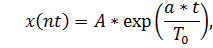 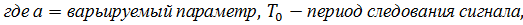 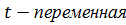 |
| в | 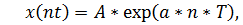 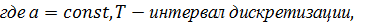 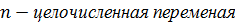 |
2. Дискретный сигнал квантованный по времени
| а | 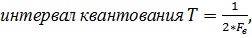 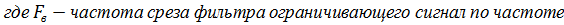 |
| б | 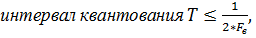 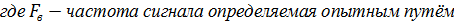 |
| в | 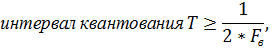 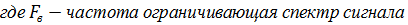 |
| г | 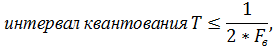 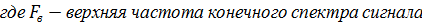 |
3. Примеры дискретных сигналов
| а | 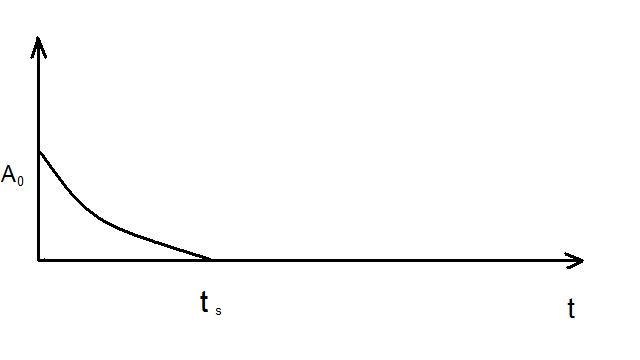 |
| б | 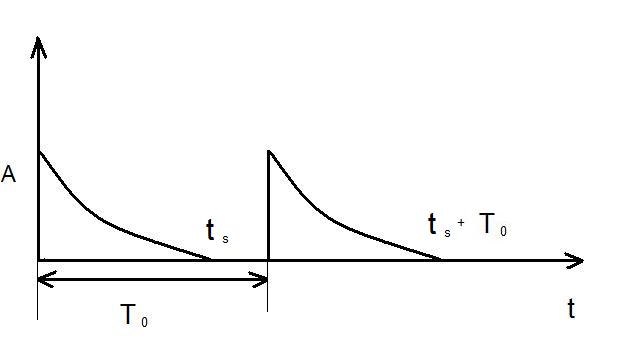 |
| в | 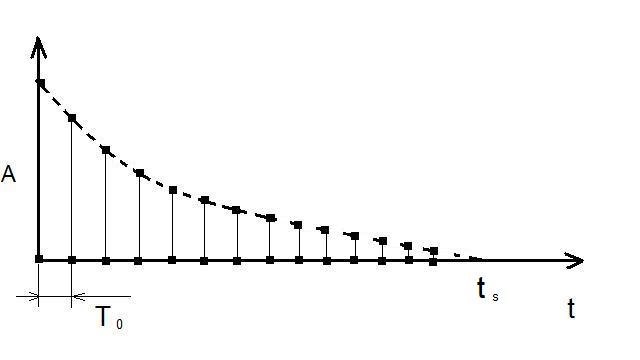 |
| г | 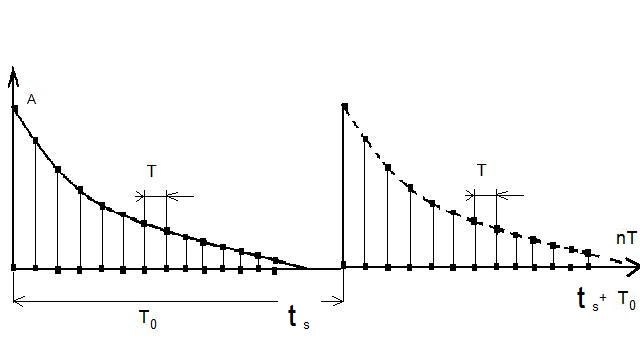 |
4. Аналитическая запись цифровых последовательностей
| а | 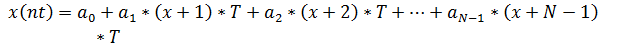 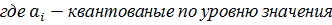 |
| б | 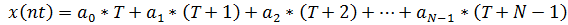 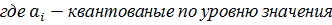 |
| в | 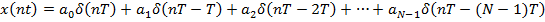 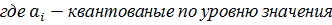 |
5. Периодическая последовательность и её особенности
| а | 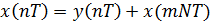 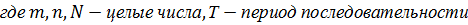 |
| б | 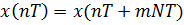 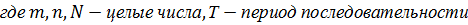 |
| в | 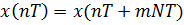 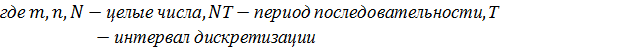 |
6. Сдвиг последовательности
Если последовательность x(nT)={1,2,3,0,0,0} с периодом N=6 сдвинуть вправо на 2 отсчёта то получим:
| а | x(nT)={1,2,0,0,0,3} |
| б | x(nT)={0,0,1,2,0,3} |
| в | x(nT)={0,0,1,2,3,0} |
| г | x(nT)={3,0,0,0,1,2} |
Дискретное преобразование Фурье
1. Для каких сигналов используется ДПФ:
| а | аналоговых |
| б | аналоговых периодических |
| в | дискретных периодических |
2. Прямое дискретное преобразование Фурье:
| а | 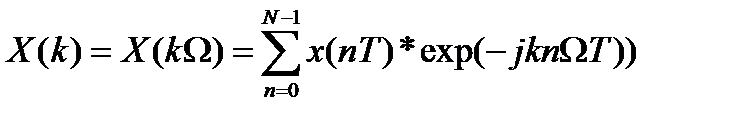 , где k=0, 1, 2, …N-1 , где k=0, 1, 2, …N-1 |
| б | 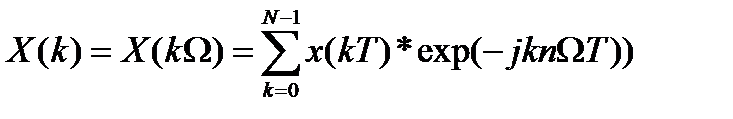 , где n=0, 1, 2, …N-1 , где n=0, 1, 2, …N-1 |
| в | 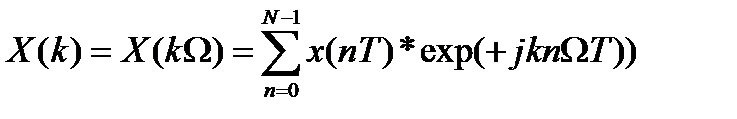 , где k=0, 1, 2, …N-1 , где k=0, 1, 2, …N-1 |
3. Обратное ДПФ:
| а | 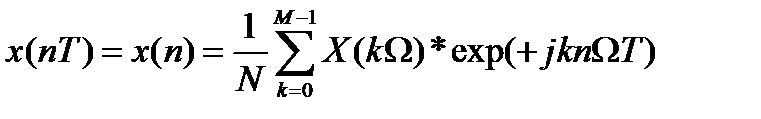 , где n=0, 1, 2, …N-1 , где n=0, 1, 2, …N-1 |
| б | 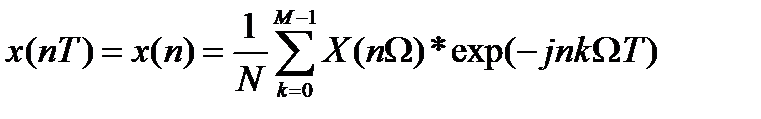 , где n=0, 1, 2, …N-1 , где n=0, 1, 2, …N-1 |
| в | 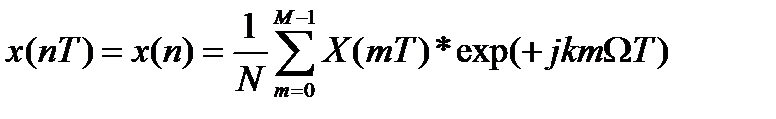 , где n=0, 1, 2, …N-1 , где n=0, 1, 2, …N-1 |
4. Использование ДПФ для получения свертки сигналов x1(nT) и x2(nT)
| а | для последовательности  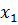 (nT) определить ДПФ (nT) определить ДПФ 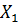 (k), для последовательности (k), для последовательности 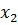 (nT) определить ДПФ (nT) определить ДПФ 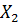 (k), затем перемножить (k), затем перемножить 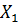 (k)* (k)* 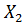 (k)=Y(k) и взять обратное ДПФ от Y(k) и получить y(nT) (k)=Y(k) и взять обратное ДПФ от Y(k) и получить y(nT) |
| б | последовательность 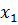 (nT) умножить на (nT) умножить на 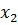 (nT), затем взять ДПФ от произведения (nT), затем взять ДПФ от произведения 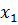 (nT)* (nT)* 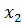 (nT), далее взять обратное ДПФ и получить свертку сигналов (nT), далее взять обратное ДПФ и получить свертку сигналов 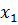 (nT) и (nT) и 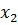 (nT) (nT) |
| в | для последовательности 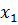 (nT) определить прямое ДПФ (nT) определить прямое ДПФ 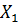 (k), умножить (k), умножить 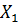 (k) на вторую последовательность (k) на вторую последовательность 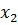 (nT), затем определить обратное ДПФ от полученного произведения и получить свертку сигналов (nT), затем определить обратное ДПФ от полученного произведения и получить свертку сигналов 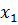 (nT) и (nT) и 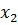 (nT) (nT) |
| г | для последовательности 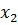 (nT) определить прямое ДПФ, затем умножить его на первую последовательность (nT) определить прямое ДПФ, затем умножить его на первую последовательность 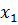 (nT), далее определить обратное ДПФ от произведения и получить свертку двух последовательностей (nT), далее определить обратное ДПФ от произведения и получить свертку двух последовательностей 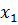 (nT) и (nT) и 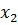 (nT) (nT) |
5. Какие Вы знаете алгоритмы вычисления ДПФ:
| а | Прореживание по времени и по частоте, при этом длина последовательности должна быть кратной 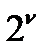 , где ν – целое число 1, 2, 3, … , где ν – целое число 1, 2, 3, … |
| б | Прореживание по времени и по частоте, длина последовательности может быть любой |
| в | Прореживание по времени и по частоте, длина последовательности должна быть четной 2ν , где ν – целое число 1, 2, 3, … |
| г | Прореживание по времени и по частоте, длина последовательности должна быть нечетной 2ν+1, где ν – целое число 1, 2, 3, … |
Спектры аналоговых и дискретных сигналов
1. Чем отличаются спектры аналоговых и дискретных сигналов?
| а | спектры аналоговых и дискретных сигналов одинаковы |
| б | спектр аналогового сигнала непрерывный, а дискретного – линейчатый |
| в | спектр аналогового сигнала линейчатый, а дискретного – непрерывный и периодический с частотой повторения fд |
| г | спектр аналогового сигнала существует в единственном числе на всей частотной оси, а спектр дискретного сигнала имеет такую же форму как аналоговый, но периодически повторяется с частотой дискретизации на всей частотной оси |
2. Что происходит с дискретным сигналом, если его спектр сдвигается на частоту f1?
| а | сигнал переместится по временной оси на время 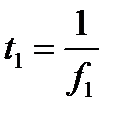 |
| б | останется без изменения |
| в | сигнал изменится путем умножения на дискретную экспоненту 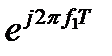 , то есть , то есть 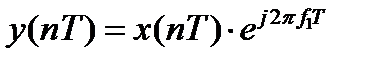 |
3. Что происходит со спектром сигнала, если сигнал переместить во времени вправо на величину 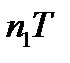 ?
?
| а | спектр переместиться также вправо на частоту 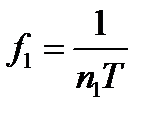 |
| б | АЧХ спектра останется без изменения, а частотная характеристика (ФЧХ) получит приращение 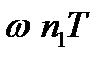 |
| в | спектр сигнала изменится путем умножения исходного спектра на дискретную экспоненту, то есть 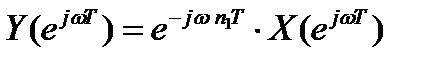 |
4. Каким образом связаны между собой аналоговый и дискретный сигналы и их спектры?
| а | согласно теореме отсчетов аналоговый сигнал может быть получен по отсчетам дискретного сигнала с помощью восстанавливающего ряда ортогональных функций вида sinc(x) |
| б | дискретный сигнал может быть получен из аналогового путем взятия отсчетов в дискретные моменты времени через интервалы времени, определяемые аппаратурными возможностями дискретизатора |
| в | спектр дискретного сигнала можно получить путем периодического повторения спектра аналогового сигнала через частотный интревал, равный частоте дискретизации |
5. Чему равна длина линейной свертки двух дискретных сигналов?
| а | длине сигнала с наименьшим числом отсчетов |
| б | длине сигнала с наибольшим числом отсчетов |
| в | длине, равной сумме длин входящих в свертку сигналов |
| г | длине, равной сумме длин без одного отсчета, входящих в свертку сигналов |
6. Чему равен период круговой свертки?
| а | если периоды сворачиваемых последовательностей одинаковы, то период круговой свертки будет равен периоду сворачиваемых последовательностей |
| б | если периоды сворачиваемых последовательностей одинаковы, то период круговой свертки будет равен сумме периодов сворачиваемых последовательностей |
| в | если периоды сворачиваемых последовательностей разные, то период круговой свертки будет равен сумме периодов сворачиваемых последовательностей |
| г | если периоды сворачиваемых последовательностей разные, то период круговой свертки будет равен наибольшему периоду из сворачиваемых последовательностей |
Дискретные системы
1. Аналитическое описание дискретных систем (линейное разностное уравнение)
| а | 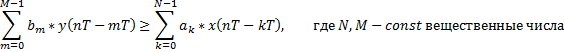 n=0,1,2,... n=0,1,2,... |
| б | 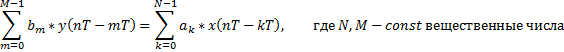 n=0,1,2,... n=0,1,2,... |
| в | 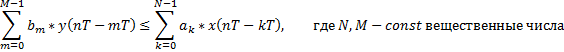 n=0,1,2,... n=0,1,2,... |
| г | 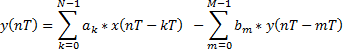 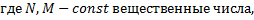 n=0,1,2,... n=0,1,2,... |
2. Прямое Z-преобразование
| а | 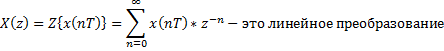 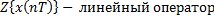 |
| б | 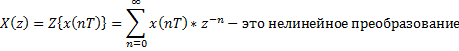 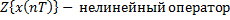 |
| в | 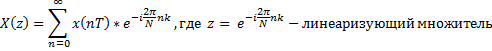 |
3. Обратное Z-преобразование
| а | 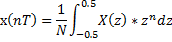 |
| б | 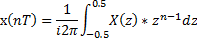 |
| в | 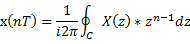 |
4. Передаточная функция дискретной системы
| а | 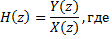 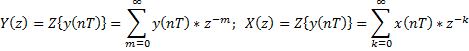 |
| б | 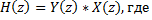 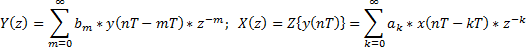 |
| в | 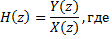 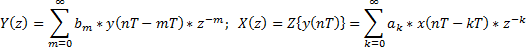 |
| г | 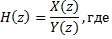 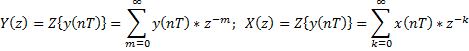 |
5. Структурные схемы дискретных систем
| 1 рекурсивная форма | а 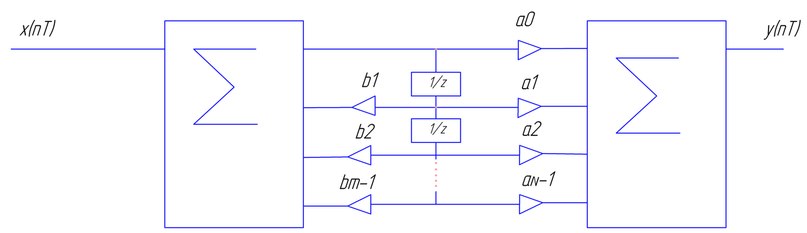 |
| 2 прямая рекурсивная форма | |
| 3 прямая трансверсальная форма | б 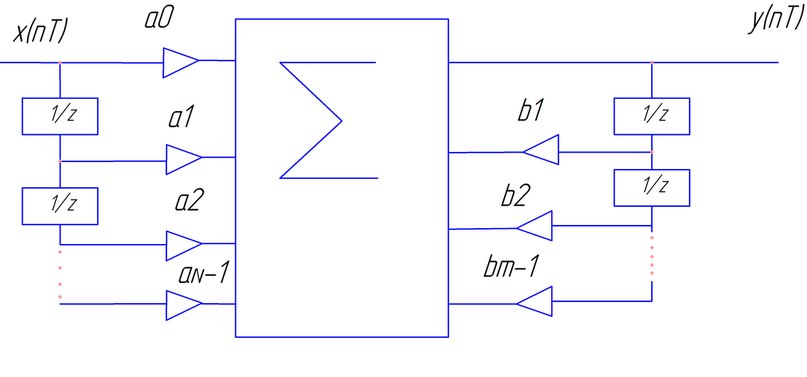 |
| 4 трансверсальная форма | |
| 5 каскадная трансверсальная форма | в 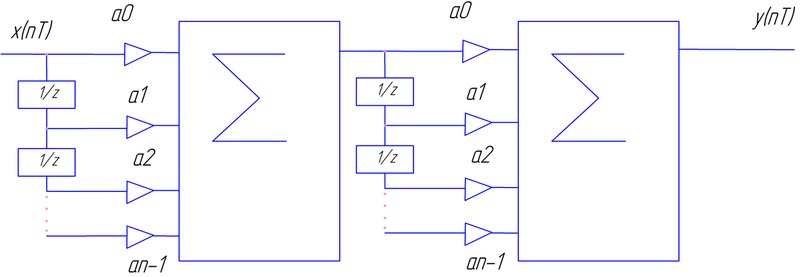 |
| 6 каскадная рекурсивная форма | |
| 7 прямая каноническая форма |
6. Критерий устойчивости дискретных систем
а 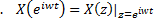 | д. полюсы и нули передаточной функции за пределами единичной окружности |
б. 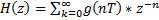 | е. полюсы и нули передаточной функции внутри единичной окружности |
в. 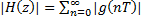 | ж. только нули передаточной функции внутри единичной окружности |
г. 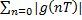 < ∞ < ∞ | з. только полюс передаточной функции внутри единичной окружности |
