Метод вспомогательных концентрических сфер

Метод вспомогательных секущих концентрических сфер можно применять только при наличии следующих условий:

1) пересекающиеся поверхности являются поверхностями вращения,

2) оси вращения этих поверхностей пересекаются,

3) пересекаясь, оси образуют плоскость, параллельную одной из плоскостей проекций.

Исходя из этого, решение задачи надо начинать с проверки выполнения всех этих условий.

Метод вспомогательных секущих концентрических сфер основан на том, что если поверхность вращения пересечь секущей сферой, центр которой лежит на оси вращения поверхности, то линия пересечения этих поверхностей есть окружность, центр которой лежит на оси вращения поверхности. Причем, эта окружность лежит в плоскости параллельной одной из плоскостей проекций, а следовательно, на нее проецируется в натуральную величину, а на другую плоскость проекций проецируется в прямую, соединяющую точки пересечения очерков поверхностей (рис.27).

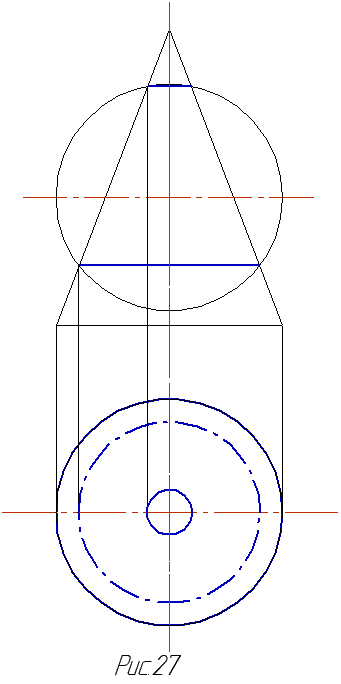
Если поверхности удовлетворяют вышеперечисленным требованиям, то решение начинают с выбора первой секущей сферы. Центр ее располагают в точке пересечения осей поверхностей. Радиус первой сферы подбирают таким образом, чтобы она касалась большей из поверхностей. Тогда линия касания является окружностью, а другую поверхность сфера пересечет по окружности. Точка пересечения этих окружностей и есть общая точка поверхностей (рис.28).

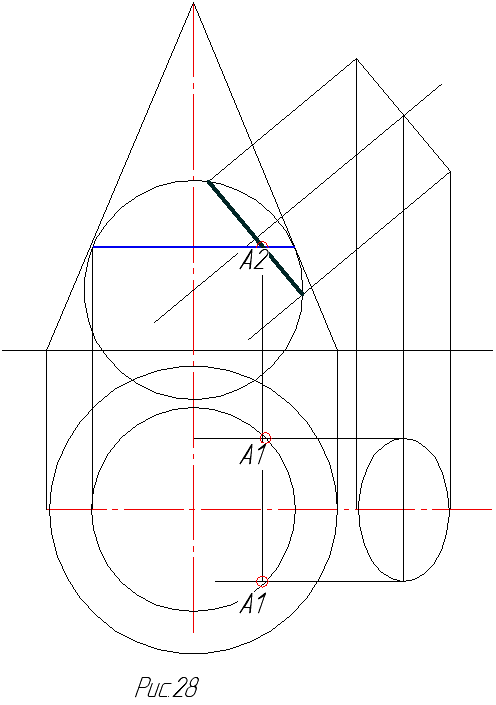
Постепенно увеличивая радиус сферы, находят точки пересечения окружностей, т.е. множество точек, принадлежащих линии пересечения поверхностей (рис.29).

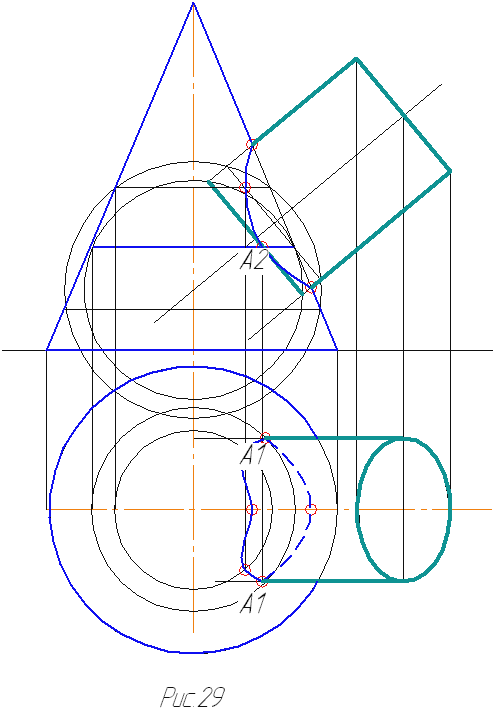
Заключение по первой части задания №4

Рассмотренные выше задачи должны продемонстрировать сложность решения задачи по построению линии пересечения поверхностей. Решение усложняется еще и тем, что для каждого варианта студентам предложены различные задачи и подобрать способ решения их довольно сложно. Отсюда совет - при выполнении задания №4 необходимо посоветоваться с преподавателем и только после этого приступать к решению задачи.

Построение разверток поверхностей

Вторая часть задачи №2 состоит из построения развертки одной из пересекающихся поверхностей с нанесением на ней точек линии пересечения. Выбор развертываемой поверхности зависит от желания студента. Но необходимо учесть, что не стоит разворачивать сферу или тор. Лучше развернуть гранную поверхность или цилиндр, или конус.

Развертка призмы

Развертка призмы представляет собой прямоугольник, высота которого равна высоте призмы, а длина равна периметру основания призмы. Если призма прямая, то построение развертки выполняется просто, т.к. на чертеже есть натуральная величина и основания призмы и ее высота (рис.30).

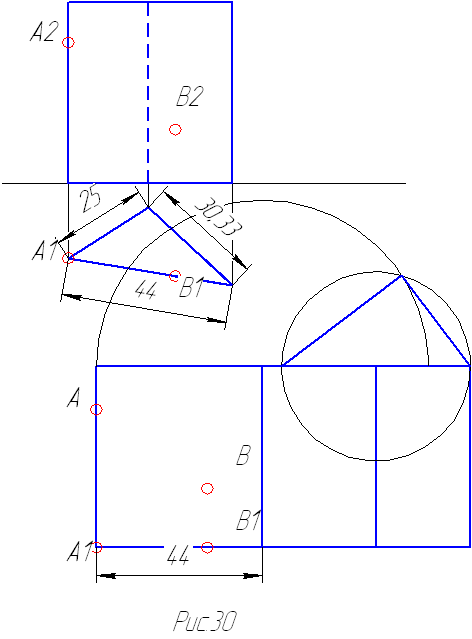
Развертка пирамиды

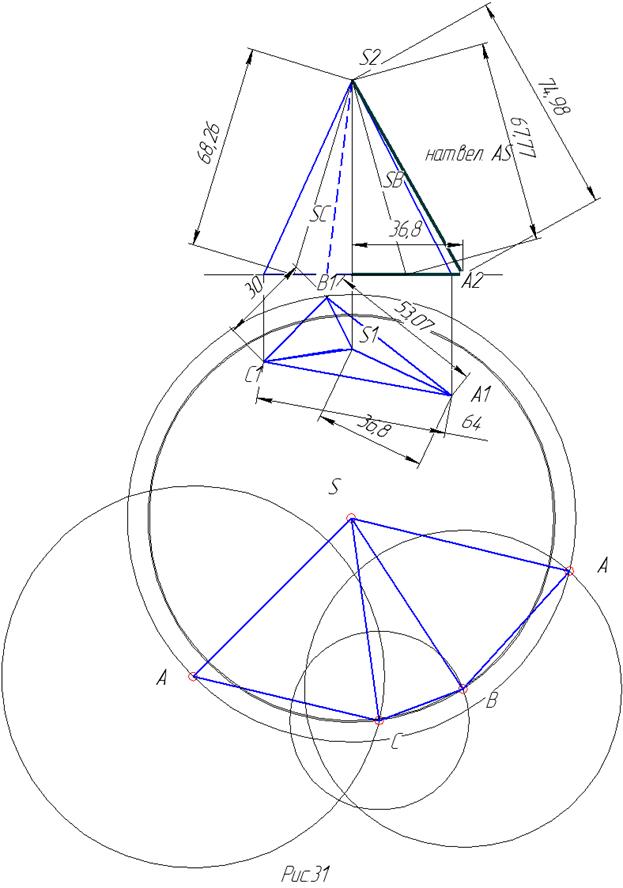
Чертеж пирамиды и построение ее развертки показаны на рисунке 31. Из чертежа видно, что натуральная величина основания пирамиды совпадает с горизонтальной проекцией основания пирамиды, а вот ребра пирамиды не проецируются на плоскости проекций в натуральную величину. Следовательно, для построения развертки надо построить сначала натуральную величину ребер пирамиды. Можно воспользоваться нахождением натуральной величины отрезка с помощью прямоугольного треугольника. Причем если рассматривать ребра пирамиды как отрезки, то для всех ребер пирамиды разница координат Z одинакова и равна высоте пирамиды. Поэтому, чтобы найти величину ребра пирамиды, достаточно отложить величину горизонтальной проекции ребра по оси Х , используя высоту пирамиды как катет прямоугольного треугольника, тогда гипотенуза этого треугольника и есть натуральная величина ребра.

Развертка пирамиды есть треугольники, являющиеся натуральной величиной боковых граней пирамиды и ее основания (рис.31).

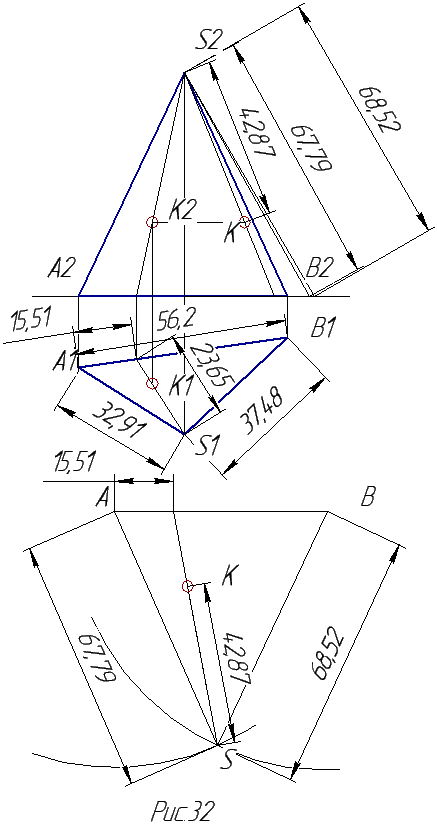
Точку на поверхности пирамиды надо искать из условия принадлежности точки плоскости. Следовательно, через точку надо провести прямую, лежащую в плоскости треугольника, построить ее на развертке и на ней найти саму точку (рис.32).Причем прямую надо проводить так, чтобы ее можно было просто построить на развертке, например, через вершину треугольника на основание.

.

Развертка цилиндра

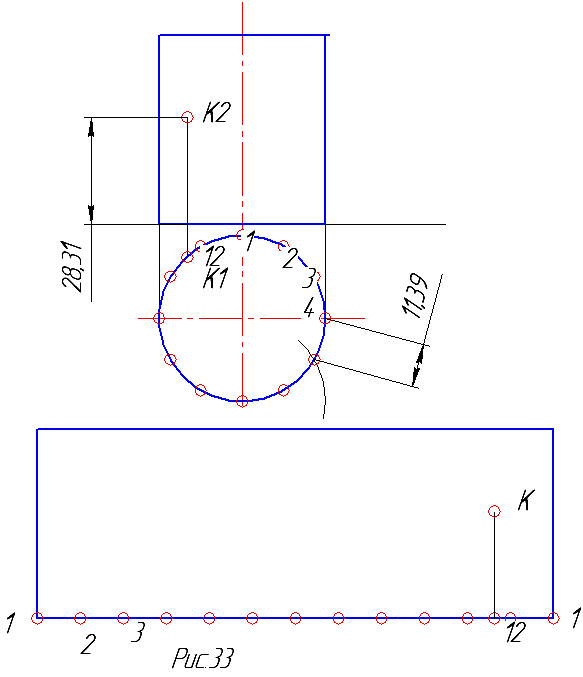
Развертка боковой поверхности цилиндра есть прямоугольник, высота которого есть высота цилиндра, а длина равна длине окружности основания цилиндра. Для того чтобы не считать длину окружности основания цилиндра и для упрощения нахождения в дальнейшем точек на поверхности, применим метод разбивки основания цилиндра на равное количество частей и чем больше это количество, тем точнее будет построение, т.к. длину дуги будем заменять длиной хорды, соединяющей концы дуги (рис.33).

Развертка конуса

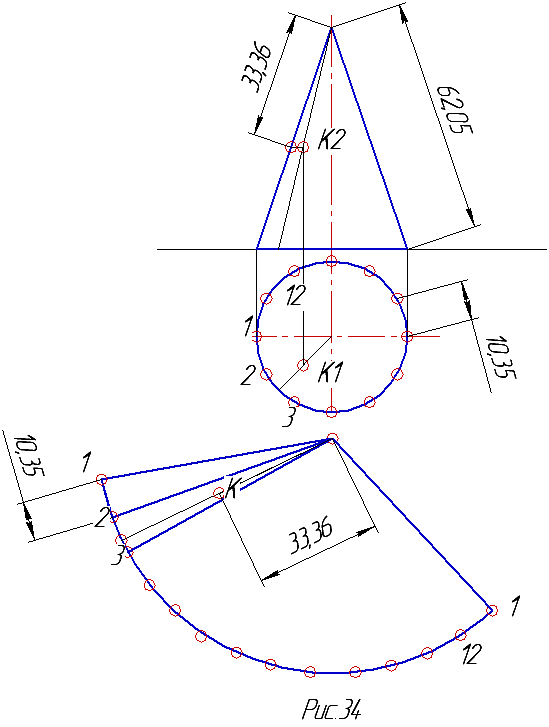
Развертка боковой поверхности конуса есть сектор круга, радиус которого равен натуральной величине образующей конуса. Угол этого конуса можно рассчитать по формуле, но это непрактично, т.к. при построении развертки подразумевается то, что надо будет искать точки на поверхности. Поэтому в качестве ограничения сектора лучше использовать крайние точки, лежащие на основании сектора, т.е. на дуге. Для этого надо разбить основание конуса на равные части аналогично построению развертки цилиндра и, заменяя длину дуги длиной хорды, отложить необходимое количество отрезков по дуге, радиус которой равен длине образующей конуса (рис.34). На этом же рисунке показано нахождение точки на поверхности конуса. Для нахождения точки надо через нее провести образующую. Найти основание образующей, найти на развертке это основание, через него провести образующую на развертке и на ней отложить расстояние от точки до вершины конуса. Причем это расстояние находят на чертеже. Для этого фронтальную проекцию точки переносят на очерковую образующую с помощью горизонтальной линии и тогда расстояние от точки до вершины конуса замеряют по очерковой образующей.

ЗАКЛЮЧЕНИЕ

В данном методическом пособии рассмотрены приемы решения задач по теме поверхности. Решение необходимо проводить сначала на черновике большого формата для выяснения того, как лучше расположить чертеж в чистовом варианте. Желательно, прежде чем оформлять решение, показать черновик преподавателю и только после этого проводить оформление.