Индикация ошибок при использовании формул

В случае неправильного использования функций Excel сообщает пользователю о допущенной ошибке. Перед сообщением об ошибке всегда присутствует знак # (диез). Смысл наиболее часто встречающихся сообщений приведен на рис. 3.25.

Сообщение	Ошибка
Последовательность знаков диез	Ширина ячейки недостаточна для размещения результата
#ССЫЛКА	В формуле задана ссылка на несуществующие ячейки
#ДЕЛ/0	Деление на нуль
#ЧИСЛО!	Нарушение правил работы с оператором, например, отрицательная величина под корнем
#ИМЯ?	Неправильно задано имя функции
#ПУСТО!	Неверно указаны диапазоны. Они не имеют общих ячеек
#Н/Д!	Ячейка–аргумент функции, не содержит данных
#ЗНАЧ!	Задан аргумент недопустимого типа

Рис.3.25Индикация ошибок при использовании формул

§10. Решение уравнений с одним неизвестным с использованием функций Excel 2010 (подбор параметра)

В экономической работе и других областях деятельности часто приходится сталкиваться с задачами по вычислению какого-либо параметра математического выражения. Рассмотрим несколько примеров.

Пример первый

Уровень инфляции 10% в год. Чему равен ежемесячный рост цен? Для определения увеличения цен за месяц необходимо решить уравнение (1+Х)¹²=1,10.

В ячейку А1 рабочего листа Excel вносим какое-либо число, которое, по нашему мнению, может быть решением, например 1. В другую ячейку, например В1 записываем формулу зависимости годовой величины инфляции от ежемесячного роста цен =(1+А1)^12. Ячейка B1 должна остаться выделенной. Затем даём команду Данные – ›Работа с данными – ›Анализ «что-если»– ›Подбор параметра. На экране появится диалоговое окно, в котором нужно заполнить 3 строки:

1 – указать адрес ячейки, в которую записана формула,

2 – указать требуемое значение этой формулы,

3 – указать адрес ячейки, где находится изменяемый параметр.

В нашем примере в первой строке диалогового окна появится адрес выделенной ячейки, т.е. нужное значение в ней появится автоматически. Во 2-ю строку надо записать число 1,10 (целая часть от дробной отделяется запятой, а не точкой), а в 3-ю–А1, где находится искомая переменная(рис. 3.26).

Далее следует щёлкнуть мышью по кнопке «Оk», и будет получен ответ 0,008003, т.е. ежемесячный рост цен ~0,8% (рис. 3.27). Очевидно, между величинами, помещёнными в 1-ю и 3-ю строки окна диалога должна существовать функциональная зависимость. Если в качестве изменяемой указать ячейку, содержание которой не влияет на результат, то программа даст ответ Решение не найдено.

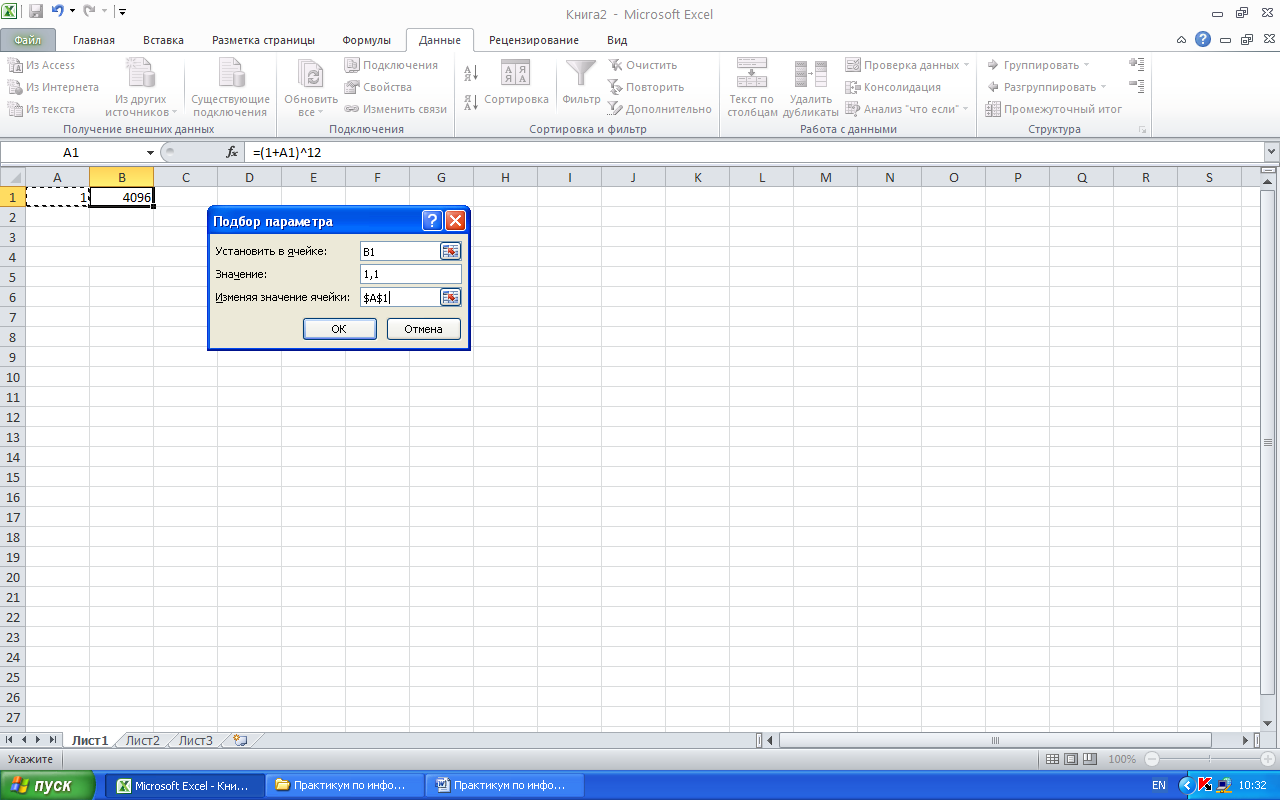
Рис.3.26 Использование функции Подбор параметра

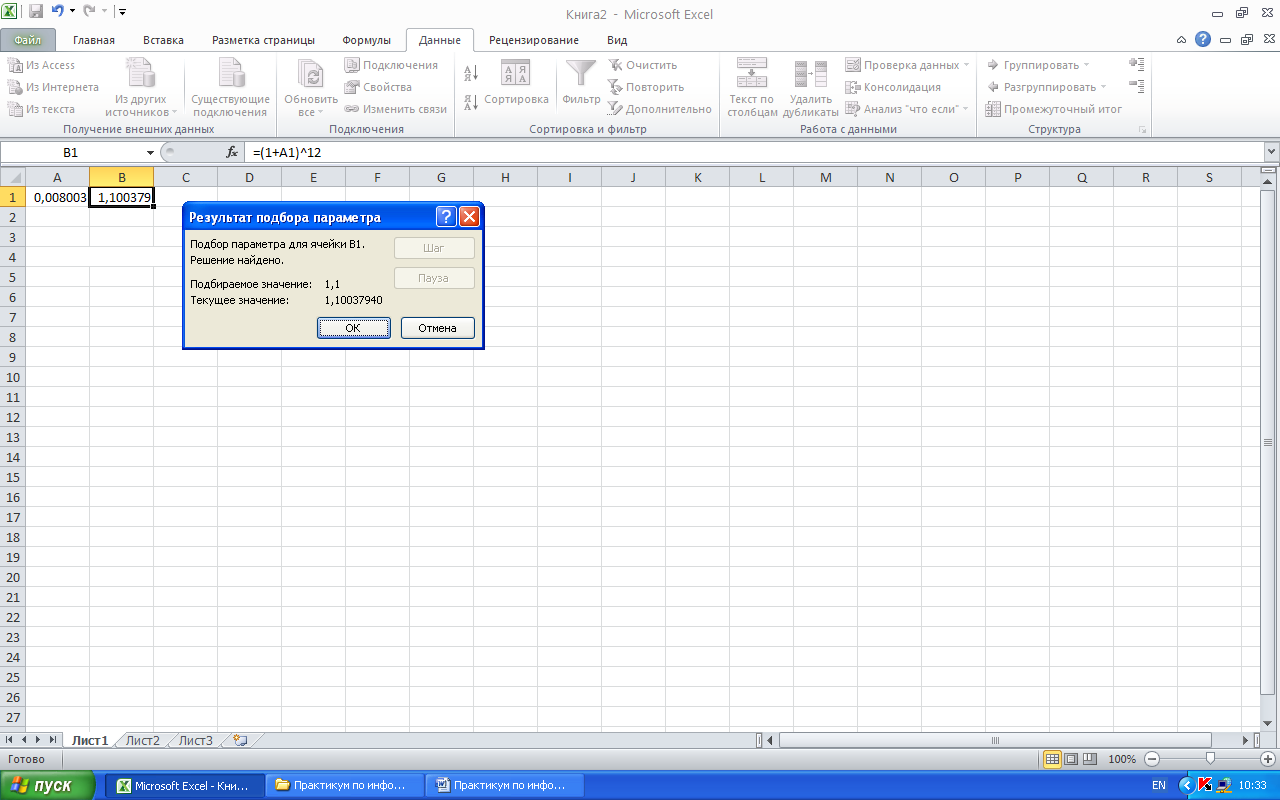
Рис.3.27 Результат использования функции Подбор параметра

Пример второй

Найти корень квадратного уравнения 2*х^2 – 3*x =10.

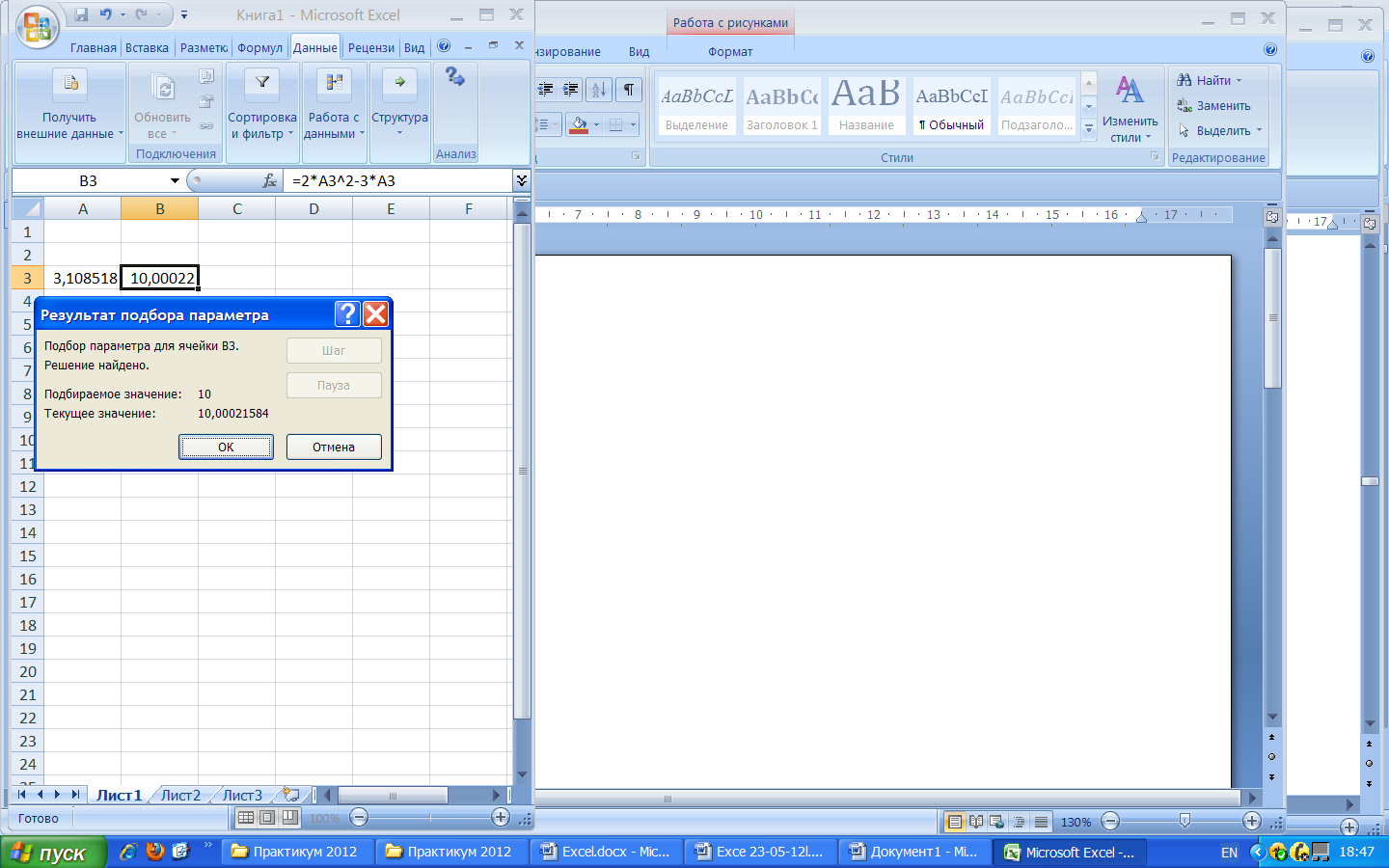
Запишем,например, в А3 предполагаемое значение искомого корня, пусть это будет 1. Запишем в В3 левую часть данного квадратного уравнения. Пройдем: Данные→Работа с данными→Анализ «что если»→Подбор параметра. В первой строке диалогового окна появится В3. Во вторую строку запишем требуемое значение уравнения 10. Втретьей строке укажем адрес ячейки с изменяемым значением искомого корня А3. OK. Результат на рис. 3.28.

Рис.3.28 Нахождение корня квадратного уравнения

Совместное использование различных функций Excel и функции Подбор параметрасущественно расширяет круг решаемых задач.

Рассмотрим, например, совместное использование финансовой функции Будущая стоимость и функции Подбор параметра.

Пример третий

Клиент кладет в банк А рублей под P процентов в год на срок n лет. В конце каждого года клиент снимает со счёта В рублей.

Нужно найти сумму вклада S в конце срока с использованием функции Будущая стоимостьБС(P, n, В, -A, 0).

Пусть клиент кладет в банк 50000 рублей под 12% в год на срок 3года. В конце каждого года клиент снимает со счета 1200 рублей.

Чтобы найти сумму вклада в конце срока с использованием функции БС,ведем на листе Excel (рис.3.29) в столбце А идентификаторы параметров функции, а в столбце В численные значения этих параметров (процентная ставка в виде десятичной дроби, вкладываемая сумма в виде отрицательного числа). Ниже введем саму функцию(f_x, финансовые, БС). Появится окно Аргументы функции, куда последовательно введем адреса аргументов из столбца В.

При заданных аргументах в конце срока получим 66197 рублей.

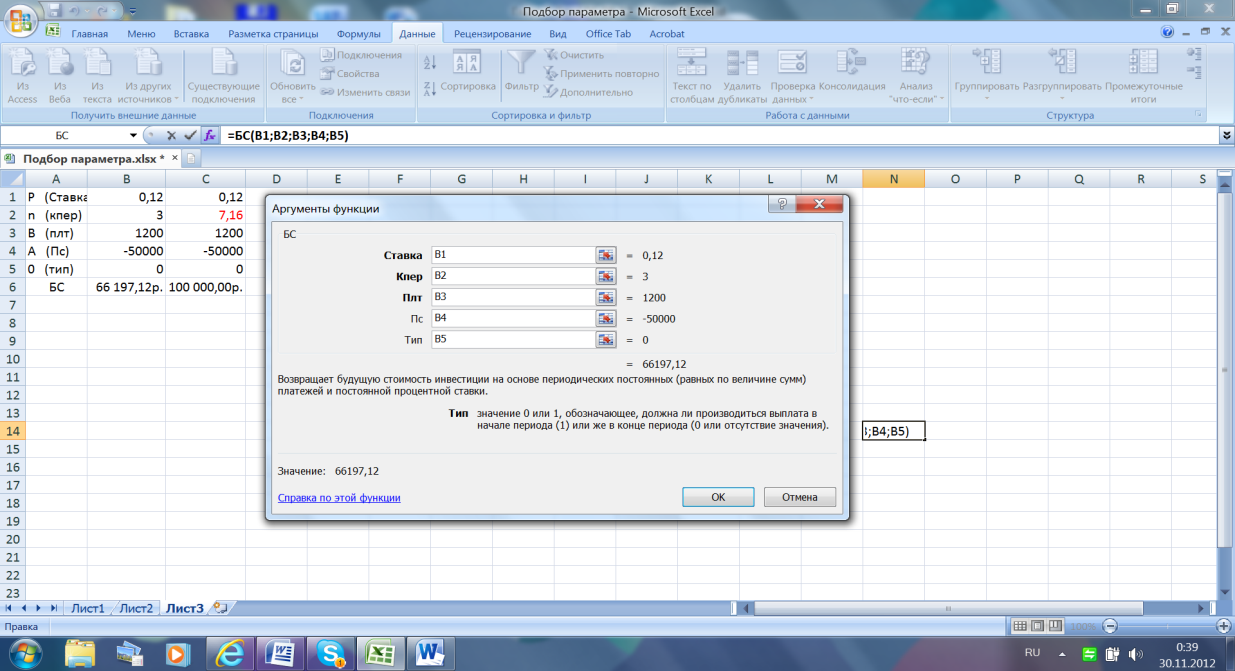
Рис.3.29 Нахождение суммы вклада в конце срока

Для контроля вычислите сумму вклада S в конце срока c использованием обычной алгебраической функции

S=A(1+P)ⁿ–B((1+P)^n-1+(1+P)^n-2+…+(1+P)¹+1).

Пусть теперь нужно узнать, через сколько лет сумма вклада удвоится?

Скопируем данные из столбца В в столбец С. Выделим ячейку С6 и вызовем функцию Подбор параметров. Теперь в С6 нужно получить 100000 рублей изменяя параметр n (количество периодов). Ответ: вложенная сумма удвоится за 7,16 года.

Очевидно, что с помощью функции Подбор параметра можно вычислить любой аргумент функции БС, задав требуемые значения самой функции и остальных аргументов.

Задание 8

1. Составьте произвольное алгебраическое уравнение с одним неизвестным и решите его с помощью функции Подбор параметра.

2. Составьте произвольное тригонометрическое уравнение с одним неизвестным и решите его с помощью функции Подбор параметра (ПП).

3. По данным примера 3 (рис. 3.29, столбец В)с помощью функций БС и ПП найдите:

а) Какую сумму нужно положить в банк, чтобы через 3 года сумма вклада достигла 100000 рублей?

в) Под какой процент нужно положить в банк 50000 рублей, чтобы через 3 года получить 70000 рублей?

с) Какую сумму можно ежегодно снимать со счета, чтобы через 3 года получить (вернуть) вложенные 50000 рублей?

д) Постройте график зависимости суммы вклада S от срока в годах за пять лет.