Розділ v. раціональні числа та дії над ними
ТЕМА 22. ДОДАТНІ І ВІД’ЄМНІ ЧИСЛА
Варіант 1.
Середній рівень
1. 1) Записати числа, протилежні до чисел: –35; 12; 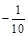 ; 4,5.
; 4,5.
2) Записати координати точок A, B і C,
позначених на координатній прямій.
3) Знайти модулі чисел: 29; –17; 0.
4) Порівняти числа: –20 і 1; –2 і –10.
2.Виконати дії: а) ½–14½ + ½14½; б) ½32½ × ½–2½; в) ½–64½ : ½–8½.
3. 1) Накреслити координатну пряму, взявши за одиничний відрізок одну клітинку, і позначити точки A(–3); B(–5,5); C(2,5) і D(–2,5).
2) Порівняти числа: а) –10,2 і –0,1; б) –4,3 і –5,3; в) –10,4 і –10,5.
Достатній рівень
1. 1) Позначити на координатній прямій числа, модулі яких дорівнюють 4; 7; 3,5.
2) Обчислити значення виразу 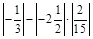 .
.
3) Записати в порядку зростання числа: –3,4; 5,7; –100; 22; –5.
2.Знайти всі цілі розв’язки нерівності –4,3 < x <5,9.
3. Порівняти числа: а) 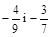 ; б)
; б) 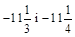 ;
;
Високий рівень
1. 1) Порівняти числа: а) 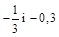 ; б) –1,3 і –1,(3).
; б) –1,3 і –1,(3).
2) Записати всі цілі розв’язки нерівності ½x½ < 6.
3) Записати числа у порядку зростання їх модулів:
–400; –137; 33,21; 590; 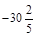 ; –46.
; –46.
2.Скільки цілих розв’язків має нерівність ½x| < 200?
3. Знайти три дроби, які є розв’язками нерівності 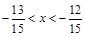 .
.
Варіант 2.
Середній рівень
1. 1) Записати числа, протилежні до чисел: –24; 13; –3,7;  .
.
2) Записати координати точок A, B і C,
позначених на координатній прямій.
3) Знайти модулі чисел: 34; –5,6; 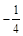 .
.
4) Порівняти числа: –40 і 1; –100 і –150.
2.Виконати дії: а) ½–12½ + ½12½; б) ½–24½ × ½–3½; в) ½–72½ : ½9½.
3. 1) Накреслити координатну пряму, взявши за одиничний відрізок одну клітинку, і позначити точки A(–4); B(–6,5); C(3,5) і D(–3,5).
2) Порівняти числа: а) –13,4 і –0,4; б) –7,6 і –8,6; в) –8,7 і –8,4.
Достатній рівень
1. 1) Позначити на координатній прямій числа, модулі яких дорівнюють 5; 8; 4,5.
2) Обчислити значення виразу 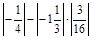 .
.
3) Записати в порядку зростання числа: –4,8; 29; 7; –200; 33.
2.Знайти всі цілі розв’язки нерівності –3,2 < x <4,7.
3. Порівняти числа: а) 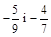 ; б)
; б) 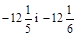 ;
;
Високий рівень
1. 1) Порівняти числа: а) 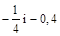 ; б) –2,5 і –2,(5).
; б) –2,5 і –2,(5).
2) Записати всі цілі розв’язки нерівності ½x½ < 5.
3) Записати числа у порядку зростання їх модулів:
–300; 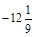 ; 702; –43,2;
; 702; –43,2; 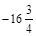 ; –23.
; –23.
2.Скільки цілих розв’язків має нерівність ½x| < 301?
3. Знайти три дроби, які є розв’язками нерівності 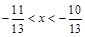 .
.
Варіант 3.
Середній рівень
1. 1) Записати числа, протилежні до чисел: 13; –28; 36; 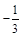 .
.
2) Записати координати точок A, B і C,
позначених на координатній прямій.
3) Знайти модулі чисел: 41; –14; 0.
4) Порівняти числа: –12 і 3; –32 і –42.
2.Виконати дії: а) ½–13½ + ½13½; б) ½24½ × ½–5½; в) ½–88½ : ½–8½.
3. 1) Накреслити координатну пряму, взявши за одиничний відрізок одну клітинку, і позначити точки A(–4); B(–6,5); C(1,5) і D(–1,5).
2) Порівняти числа: а) –5,6 і –7,2; б) –8,5 і 0,5; в) –12,5 і –12,7.
Достатній рівень
1. 1) Позначити на координатній прямій числа, модулі яких дорівнюють 3; 6; 7,5.
2) Обчислити значення виразу 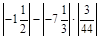 .
.
3) Записати в порядку зростання числа: –5,2; 100; –4; –300; 11.
2.Знайти всі цілі розв’язки нерівності –36 < x <6,7.
3. Порівняти числа: а) 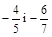 ; б)
; б) 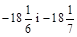 ;
;
Високий рівень
1. 1) Порівняти числа: а) 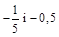 ; б) –3,4 і –3,(4).
; б) –3,4 і –3,(4).
2) Записати всі цілі розв’язки нерівності ½x½ < 4.
3) Записати числа у порядку зростання їх модулів:
–57; 43,41; 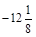 ; –200;
; –200; 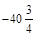 ; 180.
; 180.
2.Скільки цілих розв’язків має нерівність ½x| < 100?
3. Знайти три дроби, які є розв’язками нерівності 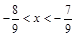 .
.
Варіант 4.
Середній рівень
1. 1) Записати числа, протилежні до чисел: –48; 13; 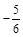 ; 9,2.
; 9,2.
2) Записати координати точок A, B і C,
позначених на координатній прямій.
3) Знайти модулі чисел: 37; –19; 0.
4) Порівняти числа: –11 і 7; –25 і –45.
2.Виконати дії: а) ½–21½ + ½21½; б) ½24½ × ½–3½; в) ½–44½ : ½4½.
3. 1) Накреслити координатну пряму, взявши за одиничний відрізок одну клітинку, і позначити точки A(–4); B(–6,5); C(6,5) і D(–3,5).
2) Порівняти числа: а) –11,5 і –13,4; б) –16,7 і 1,7; в) –16,3 і –16,7.
Достатній рівень
1. 1) Позначити на координатній прямій числа, модулі яких дорівнюють 2; 9; 5,5.
2) Обчислити значення виразу 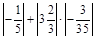 .
.
3) Записати в порядку зростання числа: –200; 12; –13,2; 7; –400.
2.Знайти всі цілі розв’язки нерівності –28 < x <4,6.
3. Порівняти числа: а) 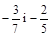 ; б)
; б) 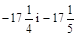 ;
;
Високий рівень
1. 1) Порівняти числа: а) 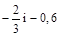 ; б) –2,7 і –2,(7).
; б) –2,7 і –2,(7).
2) Записати всі цілі розв’язки нерівності ½x½ < 7.
3) Записати числа у порядку зростання їх модулів:
500; –68; 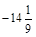 ; 35,32; –400;
; 35,32; –400; 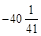 .
.
2.Скільки цілих розв’язків має нерівність ½x| < 151?
3. Знайти три дроби, які є розв’язками нерівності 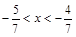 .
.
ТЕМА 23. ДОДАВАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ
Варіант 1.
Середній рівень
Виконати додавання (1 — 3):
1. а) –20 + (–8); б) –20 + (+8); в) 20 + (–8); г) 20 + (–20).
2. а) –0,2 + (0,5); б) –0,2 + (+0,5); в) –0,2 + (+0,1); г) –0,2 + 0,2.
3. 1) а) –2,9 + (–5,4); б) –6,3 + (+2,9); в) –6,3 + (+7,2); г) 12,59 + (–12,59).
2) Обчислити зручним способом: 49,4 + 8,52 + (–39,4) + (–7,52).
Достатній рівень
1. 1) Виконати дії: а) 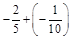 ; б)
; б) 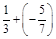 ; в)
; в) 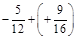 .
.
2) Розв’язати рівняння x – 2,3 = –5,8.
2.Виконати дії: а) –0,13 + 0,17 + (–0,72); б) 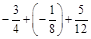 .
.
3. Розв’язати рівняння 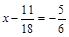 .
.
Високий рівень
1. 1) Виконати дії: а) 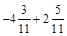 ; б)
; б) 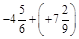 ; в)
; в) 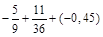
2) Розв’язати рівняння 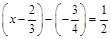 .
.
Розв’язати рівняння (2 — 3):
2.½x½ – ½–13½ = 25.
3. 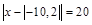 .
.
Варіант 2.
Середній рівень
Виконати додавання (1 — 3):
1. а) –15 + (–4); б) –15 + (+4); в) –15 + (+15); г) –15 + (+20).
2. а) –0,3 + (–0,6); б) –0,3 + 0,3; в) –0,3 + 0,7; г) –0,3 + (–0,5).
3. 1) а) –2,7 + (–3,6); б) –5,2 + (+3,8); в) –8,4 + (–7,5); г) –15,823 + (+15,823).
2) Обчислити зручним способом: 37,2 + 6,57 + (–47,2) + (–5,57).
Достатній рівень
1. 1) Виконати дії: а) 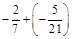 ; б)
; б) 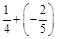 ; в)
; в) 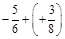 .
.
2) Розв’язати рівняння x – (–3,4) = 5,1.
2.Виконати дії: а) –0,28 + 0,4 + (–0,39); б) 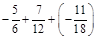 .
.
3. Розв’язати рівняння 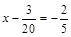 .
.
Високий рівень
1. 1) Виконати дії: а) 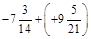 ; б)
; б) 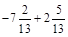 ; в)
; в) 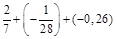
2) Розв’язати рівняння 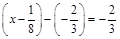 .
.
Розв’язати рівняння (2 — 3):
2.½x½ – ½–14,3½ = 20.
3. 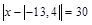 .
.
Варіант 3.
Середній рівень
Виконати додавання (1 — 3):
1. а) –30 + (–7); б) –30 + (+8); в) –40 + (+40); г) 30 + (–20).
2. а) –0,7 + (+0,9); б) –0,7 + (–0,8); в) –0,9 + 0,9; г) –0,2 + 0,7.
3. 1) а) –3,8 + (–4,5); б) –7,2 + (+3,9); в) 6,7 + (–2,8); г) –181,97 + (+181,97).
2) Обчислити зручним способом: 45,12 + 13,18 + (–46,12) + (–12,18).
Достатній рівень
1. 1) Виконати дії: а) 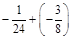 ; б)
; б) 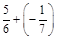 ; в)
; в) 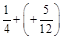 .
.
2) Розв’язати рівняння x – (–4,5) = 6,9.
2.Виконати дії: а) –0,34 + 0,6 + (–0,28); б) 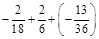 .
.
3. Розв’язати рівняння 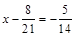 .
.
Високий рівень
1. 1) Виконати дії: а) 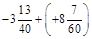 ; б)
; б) 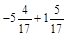 ; в)
; в) 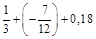
2) Розв’язати рівняння 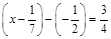 .
.
Розв’язати рівняння (2 — 3):
2.½x½ – ½–12½ = 26.
3. 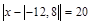 .
.
Варіант 4.
Середній рівень
Виконати додавання (1 — 3):
1. а) –18 + (–2); б) –18 + (+3); в) –27 + (+27); г) 18 + (–29).
2. а) –0,4 + (–0,8); б) –0,4 + (+0,9); в) 0,4 + (–0,5); г) 0,8 + (–0,8).
3. 1) а) –4,3 + (–7,9); б) –8,1 + (+4,6); в) 7,5 + (–4,7); г) –11,129 + (+11,129).
2) Обчислити зручним способом: –49,25 + (+13,67 + (+50,25) + (–16,67).
Достатній рівень
1. 1) Виконати дії: а) 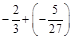 ; б)
; б) 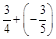 ; в)
; в) 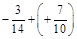 .
.
2) Розв’язати рівняння x – (–8,7) = 9,6.
2.Виконати дії: а) –0,19 + (+3,1) + (–0,22); б) 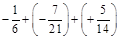 .
.
3. Розв’язати рівняння 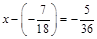 .
.
Високий рівень
1. 1) Виконати дії: а) 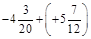 ; б)
; б) 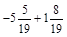 ; в)
; в) 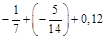
2) Розв’язати рівняння 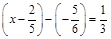 .
.
Розв’язати рівняння (2 — 3):
2.½x½ – ½–15½ = 40.
3. 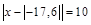 .
.
ТЕМА 24. ВІДНІМАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ
Варіант 1.
Середній рівень
Виконати дії (1 — 3):
1. а) 12 – (–9); б) –15 – (–21); в) 3 – 15; г) –3 – 12.
2. а) –0,4 – (–0,7); б) –1,2 – (–1,4); в) 0,4 – 0,7; г) –0,5 – 0,7.
3. 1) а) 1,23 – (–0,6); б) –17,2 – (–4,8); в) 0,2 – 0,34; г) –0,6 – 0,92.
2) Знайти відстань на координатній прямій між точками A(–2) і B(4).
Достатній рівень
1. 1) Виконати дії: а) 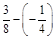 ; б)
; б) 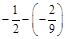 ; в)
; в) 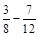 ; г)
; г) 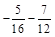 .
.
2) Розв’язати рівняння –4,9 – x = –2,3.
3) Знайти відстань на координатній прямій між точками A(–5,7) і B(–0,8).
Знайти значення виразу (2 — 3):
2. а) –0,7 – 1,23 + 0,98; б) 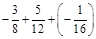 .
.
3. 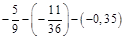 .
.
Високий рівень
1. 1) Виконати дії: а) 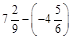 ; б)
; б) 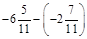 ; в)
; в) 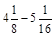
2) Розв’язати рівняння 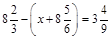 .
.
Розв’язати рівняння (2 — 3):
2.7,2 – ½x½ = –1,8.
3. 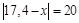 .
.
Варіант 2.
Середній рівень
Виконати дії (1 — 3):
1. а) 18 – (–3); б) –12 – (–8); в) 5 – 17; г) –6 – 19.
2. а) 0,3 – (–0,5); б) –2,4 – (–0,6); в) 0,6 – 0,8; г) –0,6 – 0,8.
3. 1) а) 2,17 – (–0,4); б) –13,5 – (–2,8); в) 0,7 – 0,86; г) –0,5 – 0,73.
2) Знайти відстань на координатній прямій між точками A(–3) і B(6).
Достатній рівень
1. 1) Виконати дії: а) 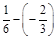 ; б)
; б) 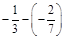 ; в)
; в) 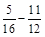 ; г)
; г) 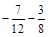 .
.
2) Розв’язати рівняння –3,6 – x = –1,2.
3) Знайти відстань на координатній прямій між точками A(–4,6) і B(–0,9).
Знайти значення виразу (2 — 3):
2. а) 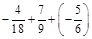 ; б) –0,4 – 2,17 + 0,97.
; б) –0,4 – 2,17 + 0,97.
3. 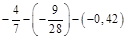 .
.
Високий рівень
1. 1) Виконати дії: а) 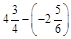 ; б)
; б) 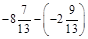 ; в)
; в) 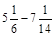
2) Розв’язати рівняння 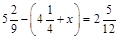 .
.
Розв’язати рівняння (2 — 3):
2.8,4 – ½x½ = –1,4.
3. 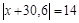 .
.
Варіант 3.
Середній рівень
Виконати дії (1 — 3):
1. а) 16 – (–9); б) –13 – (–5); в) 7 – 12; г) –8 – 12.
2. а) 0,4 – (–0,8); б) –3,3 – (–0,5); в) 0,2 – 0,9; г) –0,5 – 0,7.
3. 1) а) 2,19 – (–0,4); б) –13,3 – (–4,3); в) 0,4 – 0,23; г) –0,6 – 0,84.
2) Знайти відстань на координатній прямій між точками A(–3) і B(8).
Достатній рівень
1. 1) Виконати дії: а) 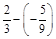 ; б)
; б) 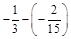 ; в)
; в) 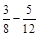 ; г)
; г) 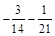 .
.
2) Розв’язати рівняння –3,7 – x = –2,5.
3) Знайти відстань на координатній прямій між точками A(–7,2) і B(–0,5).
Знайти значення виразу (2 — 3):
2. а) 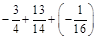 ; б) –0,7 – 1,26 + 0,99.
; б) –0,7 – 1,26 + 0,99.
3. 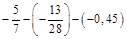 .
.
Високий рівень
1. 1) Виконати дії: а) 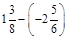 ; б)
; б) 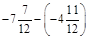 ; в)
; в) 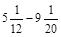
2) Розв’язати рівняння 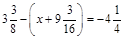 .
.
Розв’язати рівняння (2 — 3):
2.½x½ + ½–40½ = –7.
3. 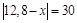 .
.
Варіант 4.
Середній рівень
Виконати дії (1 — 3):
1. а) 11 – (–3); б) –17 – (–28); в) 4 – 13; г) –4 – 11.
2. а) 0,3 – (–0,8); б) –4,1 – (–0,7); в) 0,6 – 0,8; г) –0,4 – 0,9.
3. 1) а) 4,25 – (–0,9); б) –4,2 – (–5,61); в) 0,3 – 0,46; г) –0,3 – 0,89.
2) Знайти відстань на координатній прямій між точками A(–4) і B(7).
Достатній рівень
1. 1) Виконати дії: а) 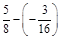 ; б)
; б) 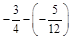 ; в)
; в) 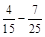 ; г)
; г) 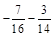 .
.
2) Розв’язати рівняння –6,4 – x = –2,2.
3) Знайти відстань на координатній прямій між точками A(–3,8) і B(–0,9).
Знайти значення виразу (2 — 3):
2. а) 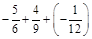 ; б) –0,6 – 1,24 + 0,79.
; б) –0,6 – 1,24 + 0,79.
3. 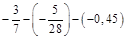 .
.
Високий рівень
1. 1) Виконати дії: а) 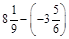 ; б)
; б) 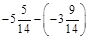 ; в)
; в) 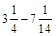
2) Розв’язати рівняння 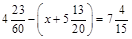 .
.
Розв’язати рівняння (2 — 3):
2.3,5 – ½x½ = –2,6.
3. 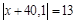 .
.
ТЕМА 25. МНОЖЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ
Варіант 1.
Середній рівень
Виконати дії (1 — 2):
1. а) –20 × (–8); б) –13 × 3; в) (–5)2; г) (–2)3.
2. а) –0,7 × (–0,6); б) 8 × (–0,9); в) –(–0,2)2; г) (–3)4.
3.Знайти значення виразу:
а) –7 × (–4) + (–3); б) 9 × (–5) + 50; в) (–8)2 – 100; г) (–125) × 63(–8).
Достатній рівень
1. 1) Виконати дії: а) 0,4 × (–7,8); б) –0,35 × (–2,5); в) 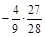 .
.
2) Розв’язати рівняння x : (–2,1) = 4,3.
2.Знайти значення виразу: а) –0,7 × 3 – 6 × (–0,2); б) 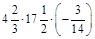 .
.
3. Розв’язати рівняння (x – 5) : (–4) = 3.
Високий рівень
1.Знайти значення виразу:
а) –3,8 × (–1,5) – 0,5 × (–1,2) – 6,5; б) 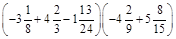 .
.
Розв’язати рівняння (2 — 3):
2.½x½ : (–3) = 2,4.
3. 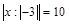 .
.
Варіант 2.
Середній рівень
Виконати дії (1 — 2):
1. а) –15 × (–4); б) –16 × 3; в) (–1)2; г) (–3)3.
2. а) –0,6 × (–0,2); б) 3 × (–0,7); в) (–8)3; г) (–2)4.
3.Знайти значення виразу:
а) –5 × (–7) + (–2); б) –4 × 9 + 12; в) (–10)2 – 120; г) (–25) × 42 × (–4).
Достатній рівень
1. 1) Виконати дії: а) 0,6 × (–8,4); б) –0,75 × (–3,5); в) 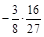 .
.
2) Розв’язати рівняння x : (–4,1) = 2,3.
2.Знайти значення виразу: а) –6 × 0,7 – 4 × (–0,6); б) 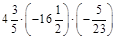 .
.
3. Розв’язати рівняння (x – 3) : (–6) = 7.
Високий рівень
1.Знайти значення виразу:
а) 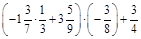 ; б)
; б) 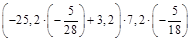 .
.
Розв’язати рівняння (2 — 3):
2.½x½ : (–4) = 2,5.
3. 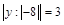 .
.
Варіант 3.
Середній рівень
Виконати дії (1 — 2):
1. а) –40 × (–2); б) –17 × 2; в) 9 × (–4); г) (–3)2.
2. а) –0,9 × (–0,4); б) 4 × (–0,8); в) 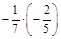 ; г) (–3)4.
; г) (–3)4.
3.Знайти значення виразу:
а) –9 × (–3) + (–8); б) 7 × (–4) + 20; в) (–9)2 – 200; г) 20 × (–42) × (–5).
Достатній рівень
1. 1) Виконати дії: а) 0,6 × (–5,3); б) –0,45 × (–3,5); в) 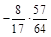 .
.
2) Розв’язати рівняння x : (–20,5) = 5,1.
2.Знайти значення виразу: а) –0,2 × 9 – 4 × (–3,7); б) 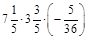 .
.
3. Розв’язати рівняння (x – 3) : (–6) = 8.
Високий рівень
1.Знайти значення виразу:
а) 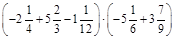 ; б)
; б) 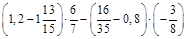 .
.
Розв’язати рівняння (2 — 3):
2.½x½ : (–9) = –4.
3. 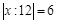 .
.
Варіант 4.
Середній рівень
Виконати дії (1 — 2):
1. а) –15 × (–4); б) –42 × 2; в)(–10)2; г) (–1)3.
2. а) –0,1 × (–0,9); б) 7 × (–0,3); в) 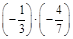 ; г) (–8)3.
; г) (–8)3.
3.Знайти значення виразу:
а) –9 × (–7) + (–4); б) 8 × (–6) + 6,4; в) (–9)2 – 100; г) –8 × 6,8 × (–125).
Достатній рівень
1. 1) Виконати дії: а) 9,3 × (–2,5); б) –0,41 × (–3,7); в) 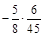 .
.
2) Розв’язати рівняння x : (–5,3) = 2,8.
2.Знайти значення виразу: а) –4,6 × (–2,5) – 0,4 × (–1,5) – 8,3; б) 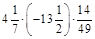 .
.
3. Розв’язати рівняння (x – 7) : (–5) = 20.
Високий рівень
1.Знайти значення виразу:
а) 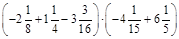 ; б)
; б) 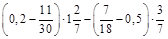 .
.
Розв’язати рівняння (2 — 3):
2.½x½ : (–6) = –8.
3. 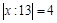 .
.
ТЕМА 26. ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ
Варіант 1.
Середній рівень
Виконати ділення (1 — 2):
1. а) –70 : (–7); б) (–48) : 4; в) 60 :(–5).
2. а) 4,8 : (–4); б) (–6,3) : (–0,9); в) 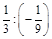 ; г)
; г) 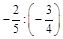 .
.
3.Знайти значення виразу:
а) 48 × (–8) + –5; б) –6,4 : (–0,4) – 17,1; в) 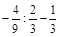 .
.
Достатній рівень
1. 1) Знайти значення виразу: а) 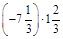 ; б)
; б) 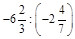 .
.
2) Розв’язати рівняння (–1,2) : x = –3.
2.Знайти значення виразу: а) 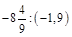 ; б)
; б) 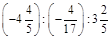 .
.
3. Розв’язати рівняння –54 : (x – 4) = –3.
Високий рівень
1. 1)Знайти значення виразу: а) 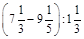 ; б)
; б) 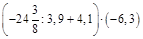 .
.
2) Розв’язати рівняння 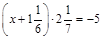 .
.
Розв’язати рівняння (2 — 3):
2.½5x + 2½ = 1.
3. 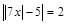 .
.
Варіант 2.
Середній рівень
Виконати ділення (1 — 2):
1. а) –80 : (–8); б) (–63) : 3; в) 52 :(–4).
2. а) 8,2 : (–2); б) (–0,6) : (–0,3); в) 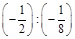 ; г)
; г) 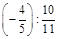 .
.
3.Знайти значення виразу:
а) –7,8 : 8 : (–0,6) – 43,2; б) 7,6 : (–4) – 6,3; в) 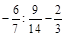 .
.
Достатній рівень
1. 1) Знайти значення виразу: а) 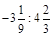 ; б)
; б) 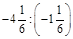 .
.
2) Розв’язати рівняння 0,25x = –1,5.
2.Знайти значення виразу: а) 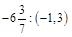 ; б)
; б) 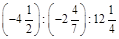 .
.
3. Розв’язати рівняння –49 : (x – 9) = –7.
Високий рівень
1. 1)Знайти значення виразу: а) 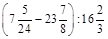 ; б)
; б) 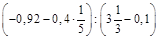 .
.
2) Розв’язати рівняння 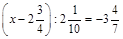 .
.
Розв’язати рівняння (2 — 3):
2.½4x – 7½ = 1.
3. 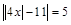 .
.
Варіант 3.
Середній рівень
Виконати ділення (1 — 2):
1. а) –70 : (–7); б) –84 : 7; в) 90 :(–5).
2. а) 6,3 : (–3); б) (–0,8) : (–0,2); в) 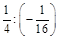 ; г)
; г) 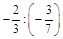 .
.
3.Знайти значення виразу:
а) 18,06 : (–0,6); б) 5,45 : (–0,5); в) 96 : (–3) – 11;.
Достатній рівень
1. 1) Знайти значення виразу: а) 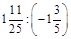 ; б)
; б) 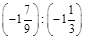 .
.
2) Розв’язати рівняння 0,42x = –8,4.
2.Знайти значення виразу: а) 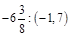 ; б)
; б) 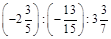 .
.
3. Розв’язати рівняння (x + 4) × (–6) = 72.
Високий рівень
1. 1)Знайти значення виразу:
а) 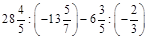 ; б)
; б) 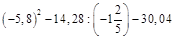 .
.
2) Розв’язати рівняння 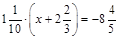 .
.
Розв’язати рівняння (2 — 3):
2.½8x – 7½ = 11.
3. 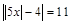 .
.
Варіант 4.
Середній рівень
Виконати ділення (1 — 2):
1. а) –90 : (–9); б) –39 : 3; в) 80 :(–5).
2. а) –6,6 : (–2); б) (–4,5) : 0,5; в) 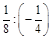 ; г)
; г) 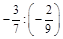 .
.
3.Знайти значення виразу:
а) 15,55 : (–0,5); б) –8,04 : (–0,4); в) 63 : (–9) – 3;.
Достатній рівень
1. 1) Знайти значення виразу: а) 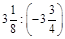 ; б)
; б) 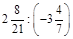 .
.
2) Розв’язати рівняння 0,31x = –9,3.
2.Знайти значення виразу: а) 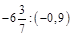 ; б)
; б) 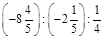 .
.
3. Розв’язати рівняння (x + 3) × (–9) = 6.
Високий рівень
1. 1)Знайти значення виразу:
а) 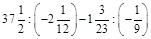 ; б)
; б) 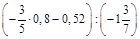 .
.
2) Розв’язати рівняння 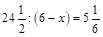 .
.
Розв’язати рівняння (2 — 3):
2.½9x – 5½ = 13.
3. 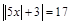 .
.
ТЕМА 27. ПЕРЕТВОРЕННЯ ВИРАЗІВ
Варіант 1.
Середній рівень
1. 1) Розкрити дужки: а) a + (m – n); б) a + (–m + n); в) p – (m – n).
2) Спростити вираз: а) –6a × (–5); б) –6b × 10; в) 7 × с (–10).
3) Розкрити дужки:а) 3 (5х – 4); б) –2 × (–3х + 2); в) (–4х – 3) × (–5).
4) Звести подібні доданки: а) 3а + а; б) –4а – 11а; в) –2 × (–3х + 2).
Спростити вираз (2 –3):
2. а) –2а + 5а – 3; б) 7 – (5 – a); в) –5(3а – 4) + 2а.
3.–4(3а – 2) + 6(2а – 5).
Достатній рівень
1. 1) Спростити вираз 5,2 – (9,3 – b – 2,4).
2) Спростити вираз 2(10b – 3a) – 4(5b + a) і знайти його значення, якщо a = –0,3.
2.Спростити вираз 4(3a – 5b – 7) – 2(6a – 10b) + 3.
3. Користуючись розподільною властивістю множення обчислити значення виразу 52 × 28 – 52 × 29 – 67 × 62.
Високий рівень
1. 1)Спростити вираз 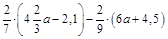 .
.
2) Спростити вираз 0,93y + 0,46y – 1,92y – 0,73y і знайти його значення, якщо y =  .
.
2.Спростити вираз 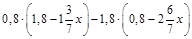 .
.
3. Обчислити розподільним способом значення виразу
3,9 × 2,7 + 3,9 × 7,3 – 1,3 × 3,8 –6,2 × 1,3.
Варіант 2.
Середній рівень
1. 1) Розкрити дужки: а) a + (–b – c); б) x – (–m + n); в) x – (m + n).
2) Спростити вираз: а) –7a × (–3); б) 9 × b × (–8); в) –4m × 3.
3) Розкрити дужки:а) 2 × (3х – 8); б) –3 × (–5х + 4); в) (–7х + 1) × (–8).
4) Звести подібні доданки: а) 5а + а; б) –9а – 2а; в) 4a – 10a.
Спростити вираз (2 –3):
2. а) –4а + 7а – 2; б) 10 – (8 – a); в) –4(2а – 3) + а.
3.–5(4а – 3) + 2(10а + 7).
Достатній рівень
1. 1) Спростити вираз 6,3 – (5,8 – b – 6,2).
2) Спростити вираз 3(8b – a) – 4(6b + a) і знайти його значення, якщо a = –0,2.
2.Спростити вираз 8(3a – 4b – 2) – 2 × (12a – 5b + 7).
3. Користуючись розподільною властивістю множення обчислити значення виразу 43 × 56 + 43 × 21 – 77 × 41.
Високий рівень
1. 1)Спростити вираз 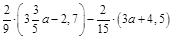 .
.
2) Спростити вираз 0,84y + 0,52y – 1,92y – 0,64y і знайти його значення, якщо y = 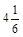 .
.
2.Спростити вираз 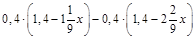 .
.
3. Обчислити розподільним способом значення виразу
4,8 × 2,9 + 4,8 × 17,1 – 14,6 × 2,6 –2,6 × 5,4.
Варіант 3.
Середній рівень
1. 1) Розкрити дужки: а) m + (–a + b); б) y – (–a + b); в) y – (a + b).
2) Спростити вираз: а) –4x × (–8); б) 5 × b × (–12); в) –9 × c × 10.
3) Розкрити дужки:а) 6 × (5x – 2); б) –5 × (–2x + 1); в) (4x – 7) × (–5).
4) Звести подібні доданки: а) 6а + а; б) –5a – 3a; в) 7а – 9а.
Спростити вираз (2 –3):
2. а) –3а + 8а – 4; б) 12 – (a – 8); в) –3(4а – 1) + 10а.
3.–6 × (6а + 5) + 4(9а – 2).
Достатній рівень
1. 1) Спростити вираз –3,4 – (3,1 – c – 1,2).
2) Спростити вираз 5(8b – 3a) + 4(10b + 3a) і знайти його значення, якщо a = –0,2.
2.Спростити вираз 6(3a – 7b – 2) – 9 × (2a – 5b + 3).
3. Користуючись розподільною властивістю множення обчислити значення виразу 68 × 54 + 68 × 25 – 79 × 71.
Високий рівень
1. 1)Спростити вираз 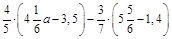 .
.
2) Спростити вираз 1,94y + 0,28 – 1,56 – 1,74y і знайти його значення, якщо y = 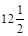 .
.
2.Спростити вираз 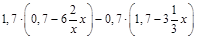 .
.
3. Обчислити розподільним способом значення виразу
6,7 × 8,4 + 6,7 × 1,6 – 2,8 × 7,4 –7,2 × 7,4.
Варіант 4.
Середній рівень
1. 1) Розкрити дужки: а) x + (–a + b); б) x – (a – b); в) x – (–a – b).
2) Спростити вираз: а) –5 × a × (–2); б) 4 × b × (–9); в) –13 × c × (–4).
3) Розкрити дужки:а) 4 × (7a – 2); б) –4 × (–7х + 3); в) (–2х + 5) × (–6).
4) Звести подібні доданки: а) –5а + 9а – 3; б) –20 – (2 – а); в) –8 × (2a – 3) + 10a.
Спростити вираз (2 –3):
2. а) –5а + 9а – 3; б) –20 – (2 – a); в) –8(2а – 3) + 10а.
3.–7(4а – 5) + 14(2а + 3).
Достатній рівень
1. 1) Спростити вираз –2,9 – (0,2 – x + 0,7).
2) Спростити вираз 5(8b – 3a) + 4(10b + 3a) і знайти його значення, якщо a = –0,2.
2.Спростити вираз 6 × (3a – 7b – 2) – 9 × (2a – 5b + 3).
3. Користуючись розподільною властивістю множення обчислити значення виразу 68 × 54 + 68 × 25 – 79 × 71.
Високий рівень
1. 1)Спростити вираз 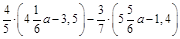 .
.
2) Спростити вираз 1,94y + 0,28y – 1,56 – 1,74y і знайти його значення, якщо y = 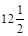 .
.
2.Спростити вираз 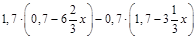 .
.
3. Обчислити розподільним способом значення виразу
6,7 × 8,4 + 6,7 × 1,6 – 2,8 × 7,4 – 7,2 × 7,4.
ТЕМА 28. РІВНЯННЯ
Варіант 1.
Середній рівень
Розв’язати рівняння:
1. а) x + 4 = –7; б) x – 8 = –12; в) 4x = –10; г) –5x = –100.
2. а) 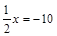 ; б)
; б) 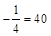 ; в) 7x + 3 = 0; г) 8x = 3x + 30.
; в) 7x + 3 = 0; г) 8x = 3x + 30.
3.4x + 7 = 27 – x.
Достатній рівень
Розв’язати рівняння:
1. а) 0,7x – 3,1 = 0,2x + 7,4; б) 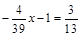 .
.
2.8(x + 1) – 3(x + 1) = 11.
3. 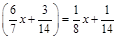 .
.
Високий рівень
Розв’язати рівняння:
1. а) 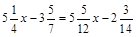 ; б)
; б) 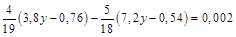 .
.
2. 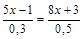 .
.
3. 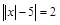 .
.
Варіант 2.
Середній рівень
Розв’язати рівняння:
1. а) x + 10 = –8; б) x – 7 = –15; в) 2x = –16; г) –8x = –88.
2. а) 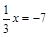 ; б)
; б) 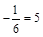 ; в) 10x + 30 = 0; г) 4x = x + 15.
; в) 10x + 30 = 0; г) 4x = x + 15.
3.8x – 11 = 13 – 2x.
Достатній рівень
Розв’язати рівняння:
1. а) 0,7x + 3,6 = 0,2x + 8,1; б) 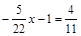 .
.
2.5(x – 3) – 21(x + 7) = 1.
3. 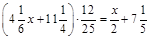 .
.
Високий рівень
Розв’язати рівняння:
1. а) 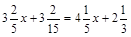 ; б)
; б) 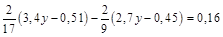 .
.
2. 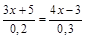 .
.
3. 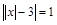 .
.
Варіант 3.
Середній рівень
Розв’язати рівняння:
1. а) x + 15 = –2; б) x – 10 = –2; в) 3x = –21; г) –7x = –70.
2. а) 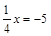 ; б)
; б) 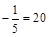 ; в) 5x – 2 = 0; г) 6x = x + 25.
; в) 5x – 2 = 0; г) 6x = x + 25.
3.7x – 14 = 6 – 3x.
Достатній рівень
Розв’язати рівняння:
1. а) 0,5x + 2,4 = 0,2x + 3,6; б) 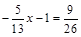 .
.
2.7(x – 2) – 21(x + 4) = 3.
3. 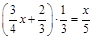 .
.
Високий рівень
Розв’язати рівняння:
1. а) 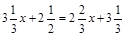 ; б)
; б) 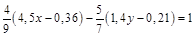 .
.
2. 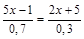 .
.
3. 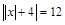 .
.
Варіант 4.
Середній рівень
Розв’язати рівняння:
1. а) x + 3 = –20; б) x – 8 = –4; в) 5x = –50; г) –7x = 28.
2. а) 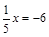 ; б)
; б) 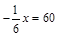 ; в) 7x + 49 = 0; г) 7x = 4x + 21.
; в) 7x + 49 = 0; г) 7x = 4x + 21.
3.9x – 3 = 7 + 5x.
Достатній рівень
Розв’язати рівняння:
1. а) 8x + 4,2 = 0,6x – 3,6; б) 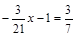 .
.
2.9(x + 2) – 5(x – 3) = –7.
3. 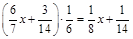 .
.
Високий рівень
Розв’язати рівняння:
1. а) 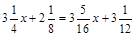 ; б)
; б) 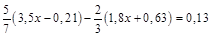 .
.
2. 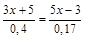 .
.
3. 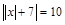 .
.
ТЕМА 29. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ РІВНЯНЬ
Варіант 1.
Середній рівень
1. 1) Одне з чисел на 17 більше, ніж друге, а їх сума дорівнює 53. Знайти менше з цих чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел через х).
2) Одне з додатних чисел у 7 разів більше за друге, а сума цих чисел дорівнює 88. Знайти менше з цих чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел че6рез x).
2.Одне з додатних чисел у три рази більше, ніж друге. Знайти ці числа, якщо їх різниця дорівнює 120.
3.У двох бригадах працює 106 чоловік, причому у першій на 12 чоловік більше, ніж у другій. Скільки чоловік в кожній бригаді?
Достатній рівень
1.Затри дні туристи пройшли 66 км. За другий день вони пройшли на 8 км більше, ніж за перший. Скільки кілометрів проходили туристи кожногодня?
2.На першій полиці книг у 4 рази більше, ніж на другій. Після того, як з першої полиці перенесли на другу 24 книги, на обох полицях книг стало порівну. Скільки книг було на кожній полиці спочатку?
3. Задану кількість деталей робітник може виготовити на три дні раніше, ніж учень. За один день робітник виготовляє 15 деталей, а його учень — 10 деталей. За скільки днів виготовить задану кількість деталей учень?
Високий рівень
1.У першій бригаді було в 4 рази менше робітників, ніж у другій. Після того, як з другої бригади 10 чоловік перевели у першу, у першій стало у 2 рази менше робітників, ніж у другій. Скільки робітників було в кожній бригаді спочатку?
2.70% першого додатного числа дорівнюють 120% другого додатного числа. Знайти ці числа, якщо їх різниця дорівнює 50.
3. Батько старший від сина в 5 разів, а сума їх років дорівнює 30. Через скільки років батько стане старшим від сина в 2 рази?
Варіант 2.
Середній рівень
1. 1) Одне з чисел на 9 менше, ніж друге. Менше з чисел позначено через x. Виразити через x більше число.
а) x – 9; б) x + 9; в) x : 9; г) 9x.
2) Одне з додатних чисел у 3 рази більше, ніж друге. Менше з чисел позначено через x. Виразити через x більше число.
а) x – 3; б) x + 3; в) x : 3; г) 3x.
2.Одне з додатних чисел у 5 разів більше, ніж друге. Знайти ці числа, якщо їх різниця дорівнює 440.
3.Площа двох ділянок дорівнює 140 га. Знайти площу кожної ділянки, якщо площа першої на 18 га більша, ніж площа другої.
Достатній рівень
1.Книгу, в якій 136 сторінок тексту, хлопчик прочитав за три дні. За другий день він прочитав у 2 рази більше сторінок, ніж за перший, і на 6 сторінок менше, ніж за третій. Скільки сторінок книги ппочитав учень за перший день?
2.У двох автобусах було 78 туристів. Після того, як з першого автобусу в другий перейшли 4 туристи, їх стало в автобусах порівну. Скільки туристів було спочатку в кожному з автобусів?
3. Відстань між містами A і B автомобіль проїждає на 4 год раніше, ніж велосипедист. Швидкість руху автомобіля 75 км/год, а велосипедиста — 25 км/год. За скільки часу проїхав відстань між містами автомобіль і велосипедист?
Високий рівень
1.У першому мішку було в 3 рази більше борошна, ніж в другому. Після того, як з першого мішка взяли 20 кг борошна, а з другого — 10 кг, у першому мішку стало в 4 рази більше борошна, ніж у другому. Скільки кілограмів борошна було у кожному мішку спочатку?
2.0,8 першого додатного числа дорівнюють 0,3 другого числа. Знайти ці числа, якщо їх різниця дорівнює 20.
3. 3 роки тому назад батько був старший від сина у 11 разів. Скільки років нині батькові, якщо через 5 років батько буде старший від сина в 3 рази?
Варіант 3.
Середній рівень
1. 1) Одне з чисел на 25 більше, ніж друге, а їх сума дорівнює 103. Знайти менше з чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел через x).
2) Одне з додатних чисел у 8 разів менше за друге, а сума цих чисел дорівнює 144. Знайти менше з цих чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел через x).
2.Одне з чисел на 2,6 більше, ніж друге. Знайти ці числа, якщо їх сума дорівнює 28,8.
3.У першому мішку у 3 рази більше цукру, ніж у другому. Скільки кілограмів цукру у кожному мішку, якщо в першому на 18 кг більше, ніж у другому?
Достатній рівень
1.За три дні туристи пройшли 56 км. За другий день вони пройшли в 2 рази менше, ніж за перший, і на 8 км менше ніж за третій. Скільки кілометрів пройшли туристи за другий день?
2.У першій бригаді було у 3 рази більше робітників, ніж у другій. Після того, як з першої бригади перевели 25 чоловік у другу, в обох бригадах стало робітників порівну. Скільки робітників було спочатку в кожній бригаді?
3. Перша друкарка може передрукувати рукопис на 2 год раніше , ніж друга. За годину перша друкарка друкує 12 сторінок, а друга — 10 сторінок. За скільки часу може передрукувати даний рукопис друга друкарка?
Високий рівень
1.На першій ділянці було у 5 разів більше кущів смородини, ніж на другій. Коли з першої ділянки пересадили 40 кущів на другу, то на першій стало в 2 рази більше, ніж на другій. Скільки кущів було на кожній ділянці спочатку?
2.З пункту А в пункт В виїхав автобус. Через 1,5 год слідом за ним виїхав легковий автомобіль, швидкість якого на 30 км/год більша, ніж швидкість автобуса. Через 4 год після свого виїзду легковий автомобіль був на 30 км ближче до пункту B, ніж автобус. Знайти швидкість легкового автомобіля.
3. З пункту A в пункт B виїхав велосипедист, швидкість якого 20 км/год. Через 20 хвилин назустріч йому з пункту B виїхав мотоцикліст зі швидкістю 60 км/год. Відстань між пунктами дорівнює 140 км. Яку відстань проїхав до зустрічі мотоцикліст?
Варіант 4.
Середній рівень
1. 1) Одне з чисел на 14 більше, ніж друге, а їх сума дорівнює 86. Знайти менше з цих чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел через x).
2) Одне з додатних чисел у 9 разів менше за друге, а сума цих чисел дорівнює 430. Знайти менше з цих чисел. (Розв’язати задачу за допомогою рівняння, позначивши менше з чисел через x).
2.Одне з чисел на 11,3 менше, ніж друге. Знайти ці числа, якщо їх сума дорівнює 47,7.
3.У сплаві, що складається з міді і срібла, міді у 3 рази більше, ніж срібла. Скільки кілограмів срібла у сплаві, якщо його на 1,4 кг менше?
Достатній рівень
1.За три дні зорали 12 га поля. За третій день зорали у 2 рази менше, ніж за перший, та на 8 га більше, ніж за другий. Скільки гектарів зорали за третій день?
2.У першій пачці було у 2 рази менше зошитів, ніж у другій. Після того, як з першої пачки взяли 28 зошитів, а з другої — 7 зошитів, в обох пачках зошитів стало порівну. Скільки зошитів було спочатку в кожній пачці?
3. Одне з додатних чисел на 60% більше від другого. Знайти ці числа, якщо їх сума дорівнює 78?
Високий рівень
1.У першій пачці було у три рази більше зошитів, ніж у другій. Після того, як їз другої пачки переклали в першу 10 зошитів, то у другій — стало зошитів у чотири рази менше, ніж в першій. Скільки зошитів було в кожній пачці спочатку?
2.З пункту А в пункт В виїхаввелосипедист. Через 0,5 год слідом за ним виїхавмотоцикліст, швидкість якого на 40 км/год більша, ніж швидкість велосипедиста. Через 2,5 год після відправлення мотоцикліст проїхав на 90 км більше, ніж велосипедист. Знайти швидкість велосипедиста.
3. З пункту A в пункт B виїхав пасажирський поїзд, швидкість якого 60 км/год. Через 40 хвилин назустріч йому з пункту B виїхав швидкий поїзд зі швидкістю 90 км/год. Відстань між пунктами дорівнює 390 км. Яку відстань проїхав до зустрічі пасажирський поїзд?
ТЕМА 30. КООРДИНАТНА ПЛОЩИНА
Варіант 1.
Середній рівень
1.Записати координати точок:
1) A, B, C і D, зображених на рисунку;
2) M, N, K і L, зображених на рисунку.
Накреслити систему координат:
3) A(3; 2), B(4; –5), C(–4; –2) і D(–1; –4).
4) M(2; 0), N(0; 3), K(–6; 0) і P(0; –5).
2.Із точок A(1; 91), B(0; –300), C(200; 0), D(19,5; 1), E(–40; 0) і K(0; 50) виписати ті, що: а) належать вісі x; б) належать вісі y.
3.Побудувати в координатній площині прямокутник ABCD, з координатами вершин A(–2; –1), B(–2; 5), C(7; 5) і D(7; –1). За рисунком знайти довжини сторін і обчислити периметр та площу прямокутника.
Достатній рівень
1.На координатній площині побудувати пряму, що проходить через точки A(0; 3) і B(4; 3). За рисунком встановити, які з точок M(0; 2), L(1; –2); K(–2; 6) і L(–2; 2) належать цій прямій, а які не належать.
2.На координатній площині побудувати трикутник ABC з координатами вершин
A(–2; 2), B(–1; 6) і C(3; 2). Провести висоту BM, записати координати точки Mю За рисунком знайти довжину AC і BC та обчислити площу трикутника ABC.
3. На координатній площині позначити три точки, ординати яких дорівнюють –4. Яку фігуру утворюють усі точки площини, в яких ордината дорівнює –4. Накреслити цю фігуру.
Високий рівень
1. 1)На координатній площині зобразити фігуру, для координат точок якої виконується рівність x = 3.
