Механические модели идеализированных тел

Необходимо отметить, что все законы реологии разработаны для идеальных тел. Известны три основные модели идеализиро­ванных материалов: идеально упругое тело (по Гуку), идеально пластическое тело (по Сен-Венану), идеально вязкая жидкость (по Ньютону).

Механической моделью вязкой жидкости являет­ся демпфер (рис. 13.1, а), или тело Ньютона. Идеально вязкая жидкость характеризуется тем, что напряжения в ней пропорци­ональны скорости деформации.

Вязкое течение происходит под действием любых сил, как бы малы они ни были, однако скорость деформации при уменьше­нии сил уменьшается, а при их исчезновении обращается в нуль.

Моделью упругого твердого тела является пружина (рис. 13.1, б), или тело Гука. Идеально упругое тело — это систе­ма, в которой энергия, затраченная на деформацию, накаплива­ется в теле и может быть возвращена при разгрузке.

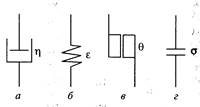Рис. 13.1. Механические модели, отражающие простые реологические свойства материалов:

а - тело Ньютона;

б — тело Гука;

в — тело Сен-Венана;

г — тело Рэнкина

Модель идеально пластичного тела изображает­ся в виде пары трения и определяется как тело Сен-Венана (рис. 13.1, в). Оно неподатливо при нагрузке ниже предела теку­чести, а после его превышения неограниченно деформируется. Предел текучести — это реологическая константа элемента пла­стичности. При изучении структурно-механических свойств пи­щевых продуктов их испытывают на разрушение, которому пред­шествуют мгновенные необратимые деформации.

Модель твердого тела, или тело Рэнкина, изображается как пара сцепленных пластин (рис. 13.1, г). Реологическая кон­станта данного элемента — предел прочности. Если при осевом нагружении достичь предела прочности, сцепленные пластины необратимо разъединяются.

Необходимо отметить, что ни один из реальных пищевых про­дуктов не может быть полностью описан ни одной из моделей идеальных тел. В большинстве своем пищевые продукты соответ­ствуют сложным моделям, представляющим собой комбинацию простых, т. е. являются упругопластичными, упруговязкими или вязкопластичными телами, причем в зависимости от условий (температуры, влажности, давления, способа и скорости приложе­ния нагрузки) превалируют то одни, то другие свойства. В связи с этим при изучении реологических свойств продукта обязательно должны быть четко указаны условия проведения испытаний, в противном случае полученные результаты будут несопоставимы.

Свойства жидкостей

К жидкостям относятся вещества, у которых при постоянном напряжении сдвига θ наблюдается течение (деформация ε) с посто­янной или переменной скоростью. Свойства жидкостей могут про­являться и у пластичных тел после превышения предела текучести.

При простом течении ньютоновской жидкости с напряжени­ем θ возникает деформация с определенной скоростью сдвига γ. Отношение напряжения сдвига к скорости деформации сдвига является реологической константой жидкости и называется ньютоновской вязкостью η:

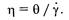
Для неньютоновских жидкостей вязкость является функцией скорости сдвига, поэтому ее называют «кажущейся» или эффек­тивной вязкостью η_Эф (Па • с), которая достаточно полно харак­теризует поведение текучего материала.

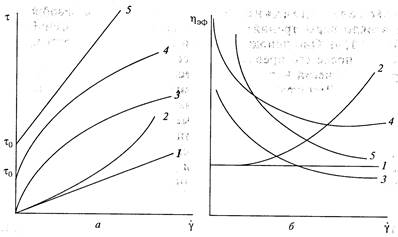
Рис. 13.2. Неполные кривые течения (а) и функции вязкости (б):

1 — ньютоновской жидкости;

2 — дилатантной жидкости;

3 — структурно-вязкой жидкости;

4— нелинейного пластичного тела;

5— линейного пластичного тела

Определение эффективной вязкости предусматривает изме­рение значений (θ, γ) в широкой области у для построения кри­вой течения и функции вязкости.

Для характеристики жидкостей используют кривые тече­ния — реограммы, представляющие собой графическую зави­симость напряжения сдвига от скорости деформации в условиях простого сдвига.

Реограмма ньютоновских жидкостей представляет собой пря­мую линию 1 (рис. 13.2), проходящую через начало координат. Все кривые течения 2-5, которые отклоняются от прямой ли­нии, соответствуют неньютоновским жидкостям. При этом кри­вая 2 отражает дилатантное течение, характерное в основном для концентрированных дисперсных систем, при котором с увеличе­нием скорости деформации наступает «затруднение сдвига» (при высокой концентрации дисперсной фазы вследствие образова­ния пространственной структуры возникает предел текучести); кривая 3 — псевдопластичное течение, что характерно для «сдви­гового размягчения» вследствие разрушения структуры с увели­чением скорости деформации; кривая 4 — нелинейное пластич­ное течение, характерное для большинства пластичных тел.

Линейный участок кривой 5 характерен для бингамовских тел и соответствует идеальному пластичному течению.

Таким образом, эффективная вязкость неньютоновских жид­костей состоит из двух компонентов:

1 — неньютоновской вязкости η_∞, основанной на внутрен­нем трении жидкости и представляющей собой физическую кон­станту материала;

2— структурного сопротивления η_Эф (γ) — η_Эф, зависящего от структурного состояния дисперсных систем и являющегося фун­кцией скорости сдвига γ.

Свойства твердых тел

Твердые тела в зависимости от упругости бывают гуковскими и негуковскими.

Гуковское тело — это идеально упругое тело, состояние кото­рого описывается уравнением Гука

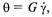где G — модуль упру гости.

После снятия нагрузки, отдавая накопленную энергию, гуков­ское тело без запаздывания возвращается в исходное состояние.

Однако среди твердых тел встречаются такие, поведение ко­торых не соответствует поведению идеально упругого тела. Такие тела называются негуковскими.

Для негуковского твердого тела с нелинейной упругостью

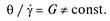
При этом модуль сдвига является функцией деформации, что характерно, например, для пористых пенообразных пищевых материалов. В связи с этим, как и для неньютоновских жидко­стей, вводят понятие эффективного модуля упругости G_Эф. Если напряжение не превышает предела текучести (или прочности) твердого тела, соотношение между напряжением сдвига и дефор­мацией описывается уравнением

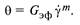
На рис. 13.3 приведены графики зависимости деформации ε от времени деформирования τ при постоянном напряжении для твердых, твердообразных, жидких и жидкообразных структур пищевых продуктов.

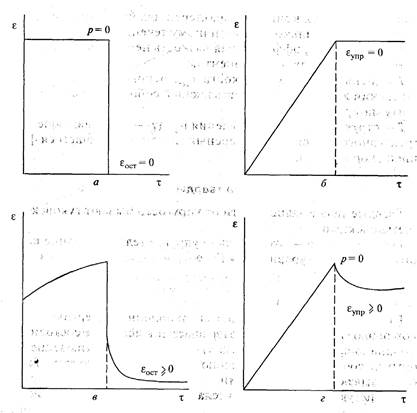
Рис. 13.3. Схема зависимости деформации ε от времени τ при постоянном напряжении

Для идеально твердых тел (рис. 13.3, а) основной характери­стикой является модуль упругости, определяемый по величине упругой, исчезающей после снятия напряжений деформации ε_упр. Определить вязкость твердого тела не представляется воз­можным из-за отсутствия у него пластической остаточной дефор­мации (ε_ост= 0).

Измерение величины упругих деформаций и модулей у неко­торых твердых (кристаллических) структур также связано со зна­чительными трудностями из-за малой величины этой деформа­ции, хрупкости. Для таких тел определяют прочность или крити­ческое напряжение разрушения структуры. При этом испытуемый образец нагружают постепенно, увеличивая напряжение до кри­тического, соответствующего разрушению структуры. В структуре постепенно развиваются дефекты (например, трещины). Крити­ческое напряжение, или прочность, бывает значительно меньше, чем модуль упругости, определенный по величине мгновенной упругой деформации, протекающей в доли секунды.

У идеальных, или истинных, жидкостей (рис. 13.3, б) пред­ставляется возможным определить только вязкость, так как вся получаемая деформация является остаточной (ε_оct = 0) и после снятия нагрузки не исчезает.

У идеально твердых тел и жидкостей по указанным выше при­чинам нельзя определить период релаксации напряжений.

У большинства продуктов можно определить как упругие, так и остаточные деформации и по ним рассчитать модули упруго­сти, вязкость и период релаксации. На рис. 13.3, в представлен пример для твердообразных, а на рис. 13.3, г — для жидкообраз-ных продуктов.

Таким образом, многочисленные реальные твердые тела об­ладают мгновенной обратимой упругостью и запаздывающей уп­ругостью, а после превышения предела текучести возникает пла­стичное течение.

Пищевые продукты и полуфабрикаты, такие, как тесто, тво­рожные массы, мясные и рыбные фарши, мясо, шпик, фруктовые и овощные пюре, джемы, повидло, сливочное масло и маргари­ны, кремы, относятся к пластично-вязким твердообразным структурами, и их деформационное поведение, или течение, от­личается от поведения ньютоновских жидкостей или твердых тел.

Для неразрушенных структур существует два основных типа кривых кинетики деформации.

В первом случае (рис. 13.4, а) приложенное напряжение меньше предела текучести (Р<Р_т). Этот тип встречается очень редко, например, при действии малых напряжений на пищевые студни деформация может быть полностью обратимой.

При мгновенном действии напряжения возникает упругая де­формация 80 как мгновенная реакция тела на внешнее воздейст­вие О А. Ее величина определяется силами первичных химиче­ских связей. Вслед за мгновенной, упругой развивается уже во времени высокоэластичная деформация, также обратимая по ве­личине А С. Ее величина характеризует силу связи между отдель­ными макромолекулами и их звеньями. Деформация достигает некоторого максимального значения ε_mах и далее не меняется, так как действующее напряжение уравновешивается силами внутреннего сопротивления тела, конечный участок кривой яв­ляется линейным. В точке С напряжение снимают (Р = 0), де­формация спадает до нуля по кривой CDF, система полностью восстанавливает свою форму.

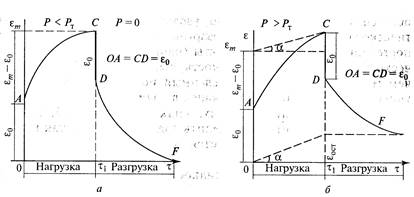
В большинстве случаев для реальных пищевых систем прило­женное напряжение превышает предел текучести (Р> Р_т) и полу­чается кривая, изображенная на рис. 13.4, б.

При мгновенном действии напряжения возникает упругая деформация ε₀ как мгновенная реакция тела на внешнее воздей­ствие.

После возникновения мгновенной упругой деформации об­наруживается непрерывное нарастание остаточной деформации, переходящее в пластическое течение. Остаточная деформация нарастает с постоянной скоростью, которую можно охарактери­зовать tg α, a максимальная деформация ε_mах за время действия нагрузки τ определяется отрезком, отсекаемым на оси ординат касательной к конечному участку кривой.

В точке С напряжение снимают, происходит своеобразный «отдых» образца, при этом упругая деформация исчезает.

ε₀ = ОА = CD, и идет восстановление эластической деформа­ции. С увеличением времени кривая DF будет приближаться к некоторому конечному значению остаточной деформации ε_ост.

По кривой кинетики деформации кроме предела упругости можно найти модули мгновенной упругости сдвига, эластично­сти и другие характеристики.