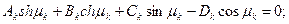Выражение для формы свободных колебаний пластины

Свободно опертая пластина. Точное решение уравнения (3.193) может быть получено лишь для некоторых сравнительно простых вариантов закрепления сторон опорного контура пластины. Так, в случае свободно опертой пластины можно удовлетворить точно всем граничным условиям, если принять для функции wn (x, у) выражение вида:

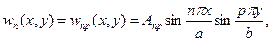(3.9)

где а и b — размеры пластины в плане.

Общее выражение для определения значений частот свободных колебаний пластины.

Подставив выражение (3.9) в уравнение (3.8), из условия неравенства нулю коэффициента Апр получим уравнение для определения частот λпр рассматриваемой свободно опертой пластины:

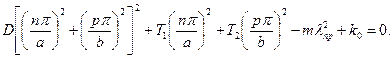
Откуда

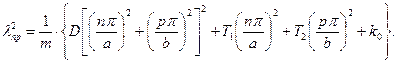(3.10)

3.11. Расчёт значения частоты первого тона (n=1;p=1) свободных колебаний пластины при отсутствии действия усилий в срединной плоскости.

Интенсивность нагрузки на пластину от её веса и присоединённых масс воды:

p = p_пл+ p_в = γ_сh + к γ в = 7,85·10³·0,020 + 0,47·1,025·10³·0,95 = 614,7 кгс/м²

Найдем интенсивность массы с учетом интенсивности нагрузки на пластину от её веса и присоединённых масс воды:

,

.

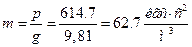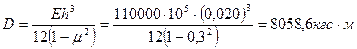Пр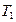и и 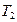равно 0:

.

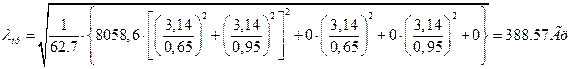3.12. Расчёт значения частоты первого тона (n=1;p=1) свободных колебаний пластины при действии усилий в срединной плоскости только в направлении «ox»

,

.

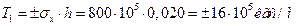Тогда при Т₁^/ = 0,5Т₁ («+» - растяжение):

,

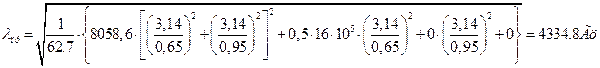при Т₁^/ = 0,5Т₁ («-» - сжатие):

,

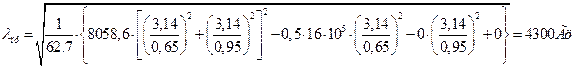Расчёт значения частоты первого тона свободных колебаний пластины при отсутствии действия усилий в срединной плоскости.

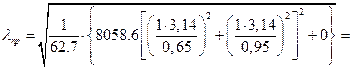387.93 Гц

Сопоставление результатов расчётов. Выводы.

При растяжении частота колебаний больше, чем при сжатии, а при Т₁ и Т₂ равном «0» (отсутствие усилия в средней части пластины) частота колебаний лежит между растяжением и сжатием.

РАЗДЕЛ 4 «Общая вибрация корабля. Вибрация корпуса как призматической безопорной свободной балки.»

4.1 Расчётная схема, рис.4

Исходные данные.

№   п/п	Длина балки "l" м	Интен сивность веса балки "q" кгс/cм	Модуль упругости материала "Е" МПа	Момент инерции поперечного сечения "I" м4
				16.0

Дифференциальное уравнение свободных колебаний упругой системы.

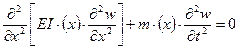(4.1)

Общее решение колебаний упругой системы.

Как и ранее при исследовании свободных колебаний упругой системы решение (2.1) будем искать в виде:

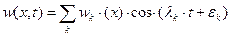(4.2)

Дифференциальное уравнение для форм главных свободных колебаний .

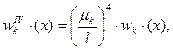(4.3)

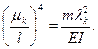где (4.4)

Общий интеграл дифференциального уравнения для форм главных свободных колебаний.

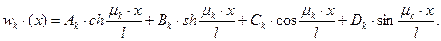(4.5)

Граничные условия по концам безопорной свободной балки.

x=0, l: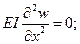

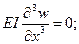
4.8 Граничные условия для форм свободных колебаний по концам безопорной свободной балки:

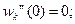
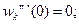
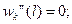
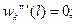(4.6)

Составление уравнений из условий подчинения граничным условиям на левом и правом концах балки.

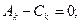
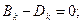
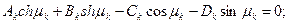(4.7)