Проблема учета «наследственной» силы Бассе и обзор работ, посвященной этой проблеме

СОДЕРЖАНИЕ

Аннотация…………………………………………………………………………2

Список основных обозначений…………………………………………………..3

Введение…………………………………………………………………………...4

1.1. Проблема учета «наследственной» силы Бассе и обзор работ, посвященной этой проблеме…………………………………………………….4

1.1.1. Обзор экспериментальных исследований силы Бассе при движении частицы дисперсной фазы с нулевой начальной скоростью…………………8

1.2. Экспериментальная установка и методика исследования, применяемые в НИИ ПММ в рамках изучения этой проблемы………………………………12

1.3. Обзор задач, связанных с процессами седиментации, барботажа, флотации, где важен учет «наследственной» силы Бассе……………………18

1.3.1. Седиментация ……………………………………………………………18

1.3.2. Аэрация(барботаж) или процесс насыщения кислородом воды………20

1.3.3. Флотация………………………………………………………………….22

2. Оценка влияния эффекта присоединенной массы на движение дисперсной фазы в поле сил тяжести……………………………………………………….32

3. Физико-математическая модель движения пузырька в вязкой жидкости с учетом присоединенной массы и силы Бассе………………………………...38

3.1. Физико-математическая модель движения пузырька в случае присутствия в жидкости поверхностно–активных веществ (ПАВ)……………………….38

3.2. Физико-математическая модель движения пузырька с учетом поправки Адамара–Рыбчинского ………………………………………………………..44

4. Результаты численного исследования, сравнение с экспериментом................................................................................................46

Выводы............................................................................................................57

Литература……………………………………………………………………...58

Приложение……………………………………………………………………..61

П.1. Программа расчета……………………………………………………….62

АННОТАЦИЯ

Особенности нестационарного движения частиц дисперсной смеси (твердых частиц, капель и пузырьков) в потоке жидкости или газа представляют интерес для решения ряда практических и технологических задач, связанных с обтеканием одиночной сферы бесконечным потоком. Понимание динамики и основных закономерностей движения частиц является важным в задачах экологии, в природных явлениях, в некоторых технологических процессах. В качестве примеров можно привести процессы седиментации, барботажа, флотации, качки судов и т.п. При нестационарном движении таких частиц начинают проявляться в полной мере эффект присоединенной массы и сила Бассе. Все существующие на данный момент работы в этой области посвящены исследованию течений при Re>1 (большие скорости частиц и малая вязкость жидкой среды). Данная работа восполняет этот пробел и рассматривает проблему при малых числах Рейнольдса (Re<1). Получено численное решение математической модели всплытия пузыря воздуха с учетом эффекта присоединенной массы и сила Басе на основе созданной программы расчета на алгоритмическом языке программирования Fortran. Работа выполнялась в тесном контакте с коллективом ученых НИИ ПММ, где были проведены экспериментальные исследования по этой проблеме.

СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ

Re – число Рейнольдса

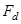- сила сопротивления

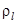- плотность дисперсионной среды

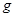- ускорение свободного падения

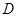- диаметр частицы

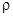- плотность материала частицы

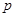- давление

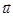- вектор скорости частицы

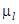- коэффициент динамической вязкости жидкости

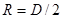- радиус шара (частицы)

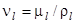- коэффициент кинематической вязкости дисперсионной среды

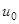- стационарная скорость движения частицы

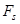- сила Стокса

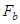- сила Бассе

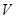- скорость несущей среды (жидкости)

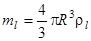- присоединенная масса жидкости

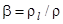- отношение плотности жидкости и частицы

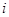- единичный вектор

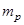- вес 100 частиц, в граммах

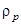- плотность частицы

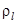- плотность раствора

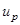- скорость стационарного осаждения частицы

r – радиус пузыря

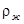- плотность жидкости

t – время

Введение

Закономерности движения частиц дисперсной смеси (твердых частиц, капель и пузырьков) в потоке жидкости или газа представляют интерес для решения ряда практических и технологических задач, связанных с обтеканием одиночной сферы бесконечным потоком. Понимание динамики и основных закономерностей движения частиц является важным в задачах экологии, в природных явлениях, в некоторых технологических процессах. В качестве примеров можно привести процессы седиментации, барботажа, флотации, очистка и прогнозирование распространения дымовых газов из труб промышленных предприятий и тепловых электростанций, предотвращение взрывов угольной пыли в шахтах, распространение облака жидко-капельного аэрозоля и т.д.

Интерес к данной проблеме связан также с экспериментальными и теоретическими трудностями моделирования движения двухфазной системы ввиду сложности регистрирования быстропротекающих процессов и малых значений динамических параметров, требующих использование чувствительных элементов, и корректного построения моделей с учетом нестационарных слагаемых в уравнении движения, соответственно.

Седиментация

Частицы дисперсной фазы одновременно испытывают действие силы земного притяжения и архимедовой силы; в зависимости от соотношения плотностей дисперсионной среды и дисперсной фазы равнодействующая этих сил будет вынуждать частицы к оседанию либо всплытию. Процесс оседания либо всплытия коллоидных частиц в золе называется седиментацией. Однако седиментации всегда противодействует другой процесс, стремящийся к равномерному распределению коллоидных частиц по всему объему раствора – диффузия, осуществляемая под действием броуновского движения частиц. Соотношение между этими двумя процессами определяет кинетическую устойчивость золей – способность коллоидных частиц удерживаться во взвешенном состоянии, не подвергаясь седиментации.

В статистической теории броуновского движения, развитой А. Эйнштейном, вводится понятие средний сдвиг ±Δx, представляющий собой проекцию расстояния между положениями частицы X1 и X2, в которых частица находилась во время двух последовательных наблюдений через время t. Значение квадрата среднего сдвига можно найти по уравнению Эйнштейна, связывающего Δx2 с температурой T, радиусом взвешенных частиц r и вязкостью среды η:

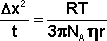
Средний сдвиг частицы связан с коэффициентом диффузии D, который может быть рассчитан по уравнению (IV.22):

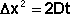
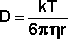
Как видно из уравнения (IV.23), величина коэффициента диффузии определяется отношением тепловой энергии молекул kT и вязкостного сопротивления диффузии со стороны среды. Поскольку процесс диффузии проявляется тем сильнее, чем меньше масса коллоидных частиц, более крупные частицы оседают либо всплывают в первую очередь. Кинетическая устойчивость золя, таким образом, прямо пропорциональна степени дисперсности золя. Заметное оседание частиц в системе, обладающей высокой кинетической устойчивостью, можно вызвать при помощи центрифугирования золя, используя значительные по величине центробежные силы, что многократно увеличивает силу, действующую на частицу и способствующую её оседанию (современные ультрацентрифуги работают при ускорениях свыше 400000g)

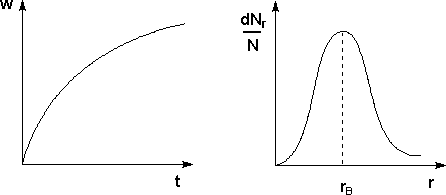
Рис. 4.15 Кривая седиментации Рис. 4.16 Кривая распределения

Методы седиментации и ультрацентрифугирования применяются для изучения полидисперсности коллоидных систем, обусловленной существованием в коллоидных системах частиц различных размеров. Изучение полидисперсности коллоидных систем для установления количественного распределения частиц по размерам (т.н. кривых распределения) – седиментационный анализ – производится при помощи измерения возрастания веса осевших частиц w со временем. По результатам такого исследования строят кривые седиментации (рис. 4.15). Проводя анализ кривой седиментации, можно рассчитать кривую распределения для данной системы, которая характеризует относительное содержание в системе частиц разного размера (рис. 4.16). Обычно кривые распределения содержат один максимум, который соответствует rв – наиболее вероятному радиусу частиц дисперсной фазы.

Флотация

Флотация является сложным физико-химическим процессом, который нашел широкое применение в обогащении полезных ископаемых.

Глубокие специальные теоретические изыскания в области флотационной очистки воды или сточных вод почти не проводились. Перенесение теоретических закономерностей флотационного процесса из практики обогащения в практику очистки сточных вод вполне допустимо, однако необходимо учитывать, во-первых, специфические особенности состава сточных вод, во-вторых, принципиально иные задачи, решаемые при очистке сточных вод. Если при обогащении решается задача отделения полезных минералов от пустой породы или разделения минералов, то при очистке сточных вод ставится задача наиболее полного удаления всех нерастворимых примесей и взвешенных веществ.

Извлечение тонкоизмельченных частиц из жидкости, в которой они находятся во взвешенном или коллоидальном состоянии, происходит в результате прилипания частиц к пузырькам газа (воздуха), образующимся в жидкости или введенным в нее (пенная флотация). Прикрепившиеся к пузырькам воздуха частицы всплывают на поверхность, образуя пенный слой с более высокой концентрацией частиц, чем в исходной жидкости.

Кроме того, в пенном продукте попутно наблюдается и повышение концентрации некоторых растворенных веществ и отдельных ионов. В особых случаях обработки сточных вод это может рассматриваться как самостоятельная задача, решаемая с помощью флотации.

Таким образом, при очистке сточных вод наряду с флотацией в сложной гетерогенной системе, т. е. системе, состоящей из двух или более фаз, может иметь значение и флотация в простой гетерогенной системе, состоящей из одной фазы. В первом случае из сточной жидкости будут удаляться главным образом нерастворенные частицы и коллоиды совместно с некоторым количеством растворенных высокомолекулярных соединений — поверхностно-активных веществ, во втором — только молекулы поверхностно-активных веществ (в основном высокомолекулярных) и некоторые ионы.

При сложном механико-химическом составе сточной жидкости в зависимости от соотношения концентраций нерастворенных и растворенных флотирующихся загрязнений, а также от того, какие загрязнения мы стремимся в данном случае выделить, можно представлять рассматриваемый процесс то как пенную флотацию, то как пенную сепарацию.

Требования к свойствам пенного слоя также несколько различны при обогащении и очистке сточных вод. Если при обогащении чрезмерная устойчивость пены нежелательна ввиду характера последующих операций над ней, то при очистке сточных вод желательно иметь более устойчивую пену, чтобы накапливая ее на поверхности получать шлам с меньшей влажностью. Вместе с тем пена должна прочно удерживать всплывающие частицы, не допуская их выпадения обратно в жидкость.

Флотационные процессы вообще определяются как процессы молекулярного прилипания частиц флотируемого материала к поверхности раздела двух фаз, чаще всего газа и воды, обусловленные избытком свободной энергии поверхностных пограничных слоев, а также особыми поверхностными явлениями смачивания, которые возникают в местах соприкосновения трех фаз (жидкость - газ — твердое тело), т. е. по периметру смачивания. Прилипание частицы, находящейся в жидкости, к поверхности газового пузырька возможно только тогда, когда имеет место не смачивание или плохое смачивание частицы данной жидкостью. Смачивающая способность жидкости зависит от ее полярности. С возрастанием полярности способность жидкости смачивать твердые тела уменьшается. Вода смачивает все тела, кроме некоторых «жирных» органических тел, аполярных по своей структуре. Внешним проявлением способности жидкости к смачиванию является величина поверхностного натяжения ее на границе с газом, а также разность полярностей на границе жидкость — твердое тело. Чем меньше поверхностное натяжение жидкости и разность полярностей, тем лучше тело смачивается ею.

Степень смачивания жидкостью твердой поверхности (при неполном смачивании) может быть выражена количественно величиной краевого угла смачивания, который принято отсчитывать в сторону жидкой фазы.

Этот угол замеряется нанесенной на сухую поверхность каплей воды или пузырьком воздуха, подведенным под помещенную в жидкость поверхность твердого тела. На степень смачивания (или иначе говоря, на силу прилипания пузырьков к частицам) оказывает влияние характер взаимодействия между частицей и водой, частицей и растворенным в воде кислородом. Взаимодействие с кислородом может привести к повышению смачиваемости за счет образования окислов, а с диполями воды приводит к образованию гидратной оболочки (толщиной до 0,1 мкм), что также повышает смачиваемость и препятствует закреплению пузырьков. Образование гидратных оболочек возможно в тех случаях, когда энергия связи между самими диполями воды меньше энергии связи между диполями воды и поверхностью твердой частицы. Очень тонкие гидратные оболочки (от 3 до 400 А) не препятствуют закреплению пузырьков.

Таким образом, смачивание определяется свойствами жидкости и зависит от свойств твердого тела. По отношению к воде твердые тела могут быть гидрофобными, гидрофильными или занимать какое-то промежуточное положение. К первым относятся вещества, имеющие аполярное строение молекул и в силу этого неспособные гидратироваться. Такие вещества обладают наименьшей смачиваемостью и поэтому легко флотируются. Чем меньше гидратирована частица, тем легче разрывается гидратная оболочка при приближении частицы к пузырьку газа (воздуха), и частица прилипает к пузырьку, поскольку такое состояние соответствует минимуму свободной энергии системы.

Гидрофильные вещества с полярным строением молекул в воде сильно гидратируются, а поэтому хорошо смачиваются водой и не могут флотироваться. Вещества с гетерополярным строением молекул (полярно-неполярные) способны гидратироваться со стороны полярной группы. В то же время со стороны углеводородной группы они являются гидрофобными и способны слипаться с пузырьками газа. В процессах флотации эти вещества играют особо важную роль.

Для получения флотационного эффекта в воде требуется предварительная гидрофобизация гидрофильных частиц. Достигается она путем ввода в жидкость поверхностно-активных реагентов-собирателей с полярно-неполярными молекулами, которые, адсорбируясь на поверхности гидрофильных частиц, ориентируются в адсорбционном слое неполярными углеводородными группами в окружающую среду, делая частицы гидрофобными н создавая тем самым необходимые условия для их флотации. Наиболее распространенные в практике флотации реагенты-собиратели могут быть разделены по природе солидофильных групп (групп, закрепляющихся на частичке) на несколько типов, отличающихся по своим флотационным свойствам:

Ø масла и смеси различных соединений, являющихся продуктами переработки нефти, угля, сланцев, дерева (нефть, керосин, мазут, смолы и др.);

Ø кислоты с углеводородными радикалами (жирные кислоты и их соли, олеат натрия, нафтеновые кислоты, олеиновая, стеариновая и пальмитиновая кислоты и др.);

Ø соединения, содержащие в полярной части двухвалентную серу (меркаптаны, ксантогенаты, дитиокарбонаты, тритиокарбонаты, дитиофосфаты и др.);

Ø соединения, содержащие в полярной части анион серной кислоты (алкилсульфаты, алкилсульфонаты и др.);

Ø соединения, содержащие в полярной группе азот или фосфор (амины, соли аммония, этаноамин, соли пиридина).

Повышение гидрофобности и флотируемости материала может осуществляться не только воздействием реагентов, но и некоторыми другими путями, например, сорбцией молекул растворенных газов на поверхности частичек. Такая сорбция должна в той или иной степени уменьшать общую гидратированность поверхности частичек. Однако вследствие того, что гидратная оболочка теряет свои растворяющие свойства и тем больше, чем сильней поляризация воды, диффузия молекул газов к поверхности гидратированной частицы затруднена. Исследования показывают, что активизирующее действие растворенных газов на флотацию наиболее заметно в присутствии реагентов-собирателей. Особую роль при этом играют пузырьки воздуха, выделяющиеся из раствора (при его пресыщении воздухом) на поверхности частички. Эти микропузырьки в какой-то степени дегидратируют ее, способствуя прилипанию более крупного пузырька и флотации частицы. При небольших размерах частицы могут флотироваться и за счет образовавшихся на них микропузырьков.

Теоретические и экспериментальные данные показывают, что пузырьки, возникающие из пресыщенного раствора, образуются мгновенно и преимущественно на подготовленных к флотации частицах, а не спонтанно, поскольку работа, затрачиваемая на образование спонтанного пузырька, больше затрачиваемой на образование такого же пузырька на твердой поверхности. Вероятность образования пузырька на поверхности частиц тем выше, чем лучше они подготовлены к флотации.

Пузырьки, образующиеся на твердой поверхности, тем мельче, чем больше пресыщен раствор воздухом. Вначале они достигают величины всего в несколько микрон, затем увеличиваются за счет коалесценции друг с другом или с пузырьками, возникшими спонтанно. Это имеет существенное значение при выборе способа флотации, указывая на определенные преимущества флотации при выделении воздуха из раствора.

В практике очистки сточных вод часто приходится иметь дело с флотацией хлопьев скоагулированных коллоидов, коагулянтов и гидроокисей металлов. Вероятность прилипания пузырьков газа к хлопьям и прочность сцепления их между собой тем выше, чем меньше времени прошло с момента образования хлопьев.

Наши наблюдения показывают, что «флотационная активность» хлопьев по мере их «старения» заметно падает, а спустя несколько часов они вовсе могут потерять способность флотироваться. Наилучшими с точки зрения флотации хлопьев коагулированных коллоидов и гидроокисей являются условия, когда процессы выделения пузырьков газа из раствора и образования хлопьев происходят одновременно, что имеет место, например, при электрокоагуляции — флотации.

Исследованиями установлено, что размер нужных для флотации пузырьков увеличивается с увеличением размера частиц при их одинаковой гидрофобности, т. е. прилипание частиц малого размера соответственно к пузырькам малого размера более вероятно. чем к пузырькам большого размера. В условиях пониженной гидрофобности вообще более вероятным будет прилипание мелких пузырьков. При увеличении размера частиц, а также при понижении их гидрофобности создаются условия, благоприятствующие образованию не минерализованных пузырьков, а аэрофлокул.

Большое значение для флотационного процесса имеет образование пузырьков определенной крупности и их сохранение (стабилизация). Последнее достигается путем ввода в жидкость реагентов-пенообразователей, повышающих дисперсность пузырьков и способствующих их устойчивости. Пенообразователи адсорбируются на поверхности раздела жидкость — газ, понижая поверхностное натяжение жидкости на нем. Полярная часть реагента-собирателя реагирует с молекулами воды, а аполярная часть ориентируется в газовую фазу.

Концентрируясь на поверхности раздела жидкость — газ, вспениватель уменьшает поверхностную энергию раздела фаз, способствуя тем самым, с одной стороны, стабилизации пузырьков, а с другой, — улучшая процесс прилипания к пузырькам твердых частиц.

К пенообразователям относятся сосновое масло (или тяжелый пиридин), креозол, ксиленол, фенолы и некоторые синтетические моющие вещества — алкилсульфонат, алкиларилсульфонат, алкилсульфат натрия (моющее средство «Прогресс») и др.

Многие флотореагенты, особенно синтетические, обладают и собирательными, и вспенивающими свойствами.

Имеется еще одна группа флотореагентов-регуляторов, активизирующих или подавляющих флотацию того или иного вещества (известь, сода, серная кислота, сернистый натрий, медный и цинковый купорос и др.). В практике очистки сточных вод их специальное применение (за исключением создания определенной рН среды, имеющей в ряде случаев значение для флотации) вряд ли может иметь место. Однако следует учитывать, что иногда возможно ухудшение эффекта флотации определенного ингредиента (загрязнения) в сточных водах из-за присутствия реагента-подавителя.

Процесс прилипания частиц загрязнения к пузырькам воздуха является основным актом флотации, а одной частицы к пузырьку — элементарным актом флотации.

Прилипание загрязнений к пузырькам происходит двумя путями: при столкновении частицы с пузырьком и при возникновении пузырька из раствора на поверхности частицы. На основании термодинамического и кинетического анализов процессов прилипания можно сделать выводы, что чем гидрофобнее поверхность частички, тем вероятнее ее прилипание к воздушному пузырьку при их столкновении; сила столкновения и время контакта могут быть тем меньше, чем гидрофобнее частица и чем гидрофобнее ее поверхность, тем вероятнее образование на ней пузырьков газов, выделяющихся из раствора.

Это еще раз подчеркивает необходимость тщательной подготовки (гидрофобизацпи) частиц загрязнений перед флотацией их.

При очистке сточных вод приходится иметь дело преимущественно с очень мелкими, шламовыми частицами. Для их флотации требуются очень мелкие воздушные пузырьки (размером в несколько микрон) и высокая степень насыщения ими сточных вод. При хорошей подготовке частиц к флотации (гидрофобизации) будет происходить флокуляция их путем сцепления аполярых групп реагентов, находящихся на поверхности частиц, флокуляция создает лучшие условия для флотации шламовых частиц. Для укрупнения частиц целесообразно применять коагуляцию, особенно в тех случаях, когда наряду с мелкими частицами надо сфлотировать и более крупные, флотация которых в присутствии шламов будет ухудшаться.

Создание во всем объеме жидкости, где взвешенные вещества находятся в мелкодисперсном состоянии, воздушной эмульсии является необходимым условием для успешного прилипания частиц к пузырькам воздуха. При этом значительный процент частичек флотируется за счет пузырьков воздуха, выделившихся непосредственно на их поверхности, остальные — посредством слипания с пузырьками воздуха, выделившимися или на поверхности других частичек, или спонтанно. В стесненном состоянии воздушно-водяной эмульсии этот процесс протекает весьма интенсивно.

Тонкие шламовые частицы, если они достаточно флотоактивны, покрывают тонким слоем поверхность воздушных пузырьков, образуя своеобразные шламовые зерна, более крупные к таким зернам прилипают плохо. Наружные обкладки пузырьков способствуют их устойчивости, прочности и продолжительности существования пенного слоя, что при очистке сточных вод имеет существенное значение, так как позволяет получать пенный продукт (шлам) с более низкой влажностью за счет накопления его в течение некоторого времени на поверхности жидкости.

Пены, получающиеся при флотации, могут иметь различное строение — агрегатное, пленочное или пленочно-структурное. При флотации сточных вод наиболее вероятно образование пленочно-структурных пен, которые содержат большое количество воды, особенно в нижних слоях, а устойчивость и подвижность их изменяется в зависимости от количества флотореагентов и характера загрязнений, выносимых в пенный слой.

При подъеме шламовых зерен в пенный слой начинаются процессы флокуляции, т. е. агрегирование отдельных минерализованных пузырьков в аэрофлокулы и их коалесценция, в результате чего образуются крупные шламовые агрегаты (диаметром 2—3 мм) из мелких пузырьков с налипшими на них частицами взвесей. Соприкасаясь вплотную своими наружными обкладками, агрегаты постепенно слипаются друг с другом, одновременно стремясь подняться вверх в силу своей плавучести. Находящаяся в просветах вода стекает вниз, уменьшая тем самым общую влажность шлама. Шлам после полного объединения зерен представляет собой одну сплошную массу с включенными в нее пузырьками воздуха или других газов. Через 5—10 ч накопления шлама содержание в нем твердого вещества увеличивается с 1—2% до 6—10%, пузырьки воздуха занимают 20—30% общего объема.

Следует отметить, что шлам по достижении им влажности около 90% в дальнейшем уплотняется и обезвоживается значительно медленнее, так как прослойки воды, заключенные между частицами, имеют толщину, исчисляемую несколькими микронами, и, как показали исследования, теряют обычные гидравлические свойства, что затрудняет стекание воды. Кроме того, в шламах сточных вод содержится значительный процент коллоидальных частиц, которые легко гидратируются, но воду отдают плохо.

На устойчивость пен влияют молекулы реагентов-пенообразователей и частицы флотируемых материалов. Наилучшим образом стабилизируют пену поверхностно-активные вещества, образующие в воде коллоидные и полуколлоидные растворы (сапонин, и др.).

Реагенты, образующие истинные растворы (низшие спирты, скипидары и др.), и те, которые практически нерастворимы в воде (веросин и др.), при больших дозах резко уменьшают устойчивость пен.

Стабилизирующее действие сфлотированных частиц тем выше, чем более они гидрофобны, мельче и чем больше их форма приближается к плоской, чешуйчатой. Присутствие реагента, уменьшающего силу прилипания частиц к пузырькам, будет отрицательно сказываться и на устойчивости пены.

Таким образом, кинетику флотационного процесса характеризуют следующие факторы:

ñсила прилипания пузырька к частице, определяемая величиной краевого угла и размерами пузырька;

ñкинетика разрыва промежуточной жидкой прослойки, приводящей к образованию тонкой пленки, отличной по своим свойствам от жидкости в объеме;

ñразмер частиц;

ñсорбция газов на поверхности частиц и химическое взаимодействие газов (в частности, кислорода) с частицами;

ñизменение величины краевого угла с течением времени;

ñвлияние реагентов на величину краевого угла и на устойчивость пузырьков и флотационных пен;

ñусловия зарождения и образования пузырьков на границе раздела жидкость — твердое тело за счет выделения растворенных газов;

ñмеханизм минерализации пузырьков в загрязненной воде и пенном сл

Физико-математическая модель движения пузырька в случае присутствия в жидкости поверхностно–активных веществ (ПАВ)

В отличие от известных работ, посвященных данной проблеме, обзор которых приведен во введении, мы исследуем режим движения пузырька при малых числах Рейнольдса (Re<1).

Математическая модель строится при следующих допущениях:

1. Число Рейнольдса Re<1

2. В жидкости имеются поверхносно–активные вещества (ПАВ), которые препятствуют движению жидкости на поверхности пузыря. Поэтому обтекание пузыря происходит также, как и обтекание твердого шарика.

Введем обозначения:

r – радиус пузыря; 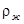- плотность жидкости; 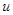- скорость пузыря; t – время; 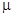- коэффициент динамической вязкости; g – ускорение силы тяжести.

На пузырь действуют силы:

1. инерции 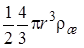(масса газа в пузыре мала по сравнению с присоединенной массой жидкости).

2. вязкого сопротивления - .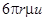

3. ускорение силы тяжести 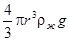- сила Архимеда.

4. сила Бассэ 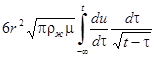[30].

Приравнивая эти силы, получаем уравнения движения пузыря (далее )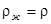

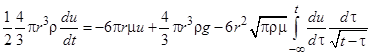. (1)

Поделим это уравнение на присоединенную массу жидкости 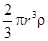. Получаем

.

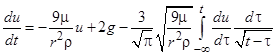Введем характерное время 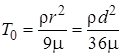и безразмерное время 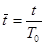. Получим

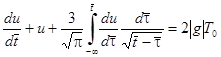, где g<0.

В дальнейшем будем предполагать, что при 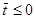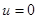[30]. Фактически это означает, что при 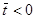пузырек неподвижно закреплен. При этом предположении уравнения движения принимают вид:

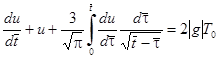. (2)

Так как 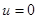при 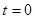, второе слагаемое в левой части можно представить в виде 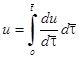и записать уравнение в форме

.

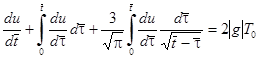Для ускорения пузыря введем обозначение 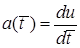и получим уравнение

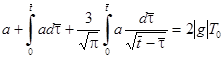. (3)

Последнее уравнение решено операционным методом И.М. Васениным [29]. Полагаем 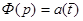. При переходе к изображениям воспользуемся теоремой об интегрировании оригинала, согласно которой 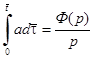и теоремой умножения Бореля

.

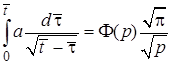(См. [30]).

В результате перехода к изображениям из (3) получим

.

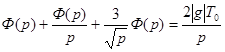Отсюда выражаем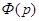

.

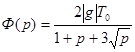С целью нахождения оригинала представим эту формулу в виде

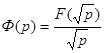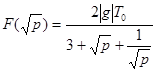, где . (4)

Согласно [30] оригинал 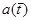равен

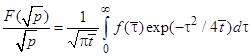, (5)

где .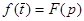

В нашем случае 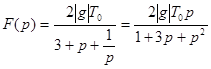и оригинал можно вычислить по второй теореме разложения, согласно которой 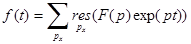, где вычеты берутся по особым точкам функции 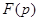[30].

Полагая 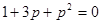находим особые точк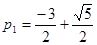и и 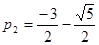. Каждая из этих точек представляет собой полюс первого порядка, а функция 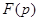является дробно-рациональной функцией вида .

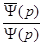Для таких функций 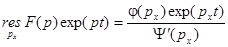[30].

Используя эту формулу, находим

,

.

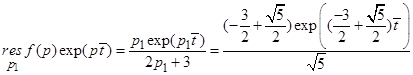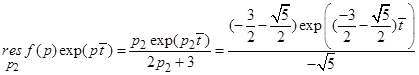Подставляя сумму вычетов в формулу (5) получим

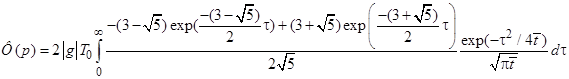(6)

Преобразуем каждый из двух интегралов, входящих в (6)

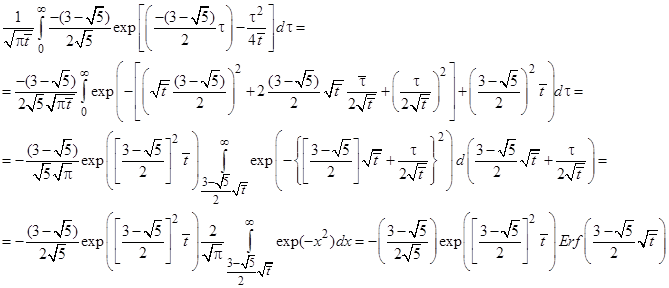Аналогично найдем

.

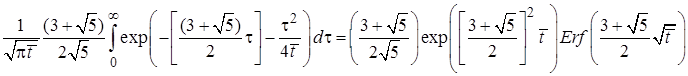Таким образом,

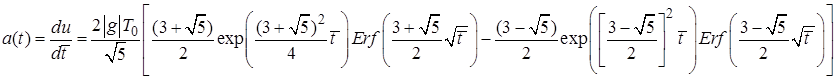(7)

Интегрируя по 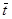с начальными условиями 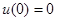получим

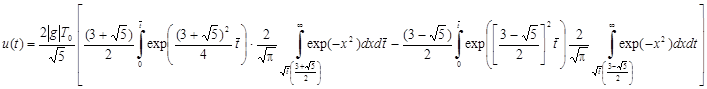(8)

Интегралы вычисляем по частям

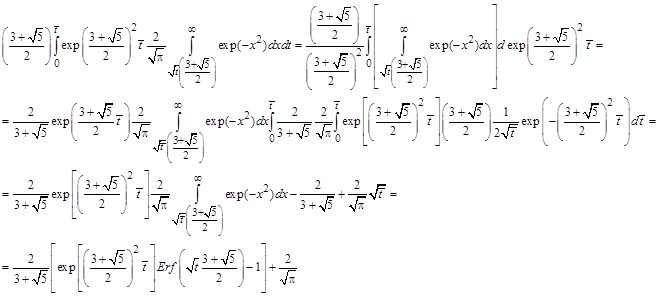Аналогично

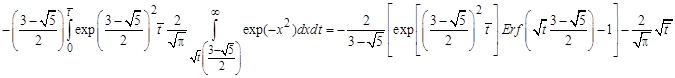
Подставляя интеграл в (8) после приведения подобных найдем

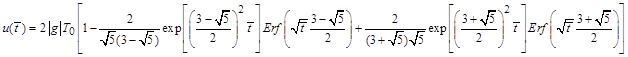
Проверка:

При 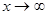, 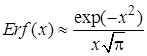и поэтому при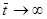

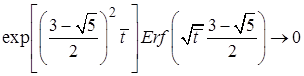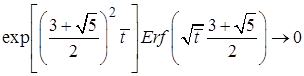, , соответственно,

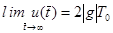. Последний результат есть решение уравнения (8) при 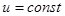, что соответствует выходу на стационарную скорость подъема пузырька.

Выводы

1. Создана программа расчета скорости и высоты всплытия пузыря с учетом силы Бассе и эффекта присоединенной массы при Re<1 на алгоритмическом языке Fortran.

2. Сравнение с результатами эксперимента показало хорошее совпадение расчетных и опытных данных.

3. Численные исследования, проведенные по этой программе, позволили грамотно спланировать условия эксперимента.

4. Полученные результаты показывают важность учета силы Бассе и эффекта присоединенной массы в нестационарных процессах.

Литература

1. Clift R., Grase J.R., Weber M.E. Bubbles, drops and particles. New York : Academic Press. 1978. 369 р.

2. Нигматулин Р.И.

3. Basset A.B. Treatise on hydrodynamics. London: Deighton Bell, 1888. Vol. 2. Chap. 22. P. 285-297.

4. Boussinesq J. Theorie Analytique de la chaleur. Paris, 1903. Vol.2. 224 p.

5. Oseen C.W. Hydrodynamik. Leipzig, 1927. 132 p.

6. Soo S.L. Fluid dynamics of multiphase systems. Braisdell, Waltham, MA, 1967.

7. M.X. Maxey, J.J. Riley. Equation of motion for small rigid sphere in a nonuniform flow // Phys. Fluids. 1983. №26. P. 883-889.

8. Michaelides E.E.A novel way of computing the Basset term in unsteady multiphase flow computations // Physics of fluids, A1. 1992. V. 4, № 7.Р. 1579-1582.

9. Невский Ю.А., Осипцов А.Н. О роли нестационарных и «наследственных» сил в задачах гравитационной конвекции суспензий // Вестник Московского университета. Серия 1. Математика. Механика. 2008. № 4. С. 37-40.

10. Dorgan A.J., Loth E. Efficient calculation of the history force at finite Reynolds numbers // International Journal of Multiphase Flow. 2007. Vol. 33. P.833-848.

11. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.6. Гидродинамика. М.:Наука, 1986. 736 с.

12. Ramarao B.V., Tien Chi. Role of Basset force on particle deposition in stagnation flow // J. Aerosol Sci. Vol.21, № 5. Р. 597-611.

13. A.S. Sangani, D.Z. Zhang, A. Prosperetti. The added mass, Basset, and viscous drag coefficients in nondilute bubbly liquids undergoing smallamplitude oscillatory motion // Phys. Fluids A 3 (12). 1991. P.2955-2970.

14. Thomas P.J. On the influence of the Basset history on the motion of a particle through a fluid // Physics of fluids А4. 1992. Р.2090-2093.

15. Druzhinin O.A., Ostrovsky L.A. The influence of Basset force on particle dynamics in two-dimensional flows // Physica D. 1994. № 76. P. 34-43.

16. Mordant N., Pinton J.-F. Velocity measurement of a settling sphere // The European Physical Journal B. 2000. № 18. P.343-352.

17. Jian Zhang, Liang-Shih Fan. On the rise velocity of an interactive bubble in liquids // Chemical Engineering Journal. 2003. Vol. 92. P. 169-176.

18. Mustapha Abbad, Mohamed Souhar. Effects of the history force on an oscillating rigid sphere at low Reynolds number // Experiments in Fluids. 2004. № 36. Р. 775-782.

19. Sobral Y.D., Olivera T.F., Cunha F.R. On the unsteady forces during the motion of a sedimenting particle // Powder Technology, 2007. V. 178,

Наши рекомендации