Экспериментальная оценка возможности обменных соотношений между характеристиками изображения
Для оценки возможности обменных соотношений между качественными характеристиками изображения целесообразно использовать психофизические квалиметрические экспертизы, основанные на моделировании значений оцениваемых характеристик, подобные экспертизам по экспериментальной оценке коэффициентов чувствительности к параметрам, однако в данном случае предполагается последующий расчет парных коэффициентов корреляции между параметрами.
Экспертам в последовательности, соответствующей последовательности случайных чисел, также, как и при экспериментальной оценке коэффициентов чувствительности, предъявляли изображения с измененным и неизменным значением характеристики. Причем, одинаковые процедуры и с одинаковой величиной ухудшения характеристики использовались для оценки заметности изменений характеристики как на тест- объекте, содержащем только информацию об исследуемом параметре, так и на сюжете. Оцениваемое изображение содержало два поля, одно являлось эталонным, а по второе поле вносились (или нет) изменения в анализируемую характеристику. Коэффициент чувствительности рассчитывался как 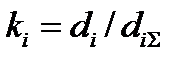 , где
, где 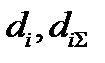 - статистические параметры (называемые также мерами обнаружимости сигнала), зависящие от вероятностей правильного обнаружения и ложных тревог соответственно для тест- объекта и сюжета при одинаковом изменении моделирующего параметра, влияющего на оцениваемую характеристику [9-10].
- статистические параметры (называемые также мерами обнаружимости сигнала), зависящие от вероятностей правильного обнаружения и ложных тревог соответственно для тест- объекта и сюжета при одинаковом изменении моделирующего параметра, влияющего на оцениваемую характеристику [9-10].
Теснота взаимосвязи между характеристиками оценивалась парными коэффициентами корреляции
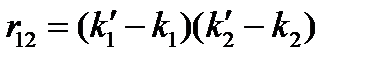 ;
;
Где 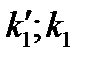 - коэффициенты чувствительности к яркости, причем,
- коэффициенты чувствительности к яркости, причем, 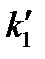 определялся при ухудшении детальности;
определялся при ухудшении детальности; 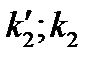 коэффициенты чувствительности к детальности, причем
коэффициенты чувствительности к детальности, причем 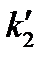 определялся при ухудшении яркости.
определялся при ухудшении яркости.
Анализ результатов экспериментальных исследований показывает, что между яркостью и четкостью изображения существует линейная корреляция, при этом парный коэффициент корреляции между коэффициентами чувствительности к этим характеристикам составляет 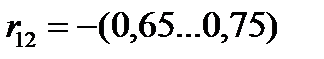 (для условий рассматривания видеоизображения в учебной лаборатории при величине вероятности ложных тревог, не превышающей 0,20). Величина коэффициента указывает на тесное взаимное влияние исследуемых параметров.
(для условий рассматривания видеоизображения в учебной лаборатории при величине вероятности ложных тревог, не превышающей 0,20). Величина коэффициента указывает на тесное взаимное влияние исследуемых параметров.
Отрицательное значение коэффициента корреляции объясняется тем, что если при ухудшении яркости коэффициент чувствительности к детальности уменьшается, то в свою очередь при ухудшении детальности коэффициент чувствительности к субъективно воспринимаемой яркости возрастает.
Для того чтобы убедиться, что корреляционная зависимость действительно является значимой, следует использовать проверку гипотезы о значимости линейной статистической связи. Такая проверка заключается в определении минимального значения коэффициента корреляции, отклонение которого от нуля можно считать значимым.
Алгоритм проверки данной гипотезы включает определенные этапы:
- выдвигаются две гипотезы:
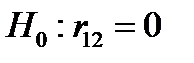 ;
; 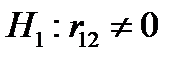 ;
;
- принимается уровень значимости: в дальнейших расчетах принят уровень значимости 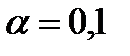 , такая величина соответствует доверительному интервалу, в котором лежат субъективные оценки при квалиметрических экспертизах;
, такая величина соответствует доверительному интервалу, в котором лежат субъективные оценки при квалиметрических экспертизах;
- выбирается критическая граница (критическая статистика). Наиболее часто используемой является критическая статистика вида
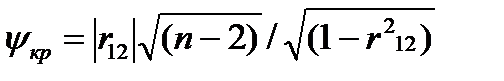 ,
,
где 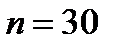 - объем экспериментальной выборки; величина критической статистики составила
- объем экспериментальной выборки; величина критической статистики составила 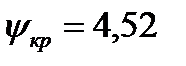 ;
;
- рассчитываются критические границы, в которых должна лежать величина 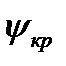 для того, чтобы выполнялась гипотеза
для того, чтобы выполнялась гипотеза 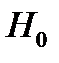 .
.
Верхняя критическая граница 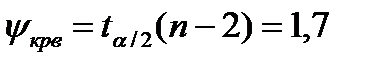 и нижняя граница
и нижняя граница 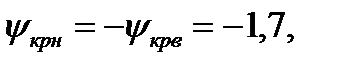 где
где 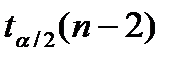 соответствуют t- распределению Стьюдента уровня
соответствуют t- распределению Стьюдента уровня 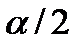 (Приложение 1).
(Приложение 1).
Как видно из результатов расчета, гипотеза 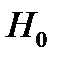 опровергается c ошибкой первого рода
опровергается c ошибкой первого рода 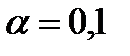 , корреляционная связь между коэффициентами чувствительности к яркости и четкости изображения с парным коэффициентом корреляции
, корреляционная связь между коэффициентами чувствительности к яркости и четкости изображения с парным коэффициентом корреляции 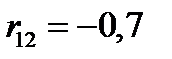 является значимой.
является значимой.
В то же время величины парных коэффициентов корреляции между коэффициентами чувствительности к яркости и геометрическим искажениям ( 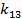 ) коэффициентами чувствительности к детальности и геометрическим искажениям (
) коэффициентами чувствительности к детальности и геометрическим искажениям ( 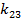 ) оказались ничтожными, что свидетельствует об отсутствии линейной корреляции и невозможности компенсации одного параметра другим.
) оказались ничтожными, что свидетельствует об отсутствии линейной корреляции и невозможности компенсации одного параметра другим.
Однако при этом может иметь место нелинейная зависимость между параметрами, при которой коэффициент корреляции теряет смысл характеристики степени тесноты связи, в этом случае используют такой критерий, как корреляционное соотношение

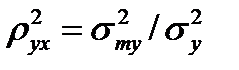
 ,
,
где 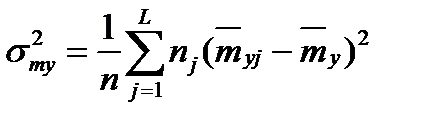 - дисперсия по интервалам, на которые разбит диапазон значений переменной x при обработке результатов;
- дисперсия по интервалам, на которые разбит диапазон значений переменной x при обработке результатов; 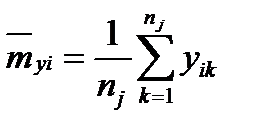 - частное математическое ожидание в j-м интервале,
- частное математическое ожидание в j-м интервале, 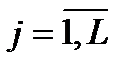 - номер интервала;
- номер интервала; 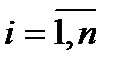 - количество экспериментальных результатов;
- количество экспериментальных результатов; 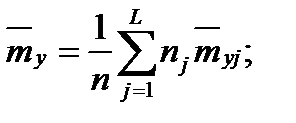
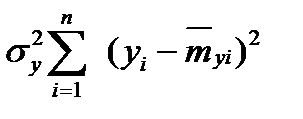 - общая дисперсия по всем экспериментальным результатам.
- общая дисперсия по всем экспериментальным результатам.
Проверка гипотезы об отсутствии или наличии нелинейной корреляционной связи заключается в нахождении величины корреляционного отношения, отличающегося от нуля на величину, при которой становится справедливой одна из двух гипотез:
- 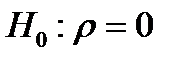 ;
;
- 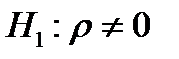 .
.
Уровень значимости в дальнейших расчетах принят равным 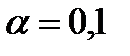 .
.
Величина критической статистики рассчитывалась как 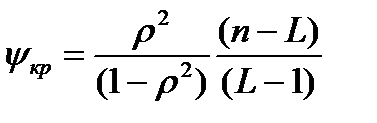 .
.
Гипотеза 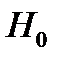 верна в том случае, если
верна в том случае, если 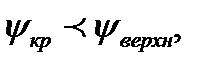 , где
, где 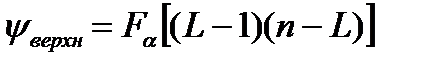 - табличная величина критерия Фишера (Приложение 2).
- табличная величина критерия Фишера (Приложение 2).
Результаты проверки гипотезы об отсутствии нелинейной корреляционной связи между коэффициентами весомости на примере технических параметров, определяющих качество киноизображения, приведены в Таблице 1. Таким образом, гипотеза 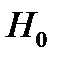 верна, для всех параметров, влияющих на качество киноизображения, нелинейная корреляционная зависимость оказалась незначимой. Что подтверждает отсутствие возможности обменных соотношений между анализируемыми характеристиками киноизображения, т.е. на невозможность компенсации ухудшения одного параметра повышением другого.
верна, для всех параметров, влияющих на качество киноизображения, нелинейная корреляционная зависимость оказалась незначимой. Что подтверждает отсутствие возможности обменных соотношений между анализируемыми характеристиками киноизображения, т.е. на невозможность компенсации ухудшения одного параметра повышением другого.
Таблица 1.
Результаты расчетов по гипотезы об отсутствии нелинейной взаимосвязи между характеристиками
| Название характеристик изображения, для которых определялись парные коэффициенты корреляции | Корреляционное отношение, ρ | Расчетное значение критической статистики, 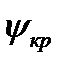 | Граничное значение статистики, 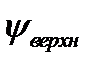 |
| Яркость – геометрические искажения | 0,000 | 0,000 | 2,5 |
| Детальность – геометрические искажения | 0,009 | 0,000 | 2,5 |
