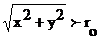Точечный источник круглой формы и постоянной яркости.
Распределение яркости описывается функцией
|
Функция L (x,y) представляет собой цилиндр, для нахождения пространственно- частотного спектра целесообразно применить преобразование Ганкеля.
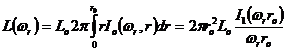 , (1)
, (1)
где 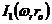 - функция Бесселя первого рода, первого порядка.
- функция Бесселя первого рода, первого порядка.
|
x = ρcosα, y = ρsinα.
Пространственно - частотный спектр выражается формулой (1). Этот спектр имеет все частоты до 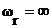 . Однако большая часть энергии сосредоточена на частотах
. Однако большая часть энергии сосредоточена на частотах 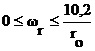 .
.
Для определения формы распределения по окружности необходимо найти спектр Фурье по углу 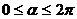 :
:
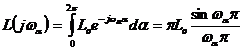 . (2)
. (2)
Этот спектр равен нулю в точках 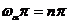 (n = 1, 2, …).
(n = 1, 2, …).
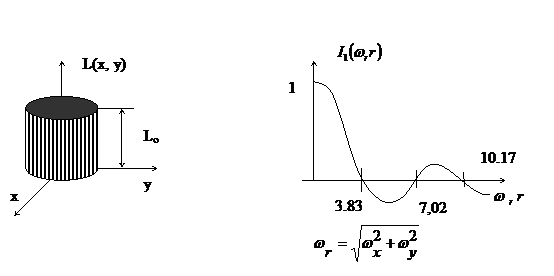
Рис.2. Точечный источник круглой форма постоянной яркости
Излучатель в виде отрезка идеальной прямой линии постоянной яркости.
Распределение яркости имеет вид:
|
Применив преобразование Фурье, получим
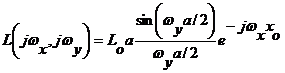 .
.
Модуль этого спектра равен:
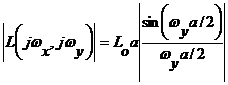
имеет максимальное значение 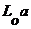 при
при 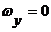 и
и 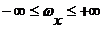 .
.
При значениях 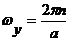 модуль равен «0».
модуль равен «0».
Отрезок прямой линии конечной ширины постоянной яркости.
Функция такой линии имеет вид:
|
a и b – протяженность источника излучения вдоль осей x и y.
Пространственно- частотный спектр описывается:
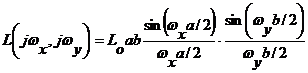 .
.
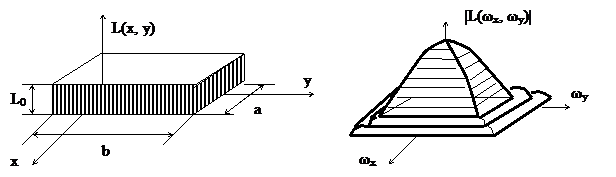 |
Рис.3. Излучатель в виде отрезка прямой линии и его спектр
Структура поля излучения
Предположим, что пространство поля излучения некогерентное. Интенсивность поля характеризуется яркостью L.
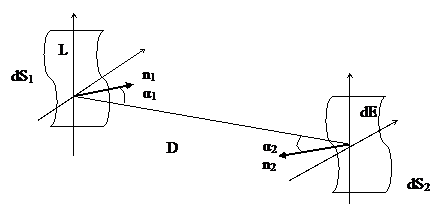
Рис.1.
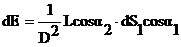 ,
,
где 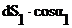 - эффективная площадь элементарной площадки в направлении приемной площадки.
- эффективная площадь элементарной площадки в направлении приемной площадки.
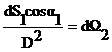 - элементарный пространственный угол, под которым видна излучающая площадка из точки приема.
- элементарный пространственный угол, под которым видна излучающая площадка из точки приема.
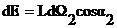
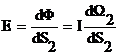
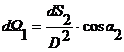
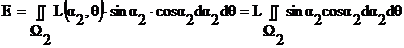
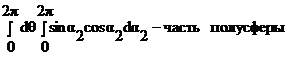
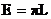 [Вт/м2 = Вт/м2 стр]
[Вт/м2 = Вт/м2 стр]
Пространство предметов является трехмерным. Источник излучения характеризуется двухмерной яркостью L (x,y).
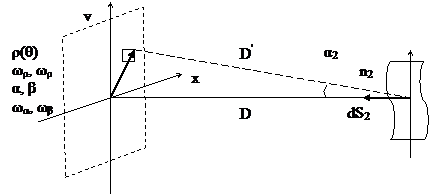 |
Рис. 2. Некоторая поверхность
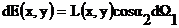 ,
,
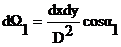 ,
,
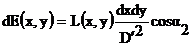 ,
,
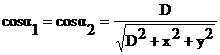 ,
,
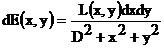 ,
,
Если х<<D, y<<D, то
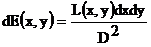 .
.
Функция L (x,y) полностью характеризует структуру поля в пространстве предметов в статике.
Сигналы могут быть многомерными, 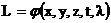 - яркость зависит от времени и длины волны.
- яркость зависит от времени и длины волны.
В общем случае ее можно представить в виде L= L (qm), где qm - многомерный вектор.
Если функция детерминирована и представляет собой частную реализацию случайного распределения яркости по поверхности, то такую функцию можно представить в виде преобразования Фурье, по каждому из параметров.
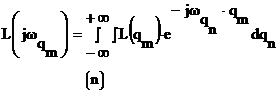 - элементарный интеграл,
- элементарный интеграл,
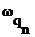 - пространственная частота элементарного вектора;
- пространственная частота элементарного вектора;
n - элементарный вектор в пространстве частот 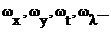
Первая гармоника: 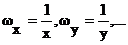 ;
;
n – я гармоника: 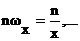 ;
;
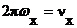 - циклическая и круговая частоты.
- циклическая и круговая частоты.
Условие периодичности:
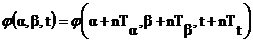
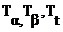 - отражают период повторения сигнала по данному параметру.
- отражают период повторения сигнала по данному параметру.
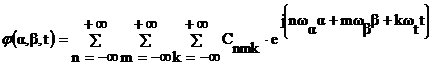 ,
,
где 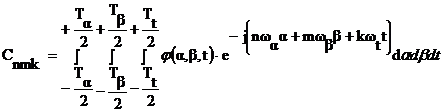 .
.
Так как функция периодична, то 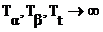 , что приведет к
, что приведет к
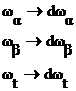
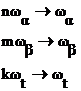
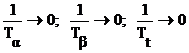 .
.
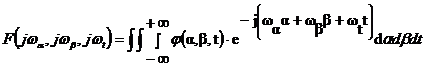
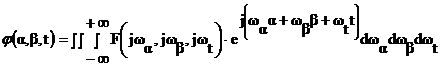
Если известно пространственное распределение яркости по поверхности объекта, можно определить функцию по параметру энергии.
Тема 19. Реакция оптической системы на входное воздействие.Освещенность плоскости изображения оптической системы. Влияние аберраций на распределение освещенности в изображении точечного источника, понятие о функции рассеяния, ее свойства.

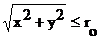 L(x, y)={ 0 при
L(x, y)={ 0 при