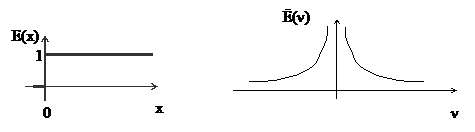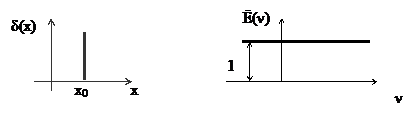Спектр непериодических сигналов

Предположим, что сигнал задан в виде функции времени, удовлетворяющей условию Дирихле и абсолютной интегрируемости, то есть при t ®µ u(t) ®0, а , действующей в пределах интервала t₁<t<t₂ .

Превратим u(t) в периодическую функцию u₁(t) с произвольным периодом T>(t₂-t₁) и, применив к ней разложение в ряд Фурье, запишем

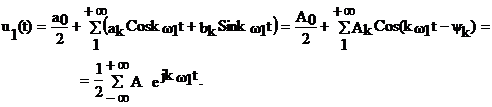(9) из принятых условий следует, что при T®µ u₁(t) ® u(t), а число гармонических составляющих растет, так как f₁=(1/T)=(w₁/2π) ® 0 , и, следовательно, расстояние между гармониками стремится к df, а спектр в силу этого становится сплошным и u₁(t) можно переписать в виде

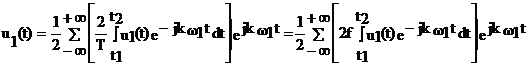а так как при T®µ 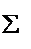переходит в 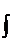, f₁ в df , а kw₁ в w, то

окончательно полученное соотношение представим в виде

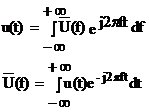(10)

Эти соотношения называют обратным и прямым преобразованием Фурье, соответственно. Физически они означают, что если известно спектральное распределение энергии сигнала, то временная форма сигнала может быть получена, если воспользоваться обратным преобразованием Фурье. Если же задана временная форма сигнала, то распределение его энергии по спектру определяется формулой прямого преобразования. Обычно 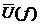называют спектральной плотностью или комплексным спектром Фурье сигнала u(t). Так как 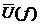df = 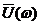dw, то 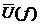=2π .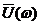

Для комплексного спектра, также как и для любой комплексной величины справедливы соотношения

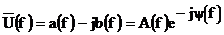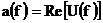, где , а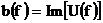

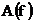- называют спектром амплитуд, а 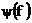- называют спектром фаз.

Спектр одиночного импульса

Предположим, что одиночный импульс задан в виде распределения освещенности E(x) некоторой поверхности q . Аналитически такой сигнал представляется функцией

E₀ êx ê £a/2 , êy ê£b/2

E(x) = í (11)

0 êx ê >a/2 , êy ê>b/2

Используя соотношение (10), найдем формулу, описывающую характер распределение спектра сигнала (11).

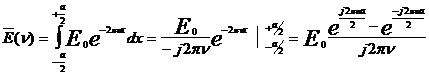, так как

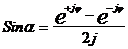, то, введя замену, окончательно получим

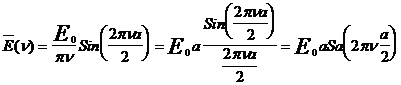, (12)

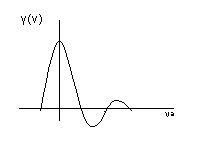
где использована замена [Sinx/x]= Sa(x). Проведя нормировку полученной функции на максимальное значение (E₀a =`E₀), получим функцию вида 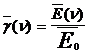, график которой показана на рис. .3.

Рис.3. Спектр одиночного импульса

Функция принимает нулевые значения в точках (πnа=nπ) ,то есть при n=n/а.

В области положительных значений 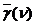имеет место равенство нулю начальных фаз всех гармонических составляющих. В области отрицательных значений 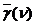начальные фазы меняют свои значения скачком на величину . Из графика спектрального распределения 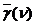освещенности сигнала E(x) видно, что при увеличении длительности а, она сдвигается в область низких частот, то есть спектр сигнала сужается, а при уменьшении длительности сигнала, спектр его становится более широкополосным.

Единичный скачок

Предположим, что сигнал задан в виде функции вида

1 x³0

E(x) ={ ,

0 x<0

которую называют единичным скачком. Для такой функции условие абсолютной интегрируемости не выполняется, так как 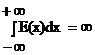и преобразования Фурье не могут быть применены непосредственно. Обойти эти затруднения можно, если рассмотреть функцию вида 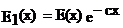, удовлетворяющую условиям абсолютной интегрируемости. Применив к ней прямое преобразование Фурье, получим:

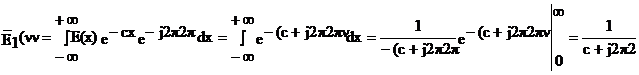если устремить с к нулю, то E₁(x) - к E(x) , поэтому 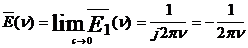, но так как -j= 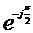, то

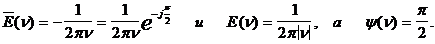(13)

Таким образом, спектральная плотность сигнала в виде единичного скачка обратно пропорциональна частоте, а фаза гармонических составляющих постоянна и равна p/2.

Рис.4. Единичный скачок

Единичный импульс

Функцию, показанную на рисунке 5 называют единичным скачком, функцией Дирака, дельта-функция. Особенностью функций такого вида является то, что она присутствует только в точке x=x₀ и за пределами этой точки ее значения равны нулю. Основными свойствами d(x) функции являются ее четность d(x)= d(-x) и то, что

.

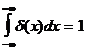Для нахождения спектра такой функции представим ее симметричной относительно точки x = x₀ с конечной длительностью D. Для такого сигнала спектральная плотность описывается выражением (12) и принимает вид 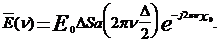Если D ®0 , а E(x) ®¥, то 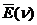®d(n) и

d(n)= 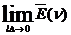, это означает, что d(n)= 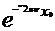, а модуль d(n)=A(n)=1.

Таким образом, спектр дельта-функции является сплошным в пределах от -¥ до +¥, а фаза гармоник равна 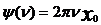, то есть все гармоники суммируются с одинаковыми начальными фазами.

Другим очень важным свойством дельта-функции является ее фильтрующее свойство, которое состоит в том, что

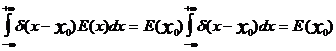(14)

так как 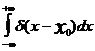=1.

Рис.5. Единичный импульс