Анализ, формальная постановка и выбор метода решения

На данном этапе по результатам анализа условия задачи выбирают математические абстракции, адекватно, т.е. с требуемой точностью и полнотой, представляющие исходные данные и результаты, строят модель задачи иопределяют метод преобразования исходных данных в результат (метод решения задачи).

Пример 1.1.Разработать программу, которая по заданным длинам сторон прямоугольника определяет его площадь.

Исходными данными в этом случае являются длины сторон прямоугольника, т.е. некоторые числовые значения, для которых должны быть заданы диапазон изменения и точность. Математические абстракции для представления исходных данных - некие изменяемые значения - переменные. Результат - площадь прямоугольника - также некоторое числовое значение, диапазон возможных значений и точность которого зависят от соответствующих характеристик исходных данных. Математической абстракцией результата также является переменная. Модель задачи можно представить в виде:

S=а´b,

где S - площадь; а, b - длины сторон.

Результат получают перемножением аргументов.

Однако полученная модель не является полной и, следовательно, адекватной, так как в ней не определены типы используемых переменных (целые или вещественные), что может привести к получению неверных результатов.

Например, допустим, что нас интересует площадь с точностью «до сотых», тогда получение результата с точностью «до целых» следует считать ошибкой.

Полная модель должна включать также указание типов переменных.

Часто формальная постановка задачи однозначно определяет метод ее решения. В тех случаях, когда задача может быть решена несколькими методами, выбирается один из них с учетом сложности и эффективности его реализации, обеспечиваемой методом точности результата, а также других параметров и характеристик.

При использовании процедурного подхода сложные задачи в процессе анализа разбивают на подзадачи, для каждой из которых может строиться своя модель и выбираться свой метод решения. При этом результаты решения одной подзадачи могут использоваться в качестве исходных данных в другой.

Определив методы решения, следует для некоторых вариантов исходных данных вручную или на калькуляторе подсчитать ожидаемые результаты.

Эти данные в дальнейшем будут использованы при тестировании программы.

Кроме того, выполнение операций вручную позволяет точно уяснить последовательность действий, что упростит разработку алгоритмов.

Целесообразно также продумать, для каких сочетаний исходных данных результат не существует или не может быть получен данным методом, что тоже необходимо учесть при разработке программы.

Проектирование

Принято различать логическое и физическое проектирование. Логическое проектирование не учитывает особенностей среды, в которой будет выполняться программа (технические и программные средства компьютера).

При выполнении физического проектирования все эти параметры должны быть учтены.

Логическое проектирование.Логическое проектирование при процедурном подходе предполагает детальную проработку последовательности действий будущей программы. Его начинают с определения структуры будущего программного продукта: отдельная программа или программная система, состоящая из нескольких взаимосвязанных программ. Затем переходят к разработке алгоритмов программ.

Алгоритмом называют формально описанную последовательность действий, которые необходимо выполнить для получения требуемого результата.

Различают последовательности действий (вычислений) линейной, разветвленной и циклической структуры.

Линейная структура процесса вычислений предполагает, что для получения результата необходимо выполнить некоторые операции в определенной последовательности. Например, для определения площади треугольника по формуле Герона необходимо сначала определить полупериметр треугольника, а затем по формуле его площадь.

Разветвленная структура процесса вычислений предполагает, что конкретная последовательность операций зависит от значений одного или нескольких параметров. Например, если дискриминант квадратного уравнения не отрицателен, то уравнение имеет два корня, а если отрицателен, то действительных корней нет.

Циклическая структура процесса вычислений предполагает, что для получения результата некоторые действия необходимо выполнить несколько раз. Например, для того, чтобы получить таблицу значений функции на заданном интервале изменения аргумента с заданным шагом, необходимо соответствующее количество раз определить следующее значение аргумента и посчитать для него значение функции.

Процессы вычислений циклической структуры в свою очередь можно разделить на три группы:

• циклические процессы, для которых количество повторений известно - счетные циклы или циклы с заданным количеством повторений;

• циклические процессы, завершающиеся по достижении или нарушении некоторых условий - итерационные циклы;

• циклические процессы, из которых возможны два варианта выхода: выход по завершении процесса и досрочный выход по какому-либо дополнительному условию - поисковые циклы.

Формальное описание алгоритмов осуществляют с использованием схем алгоритмов и псевдокодов.

На изображение схем алгоритмов существует ГОСТ 19.701-90, согласно которому каждой группе действий ставится в соответствие блок особой формы.

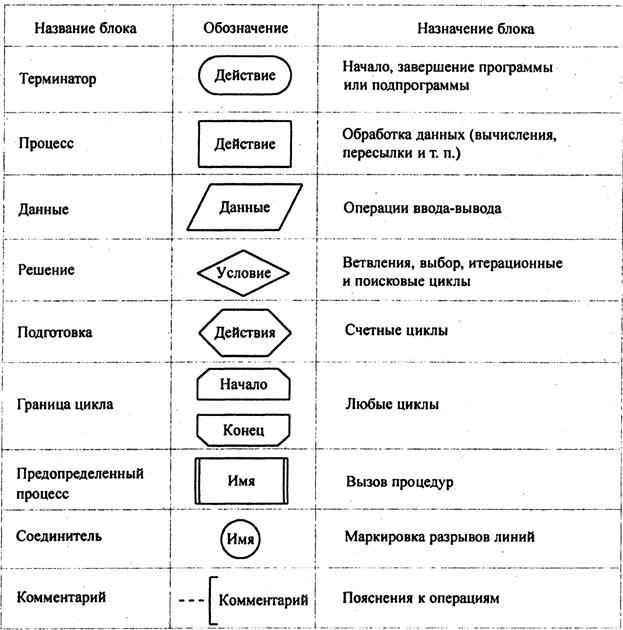
Некоторые часто используемые обозначения приведены в табл. 1.1.

При разработке алгоритма каждое действие обозначают соответствующим блоком, показывая их последовательность линиями со стрелками на конце. Для простоты чтения схемы желательно, чтобы линия входила в блок сверху, а выходила снизу. Если линии идут не слева направо и не сверху вниз, то стрелка в конце линии обязательна, в противном случае ее можно не ставить.

В случае, когда схема алгоритма не умещается на листе, используют соединители.

При переходе на другой лист или получении управления с другого листа в комментарии указывается номер листа, например «с листа 3» «на лист 1».

В теории программирования доказано, что для записи любого сколь угодно сложного алгоритма достаточно трех базовых структур:

• следование - обозначает последовательное выполнение действий (рис. 1.2, а);

• ветвление - соответствует выбору одного из двух вариантов действий (рис. 1.2, б);

• цикл-пока - определяет повторение действий, пока не будет нарушено условие, выполнение которого проверяется в начале цикла (рис. 1.2, в).

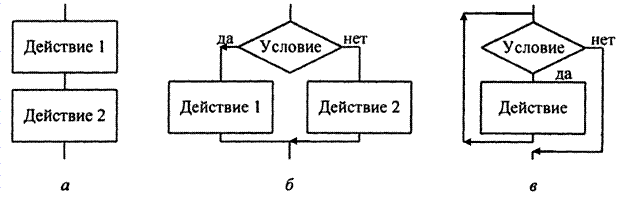
Рис. 1.2. Базовые алгоритмические структуры: следование (а), ветвление (б) и цикл-пока (в)

Таблица 1.1

Помимо базовых структур используют три дополнительные структуры, производные от базовых:

• выбор - выбор одного варианта из нескольких в зависимости от значения некоторой величины (рис. 1.3, а);

• цикл-до - повторение некоторых действий до выполнения заданного условия, проверка которого осуществляется после выполнения действий в цикле (рис. 1.3, в);

• цикл с заданным числом повторений {счетный цикл) – повторение некоторых действий указанное число раз (рис. 1.3, д).

На рис. 1.3, б, г и е показано, как каждая из дополнительных структур может быть реализована через базовые структуры.

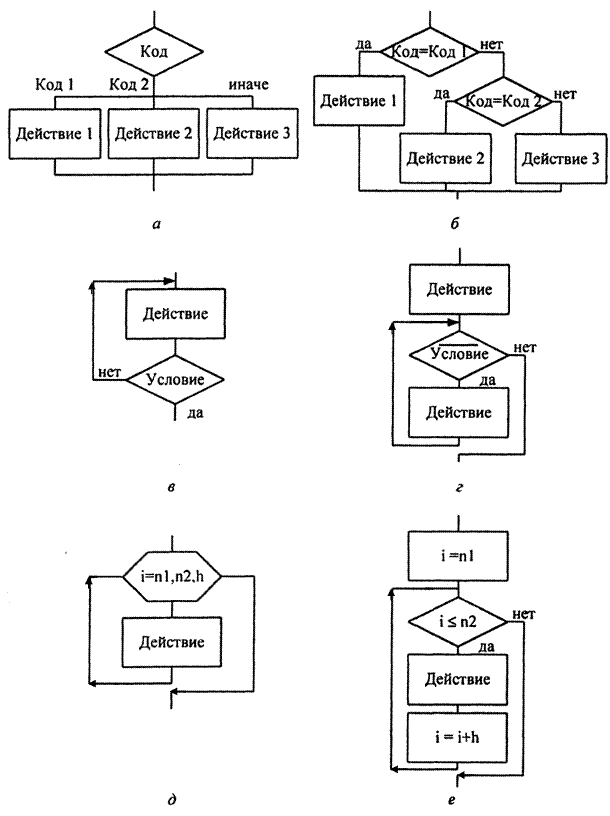
Рис.1.3. Дополнительные структуры и их реализация через базовые структуры: выбор (а-б), цикл-до (в-г) и цикл с заданным числом повторений (д-е)

Перечисленные структуры были положены в основу структурного программирования - технологии, которая представляет собой набор рекомендаций по уменьшению количества ошибок в программах [4, 8]. В том случае, если в схеме алгоритма отсутствуют другие варианты передачи управления, алгоритм называют структурным, подчеркивая, что он построен с учетом рекомендаций структурного программирования.

Схема алгоритма детально отображает особенности разработанного алгоритма.

Иногда такой высокий уровень детализации не позволяет выделить суть алгоритма. В этих случаях для описания алгоритма используют псевдокод.

Псевдокод - описание алгоритма, которое базируется на тех же основных структурах, что и структурные схемы алгоритма. Описать на псевдокоде неструктурный алгоритм нельзя.

Для каждой структуры используют свою форму описания. В литературе были предложены несколько вариантов форм псевдокодов. Один из вариантов приведен в табл. 1.2.

Таблица 1.2

Пример 1.2.Разработать алгоритм определения наибольшего общего делителя двух натуральных чисел.

Существует несколько способов определения наибольшего общего делителя двух натуральных чисел. Самым простым из них является так называемый алгоритм Евклида. Суть этого метода заключается в последовательной замене большего из чисел на разность большего и меньшего. Вычисления заканчиваются, когда числа становятся равны.

Например:

а) А

225-125 = 100

100-25 = 75

75-25 = 50

50-25 = 25

В

25-100 = 25

= 25

б) А

13-4=9

9-4=5

5-4=1

В

4-1=3

3-1=2

=2-1=1

Программа должна начинаться с ввода чисел. Заметим, что любой ввод данных пользователем должен сопровождаться запросом на ввод, чтобы пользователь знал, чего от него ждет программа после запуска. На схеме алгоритма и при записи псевдокодов этот запрос часто не указывают.

В основе алгоритма лежит циклический процесс, количество повторений которого заранее не известно (итерационный). Условие выхода из цикла - получение одинаковых чисел. Поскольку нельзя исключить, что пользователь введет равные числа, проверку будем осуществлять на входе в цикл, т.е. имеет смысл использовать цикл-пока. Если числа не равны, то при каждом проходе цикла одно из чисел (большее) должно заменяться разностью большего и меньшего. Для реализации этой замены потребуется описать оба варианта, т.е. использовать ветвление с проверкой, какое из чисел больше.

После выхода из цикла можно выводить пользователю любое из двух полученных чисел, так как они равны между собой.