Вопрос 1 геометрические искажения снимков
ВОПРОС 1 ГЕОМЕТРИЧЕСКИЕ ИСКАЖЕНИЯ СНИМКОВ
Геометрическое искажение изображения фотографируемых участков местности на снимках вызывается в основном значительными неровностями рельефа и отклонением оптической оси камеры от отвесной линии, то есть наклоном снимка относительно горизонтальной плоскости. В зависимости от этого различают на снимках искажения за рельеф и искажения за наклон снимка (рисунок 0).
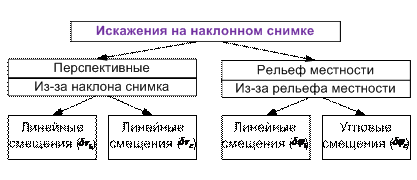
Рисунок 0 – Искажения на наклонном снимке
Искажения из-за влияния рельефа и наклона снимка могут существенно изменять форму и размеры объектов на изображении участков местности. Максимальные искажения при этом будут у краев аэрофотоснимков.
ЛИНЕЙНЫЕ СМЕЩЕНИЯ ТОЧЕК НА СНИМКЕ
ИЗ-ЗА ВЛИЯНИЯ РЕЛЬЕФА МЕСТНОСТИ
Искажения за рельеф присущи центральной проекции. Они имеются как на плановых, так и на перспективных снимках. Влияние рельефа на фотографическое изображение показано на рисунке 1.

Рисунок 1 – Искажения за рельеф местности
Точка А местности изобразится на снимке в точке а. Горизонтальной же проекцией точки В является точка В', которая при отсутствии возвышенности изобразилась бы на снимке в точке B'. Отрезок 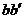 представляет собой искажение за рельеф
представляет собой искажение за рельеф 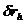 . Искажение будет тем значительнее, чем больше относительное превышение точки и дальше изображение этой точки от центра аэрофотоснимка. Поэтому на аэрофотоснимках горного района очертания местных предметов получаются искаженными. По таким снимкам расстояния и площади можно измерить только приближенно, так как значение смещения на аэрофотоснимках, расположенных на возвышенностях точек, достигает соответственно при Н=2 км 12 мм, при Н=4 км 6 мм, при H=8 км 3 мм. Такие искажения за рельеф возникают в точках, расположенных в 10 см от центра аэрофотоснимка. Если точки расположены ближе или дальше этого расстояния от центра снимка, то значения смещений пропорционально уменьшаются или увеличиваются.
. Искажение будет тем значительнее, чем больше относительное превышение точки и дальше изображение этой точки от центра аэрофотоснимка. Поэтому на аэрофотоснимках горного района очертания местных предметов получаются искаженными. По таким снимкам расстояния и площади можно измерить только приближенно, так как значение смещения на аэрофотоснимках, расположенных на возвышенностях точек, достигает соответственно при Н=2 км 12 мм, при Н=4 км 6 мм, при H=8 км 3 мм. Такие искажения за рельеф возникают в точках, расположенных в 10 см от центра аэрофотоснимка. Если точки расположены ближе или дальше этого расстояния от центра снимка, то значения смещений пропорционально уменьшаются или увеличиваются.
Рассмотрим 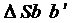 и
и 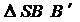 . Эти треугольники являются подобными:
. Эти треугольники являются подобными:
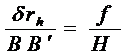 , (1)
, (1)
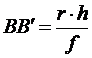 , (2)
, (2)
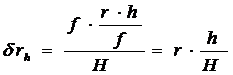 , (3)
, (3)
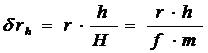 . (4)
. (4)
Анализ формулы:
1. 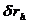 увеличивается с увеличением
увеличивается с увеличением 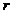 и
и 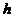 ;
;
2. 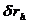 уменьшается с увеличением
уменьшается с увеличением 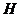 или
или 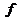 камеры;
камеры;
3. 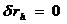 в точке надира для наклонного снимка и в точке О для горизонтального снимка;
в точке надира для наклонного снимка и в точке О для горизонтального снимка;
4. Знак 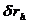 зависит от знака превышения
зависит от знака превышения 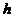 (при
(при 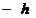
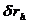 – отрицательное, соответственно при
– отрицательное, соответственно при 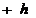
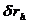 – положительное).
– положительное).
Угловые смещения точек на снимке из-за влияния рельефа местности.
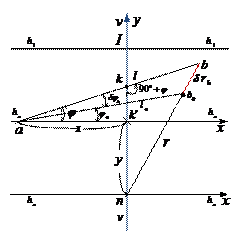
Рисунок 2 – Линейные смещения точек из-за рельефа
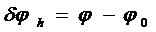 , (5)
, (5)
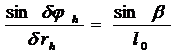 , (6)
, (6)
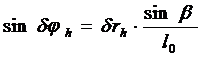 , (7)
, (7)
По теореме синусов из 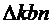 :
:
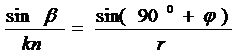 , (8)
, (8)
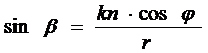 , (9)
, (9)
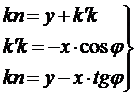 . (10)
. (10)
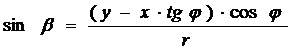 . (11)
. (11)
Подставив (11) в (7) получается выражение:
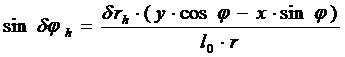 . (12)
. (12)
Анализ формулы
1) 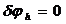 (при
(при 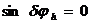 ) при
) при 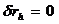 – местность плоская;
– местность плоская;
2) 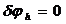 (при
(при 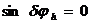 ) при
) при 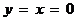 – в точке надира искажения из-за влияния рельефа отсутствуют;
– в точке надира искажения из-за влияния рельефа отсутствуют;
3) 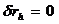 (при
(при 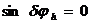 ) при
) при 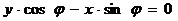 или
или 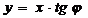 – уравнение прямой, проходящей через начало координат.
– уравнение прямой, проходящей через начало координат.
Все направления, которые проводятся через 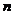 , из-за влияния рельефа не искажаются.
, из-за влияния рельефа не искажаются.
Примечание: Точку надира на снимке найти трудно, поэтому необходимы соответствующие преобразования строгой формулы (*).
4) Если вершина направлений на линии  , то координата
, то координата 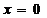 . При
. При 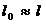
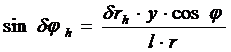 . (13)
. (13)
5) Если вершина направлений в точке 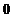 (
( 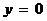 ,
, 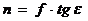 ), тогда
), тогда
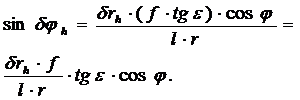 (14)
(14)
5) Для плановых снимков
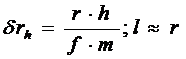 , (15)
, (15)
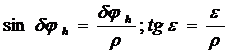 – подставим в (7)
– подставим в (7)
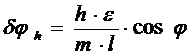 . (16)
. (16)
6) 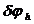 – принимает максимальное значение при
– принимает максимальное значение при 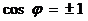 ,
, 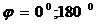
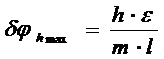 . (17)
. (17)
Линейные смещения точек на изображении из-за наклона снимка. Искажения изображения за наклон зависят от значения угла отклонения оптической оси АФА от отвесной линии (рисунок 3), фокусного расстояния фотоаппарата и расстояния от центра снимка до определяемой точки.
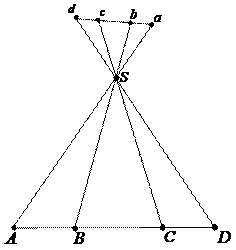
Рисунок 3 – Искажения за наклон аэрофотоснимка
Из рисунка 3, в видно, что разные расстояния между точками А, В, С, D на местности изображаются неравными отрезками на фотоснимке, и чем больше будет его наклон, тем больше будет неравенство отрезков.
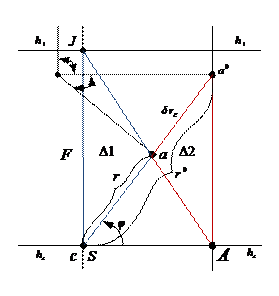
Рисунок 4 – Линейные смещения точек на наклонном снимке
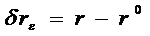 , (18)
, (18)
Так как 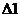 и
и 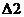 подобные, то следует записать
подобные, то следует записать
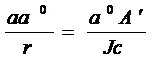 , (19)
, (19)
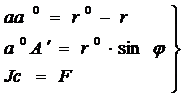 . (20)
. (20)
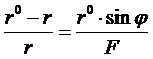 , (21)
, (21)
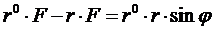 , (22)
, (22)
 , (23)
, (23)
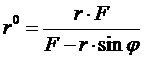 , (24)
, (24)
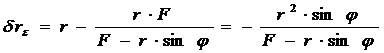 , (25)
, (25)
где 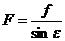 .
.
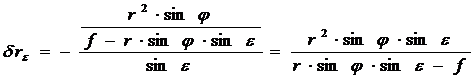 . (26)
. (26)
Эта формула для любых точек с любым наклоном.
Для планового снимка ( 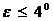 )
)
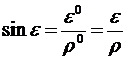 (
( 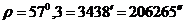 ),
),
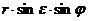 данное значение пренебрежимо мало по сравнению с
данное значение пренебрежимо мало по сравнению с 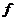 , поэтому формула (*) примет вид:
, поэтому формула (*) примет вид:
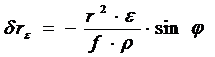 . (27)
. (27)
Анализ формулы
1) Чем больше значение фокусного расстояния 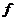 , тем значение погрешности
, тем значение погрешности 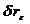 меньше;
меньше;
2) Если 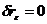
а) 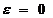 , соответственно снимок – горизонтальный;
, соответственно снимок – горизонтальный;
б) 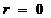 , в точке с – нулевых искажений снимок не имеет искажений;
, в точке с – нулевых искажений снимок не имеет искажений;
в) 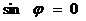 ,
, 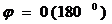 – по линии неискаженного масштаба
– по линии неискаженного масштаба 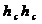 линейных смещений нет;
линейных смещений нет;
3) Максимальное значение погрешности 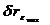 при
при 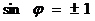 , соответственно
, соответственно 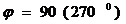
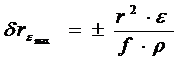 . (28)
. (28)
Анализ формулы
1. Величина 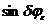 зависит от
зависит от 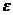 ,
, 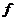 ,
, 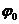 ,
, 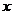 ,
, 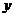 ,
, 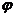 .
.
а) 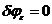 , при
, при 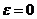 , следовательно снимок горизонтальный;
, следовательно снимок горизонтальный;
б) 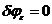 , при
, при 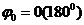 , то есть по направлению горизонтали;
, то есть по направлению горизонтали;
в) 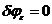 , при
, при 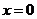 ,
, 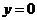 , то есть в точке нулевых искажений (с);
, то есть в точке нулевых искажений (с);
д) 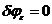 , при
, при 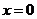 ,
, 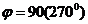 , то есть по линии
, то есть по линии  ;
;
е) 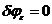 , при
, при 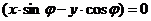 или в преобразованном виде:
или в преобразованном виде: 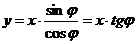 – уравнение прямой в явном виде. Проходящей через начало координат, через точку С.
– уравнение прямой в явном виде. Проходящей через начало координат, через точку С.
2.а) Для плановых снимков (когда 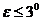 можно принять с достаточной степенью точности)
можно принять с достаточной степенью точности)
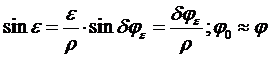 . (40)
. (40)
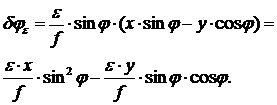 (41)
(41)
б) Если вершина направлений находится на линии 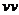 , то
, то 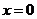 . Тогда
. Тогда
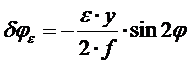 . (42)
. (42)
в) Максимальное искажение направлений ( 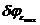 ) будут при
) будут при 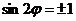 (
( 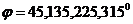 )
)
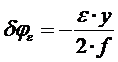 . (43)
. (43)
г) Если вершина направлений выбрана в главной точке снимка 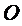 , то
, то
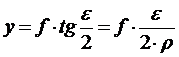 , (44)
, (44)
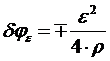 . (45)
. (45)
Для того чтобы преобразовать формулу в более удобный вид, перемножим числитель и знаменатель на одинаковые величины:
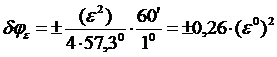 , (46)
, (46)
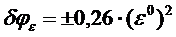 . (47)
. (47)
3. Расчет допустимого удаления центральной и главной точки.
Известно, что графическая точность определения направлений на карте составляет 4,5 минуты. Необходимо, чтобы 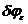 не превышала этой величины. Встает задача определить при каких углах наклона данное требование будет выполняться.
не превышала этой величины. Встает задача определить при каких углах наклона данное требование будет выполняться.
1. 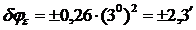 – допустимое значение;
– допустимое значение;
2. 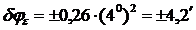 – допустимое значение;
– допустимое значение;
3. 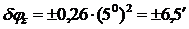 – недопустимое значение.
– недопустимое значение.
Любые направления. Проводимые через точку С не имеют 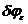 , однако точку С очень трудно найти на снимке. Поэтому в качестве вершины направлений используют точку О. На практике же обычно за вершину направлений выбирают центральную точку.
, однако точку С очень трудно найти на снимке. Поэтому в качестве вершины направлений используют точку О. На практике же обычно за вершину направлений выбирают центральную точку.
Изображения точек на снимке
Наряду с геометрической привязкой, определением масштабов снимка по направлениям, важным моментом при дешифрировании материалов КСН является определение высот объектов наблюдения (ОН). Размеры вертикальных отрезков можно определить по смещению точек отрезков (рисунок 1).
Воспользуемся уравнением связи координат точек пространства объектов и пространства изображений из фотограмметрии.
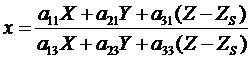 . (48)
. (48)
Логарифмируя обе части уравнения, получим 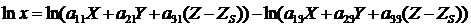 . (49)
. (49)

Рисунок 6 – Геометрическая сущность влияния кривизны Земли
Производная функции (50) по координате x и приращение Dx выразится следующим образом:
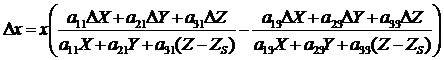 (50)
(50)
Приращения 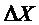 ,
, 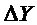 ,
, 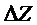 пропорциональны увеличению радиус-вектора данной точки (рисунок 6).
пропорциональны увеличению радиус-вектора данной точки (рисунок 6).
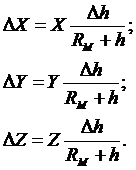 (51)
(51)
Подставив (51) в (50), получим после преобразований:
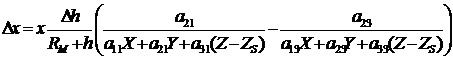 . (52)
. (52)
Выразив знаменатели в скобках через x, y, после соответствующих преобразований получим
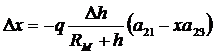 . (53)
. (53)
Выполнив аналогичные преобразования для Dy, выражение для Dy запишется в виде
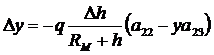 . (54)
. (54)
Результирующее смещение на снимке может быть выражено по формуле
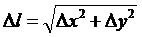 , (55)
, (55)
а направление смещения 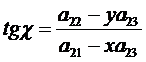 . (56)
. (56)
В предположении небольшого влияния значений координат x, y на результат, т.е. при x=0, y=0, раскрыв коэффициенты a22, a21 получим:
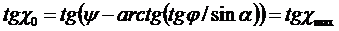 .
.
Анализ зависимостей показывает, что отображение вертикальных отрезков на снимке совпадает с направлением большой полуоси эллипса масштабных искажений. Таким образом, по направлению смещения (отображения вертикальных отрезков) на реальном снимке можно экспериментально установить положение эллипса масштабных искажений.
Результирующее смещение на снимке для центра проекции
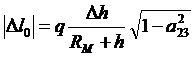 . (57)
. (57)
Из анализа выражения следует, что смещение в центре фрагмента изображения не зависит от угла рысканья.
Тогда выражение для вычисления масштаба изображения вертикальных отрезков выглядит следующим образом:
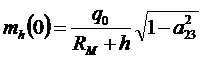 , (58)
, (58)
подставив в формулу (2.47) q0, получим:
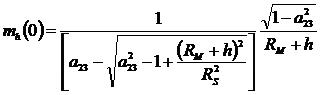 . (59)
. (59)
Формулы для масштабных искажений отображения вертикальных отрезков получены для кадровой съёмки. Тем не менее, если учесть, что в каждый момент времени строка получена при известных углах внешнего ориентирования ОС, то есть при известном законе сканирования возможно в каждый момент времени рассчитать масштаб на фрагменте изображения (положение эллипса масштабных искажений).
Изображения точек на снимке
При рассмотрении элемента изображения как центральной проекции предполагалось, что световые лучи (проектирующие лучи) распространяются по прямой линии. Однако атмосфера представляет собой среду, показатель преломления которой изменяется с изменением высоты. Это приводит к изменению траектории светового луча и смещению точки на снимке относительно ее положения при прямолинейном распространении светового луча (рисунок 7).

Рисунок 7 – Влияние рефракции на смещение изображения
точек на снимке
Рефракция – искривление траектории оптического луча при прохождении через среду переменной плотности.
В работе [23] этот вопрос рассмотрен на качественном уровне.
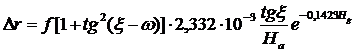 , (60)
, (60)
где 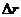 – смещение точки на изображении из-за влияния рефракции;
– смещение точки на изображении из-за влияния рефракции; 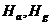 – абсолютные высоты съемки и ОН над уровнем Балтийского моря, км;
– абсолютные высоты съемки и ОН над уровнем Балтийского моря, км; 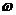 – угол наклона снимка;
– угол наклона снимка; 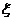 – угол смещения луча визирования от надира;
– угол смещения луча визирования от надира; 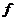 – фокусное расстояние камеры.
– фокусное расстояние камеры.
Из анализа соотношения (50) видно, что смещение изображения точки на снимке из-за влияния рефракции отсутствует только для точки надира 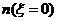 . то есть в этом случае траектория луча не исправляется. Во всех других случаях с увеличением угла
. то есть в этом случае траектория луча не исправляется. Во всех других случаях с увеличением угла 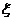 смещение точки из-за влияния рефракции увеличивается.
смещение точки из-за влияния рефракции увеличивается.
Искажения координат точки снимка, вызванные рефракцией определяются из выражений:
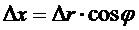 ;
;
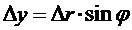 . (61)
. (61)
где 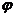 – угол, составленный радиусом-вектором с осью
– угол, составленный радиусом-вектором с осью 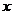 .
.
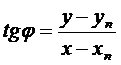 , где
, где 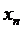 и
и 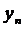 – координаты точки надира
– координаты точки надира 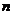 .
.
При этом необходимо сделать допущение, что плотность воздуха в пределах каждого слоя считалась одинаковой. В этом случае луч визирования находится в вертикальной плоскости, проходящей через точку местности и точку снимка, смещающуюся по направлению из точки надира.
Изображения точек на снимке
Дисторсия объектива. Дисторсия объектива определяет точность положения точек в плоскости снимка. Существуют два вида дисторсии объектива: радиальная и тангенциальная дисторсии. Дисторсия объектива объясняется тем, что световые лучи, проходя сквозь объектив там, где он искривлен, меняют свое направление и пересекаются с плоскостью снимка, отклоняясь от нормального положения. Рисунок 1.25 иллюстрирует разницу между радиальной и тангенциальной дисторсией объектива.
Рисунок 8 – Радиальная и тангенциальная
дисторсия объектива
Радиальная дисторсия объектива является причиной искажения вдоль радиальных линий, исходящих из главной точки о. Влияние радиальной дисторсии представлено как 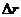 . Радиальная дисторсия объектива также обычно называется симметричной дисторсией объектива. Тангенциальная дисторсия объектива происходит под прямым углом к радиальным линиям, исходящим из главной точки о. Влияние тангенциальной дисторсии представлено как
. Радиальная дисторсия объектива также обычно называется симметричной дисторсией объектива. Тангенциальная дисторсия объектива происходит под прямым углом к радиальным линиям, исходящим из главной точки о. Влияние тангенциальной дисторсии представлено как 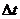 . Так как тангенциальная дисторсия очень мала по сравнению с величиной радиальной дисторсии, ею пренебрегают.
. Так как тангенциальная дисторсия очень мала по сравнению с величиной радиальной дисторсии, ею пренебрегают.
Влияние дисторсии объектива обычно определяют при проверке камеры в лабораторных условиях.
Влияние радиальной дисторсии объектива по всему изображению может быть аппроксимировано с использованием полинома. Для определения коэффициентов дисторсии объектива используется следующий полином:
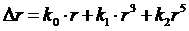 . (62)
. (62)
где 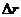 представляет радиальную дисторсию вдоль радиуса г из главной точки (Yang 1983). В большинстве паспортов камер величина дисторсии объектива представлена или как функция расстояния или как функция угла из главной точки. IМАGINЕ OrthoВАSЕ использует вычисление параметров радиальной дисторсии по обоим сценариям.
представляет радиальную дисторсию вдоль радиуса г из главной точки (Yang 1983). В большинстве паспортов камер величина дисторсии объектива представлена или как функция расстояния или как функция угла из главной точки. IМАGINЕ OrthoВАSЕ использует вычисление параметров радиальной дисторсии по обоим сценариям.
Три коэффициента ( 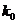 ,
, 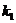 и
и 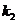 )вычисляются с использованием статистических методов. Вычисленные коэффициенты дисторсии используются для устранения влияния радиальной дисторсии для каждого измерения на снимке.
)вычисляются с использованием статистических методов. Вычисленные коэффициенты дисторсии используются для устранения влияния радиальной дисторсии для каждого измерения на снимке.
Дисторсия объектива вызывает радиальное отклонение проектирующих лучей, приводящее к радиальным смещениям точек снимка, быстро возрастающее к краям изображения. Вследствие этого изображение не подобно предмету.
Смещение точек изображения, вызванные симметричной дисторсией, направлены от центра или к центру изображения и в частном случае определяются формулой:
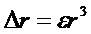 , (63)
, (63)
где 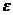 - коэффициент;
- коэффициент; 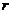 – расстояние от центра изображения до точки.
– расстояние от центра изображения до точки.
Если смещение 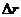 направлено от центра, то дисторсия положительная, подушкообразная (
направлено от центра, то дисторсия положительная, подушкообразная ( 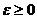 ), если смещение
), если смещение 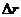 направлено к центру, то дисторсия отрицательная, бочкообразная (
направлено к центру, то дисторсия отрицательная, бочкообразная ( 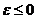 ).
).
Общее выражение для смещения точек изображения:
Для первой точки – 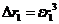 ,
, 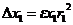 ,
, 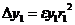 ;
;
Для второй точки:
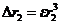 ,
, 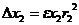 ,
, 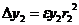 .
.
4 Ошибки, вызываемые несовершенством выравнивания фильма в плоскость (для фотографических систем)
Пленка (фильм) уклоняется от плоскости на величину 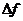 , то изображение точки А местности получим в точке
, то изображение точки А местности получим в точке 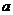 , то есть смещенным от истинного положения
, то есть смещенным от истинного положения 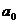 на величину:
на величину:
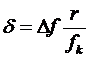 , (64)
, (64)
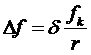 . (65)
. (65)
Деформация фильма (пленки) имеет как равномерную составляющую, изменяющую масштаб изображения, но не вносящую в него искажений, так и неравномерную или случайную составляющую, вызывающую искажение изображения.
Неравномерная деформация может иметь или случайный характер, или выражать разность деформации снимка в продольном и поперечном направлении. Последняя обычно не превышает 0,03…0,05 мм. на расстоянии в 90 мм., а случайная часть составляет около 0,02 мм.
В среднем суммарное искажение точек изображения на снимке принимают 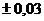 мм, хотя на краях снимка эти искажения могут быть и больше.
мм, хотя на краях снимка эти искажения могут быть и больше.
ВОПРОС 1 ГЕОМЕТРИЧЕСКИЕ ИСКАЖЕНИЯ СНИМКОВ
Геометрическое искажение изображения фотографируемых участков местности на снимках вызывается в основном значительными неровностями рельефа и отклонением оптической оси камеры от отвесной линии, то есть наклоном снимка относительно горизонтальной плоскости. В зависимости от этого различают на снимках искажения за рельеф и искажения за наклон снимка (рисунок 0).

Рисунок 0 – Искажения на наклонном снимке
Искажения из-за влияния рельефа и наклона снимка могут существенно изменять форму и размеры объектов на изображении участков местности. Максимальные искажения при этом будут у краев аэрофотоснимков.
