Визуализация результатов вычислений

Рассмотрим возможности пакета MATLAB по построению графиков функций одной переменной и поверхностей функций двух переменных. Для визуализации функций MATLAB имеет широкий набор команд, позволяющий создавать и редактировать графики для исследовательских целей и подготовки включения в издательские продукты. Графики создаются в независимом окне, имеющем графический редактор, который позволяет снабдить их необходимой текстовой и иллюстративной информацией. Иллюстрации сохраняются во всех основных графических форматах: *.gif,*.bmp,*jpg, *.tif, *.png и т.д., в том числе в формате *.eps, совместимом с Latex.

Основные команды MATLAB визуализации вычислений:

1) plot – построение графиков функций в декартовых координатах на плоскости;

2) polar – построение графиков функций в полярных координатах;

3) hist - построение гистограммы случайного вектора;

4) mesh, surf - построение поверхности графика функции двух переменных;

5) countour - построение линии уровня функции двух переменных;

6) quiver – построение векторного поля, вектор-функции или поля градиентов функции двух переменных.

Команда Plot

Требуется построить график функции y=f(x) для х 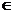[a,b]. Эту задачу решает команда plot, которая может быть использована в одном из следующих видов:

1) plot(y) % построение графика значений вектора y;

2) plot(x, y) % построение графика y(x), где x и

% y – векторы одного размера;

3) plot(x, y, s) % то же самое, параметр s задает стиль

% графического вывода;

4) plot(x1, y1, s1, x2, y2, s2, ...)

% построение нескольких графиков

% в одном окне.

Пусть параметр х принадлежит отрезку [a,b]. Зададим равномерное разбиение отрезка на n частей с шагом h. Тогда использование функции plot может быть построено следующим образом.

Пример 5.1. Пусть 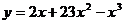, 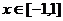. Положим n=20. Тогда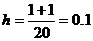

Построение графика в MATLAB будет выполнено с помощью следующих команд:

>>i=1:20; % Ввод индексов точек разбиения

>>h=0.1;

>>x=-1+i+h % Вычисление вектора х – точек

% разбиения отрезка [-1,1]

>>y=2*x+23*x.^2-x.^3 % Вычисление вектора у –

% значения в точках х

>>plot(y) % График функции y(i)

>>plot(x,y) % График функции y(x)

Результат показан на рис. 1.

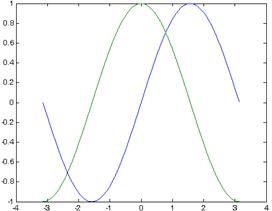
Пример 5.2. Требуется построить графики двух функций — sin(x) и cos(x) на отрезке [-p,p ] . Результат показан на рис 2.

Используем вариант команды plot(x, y), при котором значения выводимых функций содержатся в матрице y, а значения аргумента х хранятся в векторе x. При этом значения одной функции должны находиться в первом столбце, а второй функции – во втором.

>> x=-pi:pi/500:pi; % Вектор-строка аргументов

>> y1=sin(x); %Вектор-строка значений

% функции sin(x);

>> y2=cos(x); % Вектор-строка значений

% функции cos(x);

>> plot(x,[y1',y2']) % Вывод графика двух

% функций.

% Обратить внимание на

% необходимый символ “ ’ ”

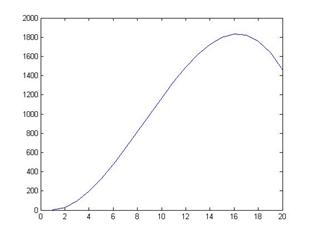Рис. 1. График Рис. 2. График

функции y(i) из функций sin(x), cos(x)

примера 5.1 из примера 5.2

5.2. Настройка параметров графического вывода команды plot

Если требуется изменить тип линий или их цвет, в списке аргументов plot добавляется параметр s: plot(x, y, s). Это строковая переменная, которая позволяет задать способ отображения линии, способ отображения точек, цвет линий и точек. Список значений переменной s, которая может быть составлена комбинацией до трех параметров, приведен в следующей таблице.

Тип линии	Тип метки	Цвет
Непрерывная - Штриховая -- Двойной пунктир : Штрих-пунктирная -.	Точка . Плюс + Звездочка * Кружок o Крестик х	Желтый y Фиолетовый m Голубой c Красный r Зеленый g Синий b Белый w Черный k

Если цвет линии не указан, он выбирается по умолчанию из шести первых цветов, с желтого до синего, повторяясь циклически.

Команда plot(x1, y1, s1, x2, y2, s2, ...) позволяет объединить в одной координатной системе (одном окне) несколько графиков функций y1(x1), y2(x2), ..., определив для каждой из них свой способ отображения.

Пример 5.3. Построить графиков трех функций на отрезке [-2π,2π] с различным стилем представления каждой из них:

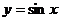- сплошной фиолетовой линией;

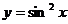- штрих-пунктирной линией с меткой + красного цвета;

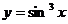- штриховкой с меткой О черного цвета;

» x=-2*pi:0.1*pi:2*pi;

» yl=sin(x);

» y2=sin(x).^2;

» y3=sin(x).^3;

» plot(x,yl,'-m',x,y2,'-.+r',x,y3,'--ok')

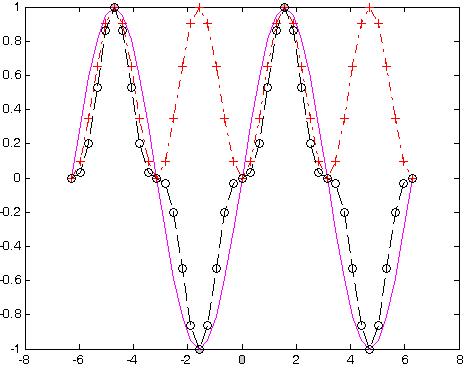
Рис. 3. Графики трех функций с разным стилем линий (Пример 5.3)

Здесь график функции yl строится сплошной фиолетовой линией, график у2 строится штрих пунктирной линией с точками в виде знака «плюс» красного цвета, а график уз строится штриховой линией с кружками черного цвета.

5.3. График функций в полярных координатах

Если функция одного аргумента задана в полярных координатах 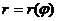, то соответствующий график строится с помощью команды polar. Команда polar( 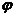, r)— строит график в полярной системе координат, представляющий собой положение конца радиус-вектора с длиной r и углом 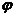. Команда polar( 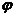, r, s)— аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы s по аналогии с командой plot.

Пример 5.4. Построить график функци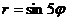и при .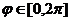

>> i = 0:1:10; t = i*2*πi/10; % Узлы аргумента

>> polar(t,sin(5*t)) % Вывод графика

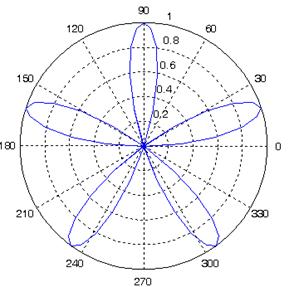
Рис.3. График функции в полярной

системе координат (пример 5.4)

5.4. Построение гистограммы

Гистограмма является одним из видов графического представления экспериментальных данных. Пусть значения величины заданы вектором Y=(Y₁…Y_n). Определяется минимальное и максимальное значения Y_i. Весь диапазон [y_min, y_max] делится на k частей. y_min=y₀ < y₁ <…< y_k =y_max. Вычисляются частоты h_j – количество значений Y_i, таких, что y_j-1<Y_i<y_j.

Команда hist(y) создает гистограмму распределения значений вектора у. Команда может быть использована в следующих вариантах:

hist(y) % гистограмма вектора h, здесь k

% равно количеству всех значений

% вектора

hist(y,n) % гистограмма вектора

% y, n – количество

% интервалов разбиения диапазона

Команда [h, x] = hist(y, n) формирует такие массивы h и x, что результатом команды bar(x, h) является гистограмма случайного вектора y.

Функция random возвращает заданного размера матрицу, состоящую из случайных чисел с заданным распределением random('name',A1,A2,A3,m,n). Параметр “name” - строка, содержащая название выбранного распределения, где величины А1, А2, А3 – параметры распределения. m и n - размер матрицы:

Пример 5.5.Получить матрицу 2х4 случайных чисел с нормальным распределением N(0,1) и вектор с распределением Пуассона.

>>rn = random('Normal',0,1,2,4)

rn =

1.1650 0.0751 -0.6965 0.0591

0.6268 0.3516 1.6961 1.7971

>>rp = random('Poisson',1:6,1,6)

rp =

0 0 1 2 5 7

Стандартное нормальное распределение генерируется командой randn. Равномерное распределение генерируется командой rand.

Пример 5.6. Построить гистограмму для 10 000 полученных с помощью функции randn случайных чисел, распределенных по нормальному закону (рис. 4).

>> x = -2.9 : 0.1 : 2.9;
>> y = randn(10000,1);
>> hist(y, x)

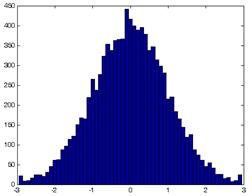
Рис.4. Гистограмма для 10 000 случайных чисел

5.5. Угловые гистограммы

Пусть задан вектор 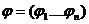, значениями которого являются величины угла направления. Требуется построить гистограмму распределения направлений. Определяется 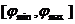- диапазон значений. Он разбивается на части, которые соответствуют секторам круга, в которые попадают векторы направлений. Команда rose вычисляет количество значений, попавших в каждый сектор и строит угловую диаграмму.

Угловые гистограммы находят применение в индикаторах радиолокационных станций, для отображения «роз» ветров и при построении других специальных графиков.

Команда rose( 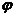) - угловая гистограмма для двадцати интервалов по данным вектора .

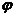Команда rose( 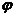, n) - угловая гистограмма для n интервалов в пределах угла от 0 до 2*рi по данным вектора tneta.

Команда rose( 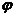, x) - угловая гистограмма по данным вектора 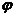со спецификацией интервалов, указанной в векторе x.

Пример 5.7.Построить случайный вектор 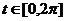, равный пятидесяти значениям равномерного распределения на отрезке [0,2p]. Построить угловую гистограмму.

>> t = 2*pi*rand(1,50);

>> rose(t)

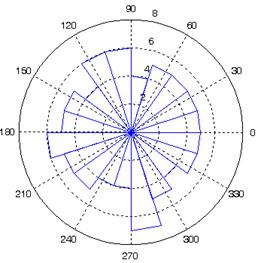
Рис.5. Угловая гистограмма примера 5.7

Замечание:

Функция h=rose(...) строит график и возвращает вектор дескрипторов графических объектов, а функция [t,r]=rose(...) сама по себе график не строит, но возвращает векторы t и r, которые нужны команде polar (t, r) для построения подобной гистограммы.