График поверхности, заданной явной функцией.

График функции 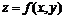можно нарисовать, используя команду plot3d(f(x,y), x=x1…x2, y=y1…y2, options). Параметры этой команды частично совпадают с параметрами команды plot. К часто используемым параметрам команды plot3d относится light=[angl1, angl2, c1, c2, c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами (angl1, angl2). Цвет определяется долями красного (c1), зеленого (c2) и синего (c3) цветов, которые находятся в интервале [0,1]. Параметр style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH – заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий, CONTOUR – линии уровня, PATCHCONTOUR – заполнитель и линии уровня. Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по умолчанию, NONE – без раскраски.

График поверхности, заданной параметрически.

Если требуется построить поверхность, заданную параметрически: x=x(u,v), y=y(u,v), z=z(u,v), то эти функции перечисляются в квадратных скобках в команде: plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2).

График поверхности, заданной неявно.

Трехмерный график поверхности, заданной неявно уравнением 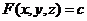, строится с помощью команды пакета plot: implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2), где указывается уравнение поверхности 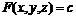и размеры рисунка по координатным осям.

График пространственных кривых.

В пакете plotимеется команда spacecurve для построения пространственной кривой, заданной параметрически: 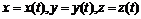. Параметры команды:

> spacecurve([x(t),y(t),z(t)],t=t1..t2),

где переменная t изменяется от t1 до t2.

Анимация.

Maple позволяет выводить на экран движущиеся изображения с помощью команд animate(двумерные) и animate3d (трехмерные) из пакета plot. Среди параметров команды animate3d есть frames – число кадров анимации (по умолчанию frames=8).

Трехмерные изображения удобнее настраивать не при помощи опций команды plot3d, а используя контекстное меню программы. Для этого следует щелкнуть правой кнопкой мыши по изображению. Тогда появится контекстное меню настройки изображения. Команды этого меню позволяют изменять цвет изображения, режимы подсветки, устанавливать нужный тип осей, тип линий и управлять движущимся изображением.

Контекстное меню настройки изображения:

Задание 2.

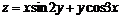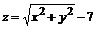1. Выполнить построение двух поверхностей и в пределах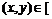 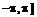. Установите переменный цвет поверхностей как функцию .

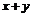> plot3d({x*sin(2*y)+y*cos(3*x), sqrt(x^2+y^2)-7}, x=-Pi..Pi, y=-Pi..Pi, grid=[30,30], axes=FRAMED, color=x+y);

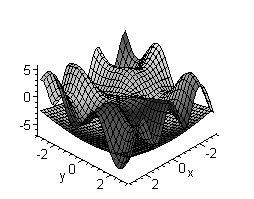
2. Построить поверхность 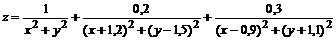вместе с линиями уровня:

> plot3d(1/(x^2+y^2)+0.2/((x+1.2)^2+(y-1.5)^2)+ 0.3/((x-0.9)^2+(y+1.1)^2), x=-2..2, y=-2..2.5, view=[-2..2, -2..2.5, 0..6], grid=[60,60], shading=NONE, light=[100,30,1,1,1], axes=NONE, orientation=[65,20], style=PATCHCONTOUR);

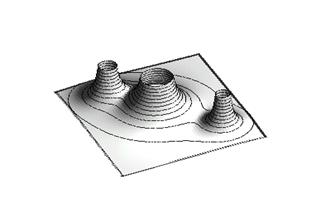
3. Построить шар :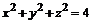

> with(plots): implicitplot3d(x^2+y^2+z^2=4,

x=-2..2, y=-2..2, z=-2..2, scaling=CONSTRAINED);

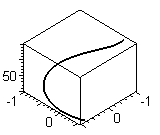
4. Построить пространственную кривую: , ,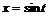

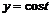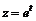
> with(plots):

> spacecurve([sin(t),cos(t),exp(t)], t=1..5, color=blue, thickness=2, axes=BOXED);

5. Нарисовать движущийся объект. Вначале наберите в командной строке:

> with(plots):

> animate3d(cos(t*x)*sin(t*y), x=-Pi..Pi,

y=-Pi..Pi, t=1..2);

Щелкните по появившемуся изображению правой кнопкой мыши. В появившемся контекстном меню выполните команду Animation®Continuous. Затем снова вызовите контекстное меню и выполните команду Animation®Play. Для того, чтобы остановить движение, выполните команду Animation®Stop. Затем поверните рисунок под другим углом и сделайте его вновь движущимся.

6. Выполните все контрольные задания. Результаты выполнения заданий покажите преподавателю. Сохраните файл со всеми выполненными заданиями на диск. Ответьте на все контрольные вопросы.

Контрольные задания.

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

- число букв в фамилии студента,

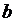- число букв в полном имени студента,

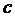- число букв в отчестве студента.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).

Задания.

1. Построить треугольник, стороны которого образуют прямые 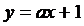, 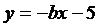и .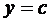

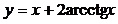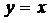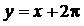2. Построить на одном рисунке графики функции и ее асимптот и . Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots (см. Задание 1.2, п.2)

3. Построить график неявной функции .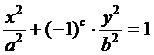

4. Построить график функции .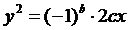

5. Построить график поверхности и определить ее вид .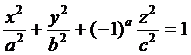

6. Построить в одной системе координат графики поверхносте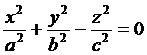й и 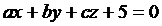и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.

7. Построить график функции 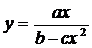на оптимальном промежутке.

Указание. Результат выполнения каждого задания необходимо оптимизировать, используя возможности Maple, сделать все необходимые подписи (заголовки, оси и т.д.).

Контрольные вопросы.

1. С помощью каких команд строятся графики на плоскости и в пространстве? Какие аргументы имеют эти команды?

2. Как называется пакет дополнительных графических команд?

3. С помощью какой команды можно построить график неявной функции? Опишите ее параметры.

4. Для чего предназначена команда display?

5. Какая команда позволяет построить двумерную область, заданную системой неравенств?

6. С помощью какой команды можно построить график пространственной кривой?

7. Какие возможности предоставляют команды animate и animate3d?