Команда plot и ее параметры.

Лабораторная работа 3.

III. Построение графиков

1. Двумерные графики.

2. Трехмерные графики. Анимация.

§1. Двумерные графики

Команда plot и ее параметры.

Для построения графиков функции f(x)одной переменной (в интервале 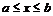по оси Ох и в интервале 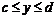по оси Оу) используется команда plot(f(x), x=a..b, y=c..d, parameters),гдеparameters– параметры управления изображением. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов.

Основные параметры команды plot:

1) title=”text”,гдеtext-заголовок рисунка (текст можно оставлять без кавычек, если он содержит только латинские буквы без пробелов).

2) coords=polar –установка полярных координат (по умолчанию установлены декартовы).

3) axes– установка типа координатных осей: axes=NORMAL – обычные оси; axes=BOXED – график в рамке со шкалой; axes=FRAME – оси с центром в левом нижнем углу рисунка; axes=NONE – без осей.

4) scaling – установка масштаба рисунка: scaling=CONSTRAINED– одинаковый масштаб по осям; scaling=UNCONSTRAINED– график масштабируется по размерам окна.

5) style=LINE(POINT) – вывод линиями (или точками).

6) numpoints=n – число вычисляемых точек графика (по умолчанию n=49).

7) сolor– установка цвета линии: английское название цвета, например,yellow– желтый и т.д.

8) xtickmarks=nxиytickmarks=ny– число меток по оси Оx и оси Оy, соответственно.

9) thickness=n,гдеn=1,2,3…- толщина линии (по умолчаниюn=1).

10) linestyle=n– тип линии: непрерывная, пунктирная и т.д. (n=1– непрерывная, установлено по умолчанию).

11) symbol=s– тип символа, которым помечают точки:BOX, CROSS, CIRCLE, POINT, DIAMOND.

12) font=[f,style,size]– установка типа шрифта для вывода текста:fзадает название шрифтов:TIMES, COURIER, HELVETICA, SYMBOL; styleзадает стиль шрифта:BOLD, ITALIC, UNDERLINE; size– размер шрифта в pt.

13) labels=[tx,ty]– надписи по осям координат:tx– по оси Оx иty– по оси Оy.

14) discont=true– указание для построения бесконечных разрывов.

С помощью команды plot можно строить помимо графиков функций y=f(x), заданной явно, также графики функций, заданных параметрически y=y(t), x=x(t), если записать команду plot([y=y(t), x=x(t), t=a..b], parameters).

Задание 1.1.

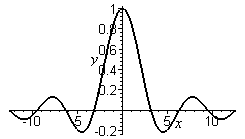
1. Построить график 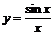жирной линией в интервале от -4p до 4p. Наберите:

> plot(sin(x)/x, x=-4*Pi..4*Pi, labels=[x,y],

labelfont=[TIMES,ITALIC,12], thickness=2);

2. Построить график разрывной функции .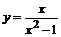

> plot(x/(x^2-1),x=-3..3,y=-3..3,color=magenta);

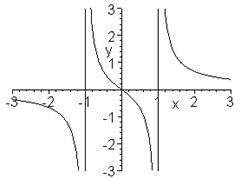
Замечание: на рисунке автоматически появляются вертикальные асимптоты.

3. Построить график параметрической кривой 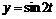, , 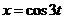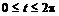в рамке. Наберите:

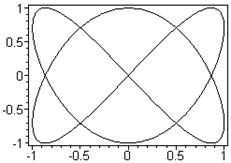
> plot([sin(2*t),cos(3*t),t=0..2*Pi], axes=BOXED, color=blue);

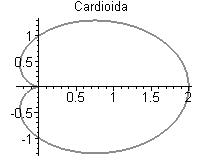
4. Построить в полярных координатах график кардиоиды 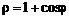с названием. Наберите:

> plot(1+cos(x), x=0..2*Pi, title="Cardioida", coords=polar, color=coral, thickness=2);

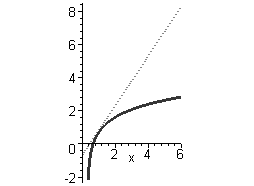
5. Построить два графика на одном рисунке: график функции 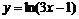и касательную к нему 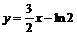. Наберите:

> plot([ln(3*x-1), 3*x/2-ln(2)], x=0..6,

scaling=CONSTRAINED, color=[violet,gold],

linestyle=[1,2], thickness=[3,2]);

Задание 1.2.

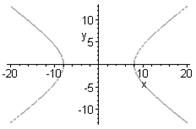
1. Построить график неявной функции (гиперболы): .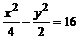

> with(plots):

> implicitplot(x^2/4-y^2/2=16, x=-20..20,

y=-16..16,

color=green, thickness=2);

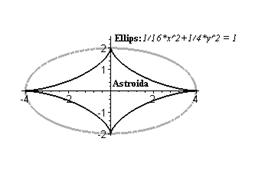
2. Построить на одном рисунке графики астроиды 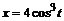, 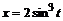( 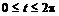) вписанной в эллипс 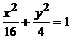. Выведите название линий Astroida и Ellips жирным шрифтом вместе с его уравнением курсивом. Для этого наберите следующие строки:

> with(plots):

> eq:=x^2/16+y^2/4=1:

> el:=implicitplot(eq, x=-4..4, y=-2..2, scaling=CONSTRAINED,

color=green, thickness=3):

> as:=plot([4*cos(t)^3,2*sin(t)^3, t=0..2*Pi],

color=blue, scaling=CONSTRAINED, thickness=2):

> eq1:=convert(eq,string):

> t1:=textplot([1.5,2.5,eq1], font=[TIMES,

ITALIC, 10], align=RIGHT):

> t2:=textplot([0.2,2.5,"Ellips:"], font=[TIMES,

BOLD,10], align=RIGHT):

> t3:=textplot([1.8,0.4,Astroida], font=[TIMES,

BOLD,10], align=LEFT):

> display([as,el,t1,t2,t3]);

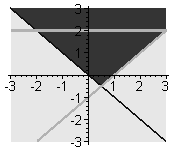
3. Построить область, ограниченную линиями: , , .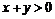

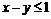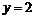> with(plots):

> inequal({x+y>0, x-y<=1, y=2}, x=-3..3, y=-3..3,

optionsfeasible=(color=red),

optionsopen=(color=blue,thickness=2),

optionsclosed=(color=green, thickness=3),

optionsexcluded=(color=yellow) );

§2. Трехмерные графики. Анимация

Анимация.

Maple позволяет выводить на экран движущиеся изображения с помощью команд animate(двумерные) и animate3d (трехмерные) из пакета plot. Среди параметров команды animate3d есть frames – число кадров анимации (по умолчанию frames=8).

Трехмерные изображения удобнее настраивать не при помощи опций команды plot3d, а используя контекстное меню программы. Для этого следует щелкнуть правой кнопкой мыши по изображению. Тогда появится контекстное меню настройки изображения. Команды этого меню позволяют изменять цвет изображения, режимы подсветки, устанавливать нужный тип осей, тип линий и управлять движущимся изображением.

Контекстное меню настройки изображения:

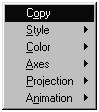
Задание 2.

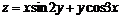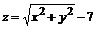1. Выполнить построение двух поверхностей и в пределах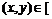 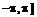. Установите переменный цвет поверхностей как функцию .

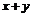> plot3d({x*sin(2*y)+y*cos(3*x), sqrt(x^2+y^2)-7}, x=-Pi..Pi, y=-Pi..Pi, grid=[30,30], axes=FRAMED, color=x+y);

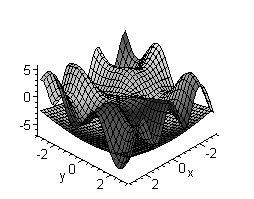
2. Построить поверхность 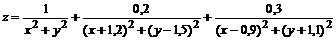вместе с линиями уровня:

> plot3d(1/(x^2+y^2)+0.2/((x+1.2)^2+(y-1.5)^2)+ 0.3/((x-0.9)^2+(y+1.1)^2), x=-2..2, y=-2..2.5, view=[-2..2, -2..2.5, 0..6], grid=[60,60], shading=NONE, light=[100,30,1,1,1], axes=NONE, orientation=[65,20], style=PATCHCONTOUR);

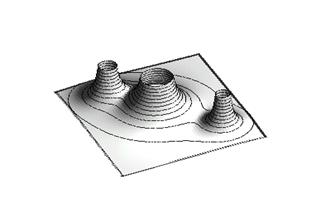
3. Построить шар :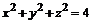

> with(plots): implicitplot3d(x^2+y^2+z^2=4,

x=-2..2, y=-2..2, z=-2..2, scaling=CONSTRAINED);

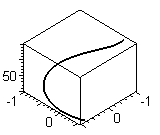
4. Построить пространственную кривую: , ,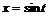

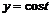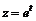
> with(plots):

> spacecurve([sin(t),cos(t),exp(t)], t=1..5, color=blue, thickness=2, axes=BOXED);

5. Нарисовать движущийся объект. Вначале наберите в командной строке:

> with(plots):

> animate3d(cos(t*x)*sin(t*y), x=-Pi..Pi,

y=-Pi..Pi, t=1..2);

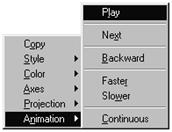Щелкните по появившемуся изображению правой кнопкой мыши. В появившемся контекстном меню выполните команду Animation®Continuous. Затем снова вызовите контекстное меню и выполните команду Animation®Play. Для того, чтобы остановить движение, выполните команду Animation®Stop. Затем поверните рисунок под другим углом и сделайте его вновь движущимся.

6. Выполните все контрольные задания. Результаты выполнения заданий покажите преподавателю. Сохраните файл со всеми выполненными заданиями на диск. Ответьте на все контрольные вопросы.

Контрольные задания.

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

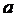- число букв в фамилии студента,

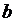- число букв в полном имени студента,

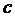- число букв в отчестве студента.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).

Задания.

1. Построить треугольник, стороны которого образуют прямые 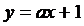, 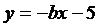и .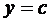

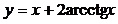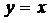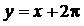2. Построить на одном рисунке графики функции и ее асимптот и . Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots (см. Задание 1.2, п.2)

3. Построить график неявной функции .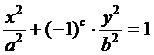

4. Построить график функции .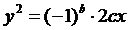

5. Построить график поверхности и определить ее вид .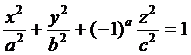

6. Построить в одной системе координат графики поверхносте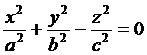й и 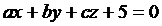и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.

7. Построить график функции 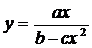на оптимальном промежутке.

Указание. Результат выполнения каждого задания необходимо оптимизировать, используя возможности Maple, сделать все необходимые подписи (заголовки, оси и т.д.).

Контрольные вопросы.

1. С помощью каких команд строятся графики на плоскости и в пространстве? Какие аргументы имеют эти команды?

2. Как называется пакет дополнительных графических команд?

3. С помощью какой команды можно построить график неявной функции? Опишите ее параметры.

4. Для чего предназначена команда display?

5. Какая команда позволяет построить двумерную область, заданную системой неравенств?

6. С помощью какой команды можно построить график пространственной кривой?

7. Какие возможности предоставляют команды animate и animate3d?

Лабораторная работа 3.

III. Построение графиков

1. Двумерные графики.

2. Трехмерные графики. Анимация.

§1. Двумерные графики

Команда plot и ее параметры.

Для построения графиков функции f(x)одной переменной (в интервале 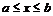по оси Ох и в интервале 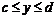по оси Оу) используется команда plot(f(x), x=a..b, y=c..d, parameters),гдеparameters– параметры управления изображением. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов.

Основные параметры команды plot:

1) title=”text”,гдеtext-заголовок рисунка (текст можно оставлять без кавычек, если он содержит только латинские буквы без пробелов).

2) coords=polar –установка полярных координат (по умолчанию установлены декартовы).

3) axes– установка типа координатных осей: axes=NORMAL – обычные оси; axes=BOXED – график в рамке со шкалой; axes=FRAME – оси с центром в левом нижнем углу рисунка; axes=NONE – без осей.

4) scaling – установка масштаба рисунка: scaling=CONSTRAINED– одинаковый масштаб по осям; scaling=UNCONSTRAINED– график масштабируется по размерам окна.

5) style=LINE(POINT) – вывод линиями (или точками).

6) numpoints=n – число вычисляемых точек графика (по умолчанию n=49).

7) сolor– установка цвета линии: английское название цвета, например,yellow– желтый и т.д.

8) xtickmarks=nxиytickmarks=ny– число меток по оси Оx и оси Оy, соответственно.

9) thickness=n,гдеn=1,2,3…- толщина линии (по умолчаниюn=1).

10) linestyle=n– тип линии: непрерывная, пунктирная и т.д. (n=1– непрерывная, установлено по умолчанию).

11) symbol=s– тип символа, которым помечают точки:BOX, CROSS, CIRCLE, POINT, DIAMOND.

12) font=[f,style,size]– установка типа шрифта для вывода текста:fзадает название шрифтов:TIMES, COURIER, HELVETICA, SYMBOL; styleзадает стиль шрифта:BOLD, ITALIC, UNDERLINE; size– размер шрифта в pt.

13) labels=[tx,ty]– надписи по осям координат:tx– по оси Оx иty– по оси Оy.

14) discont=true– указание для построения бесконечных разрывов.

С помощью команды plot можно строить помимо графиков функций y=f(x), заданной явно, также графики функций, заданных параметрически y=y(t), x=x(t), если записать команду plot([y=y(t), x=x(t), t=a..b], parameters).

Задание 1.1.

1. Построить график 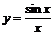жирной линией в интервале от -4p до 4p. Наберите:

> plot(sin(x)/x, x=-4*Pi..4*Pi, labels=[x,y],

labelfont=[TIMES,ITALIC,12], thickness=2);

2. Построить график разрывной функции .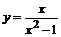

> plot(x/(x^2-1),x=-3..3,y=-3..3,color=magenta);

Замечание: на рисунке автоматически появляются вертикальные асимптоты.

3. Построить график параметрической кривой 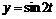, , 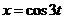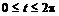в рамке. Наберите:

> plot([sin(2*t),cos(3*t),t=0..2*Pi], axes=BOXED, color=blue);

4. Построить в полярных координатах график кардиоиды 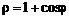с названием. Наберите:

> plot(1+cos(x), x=0..2*Pi, title="Cardioida", coords=polar, color=coral, thickness=2);

5. Построить два графика на одном рисунке: график функции 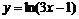и касательную к нему 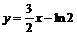. Наберите:

> plot([ln(3*x-1), 3*x/2-ln(2)], x=0..6,

scaling=CONSTRAINED, color=[violet,gold],

linestyle=[1,2], thickness=[3,2]);