Определение элементов взаимного ориентирования

Взаимное ориентирование пары снимков определяется пятью элементами. Следовательно, для их определения необходимо измерить на снимках координаты как минимум пяти соответственных точек, составить для них систему уравнений взаимного ориентирования и решить её относительно неизвестных величин.

На практике точек берут больше пяти, поэтому задачу решают методом итераций по способу наименьших квадратов (как это было сделано при определении элементов внешнего ориентирования снимка). Например, для первой системы:

1. Принимают нули в качестве приближенных значений элементов взаимного ориентирования снимков пары.

2. Выполняют измерение с целью определения координат соответственных точек x₁ , y₁ и x₂ , y_2.

3. Приближенные значения элементов взаимного ориентирования, а также элементы внутреннего ориентирования и измеренные координаты соответственных точек подставляют в уравнения (83), которое является функцией искомых величин, то есть Из-за погрешностей измерений, неточности приближенных величин, принятых в качестве неизвестных, и других причин указанная выше функция равна нулю не будет. Обозначим полученные значения через l_i, где i номер соответственной точки.

4. Принимают l_i, в качестве свободных членов, составляют уравнения поправок 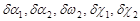, которое в общем случае выглядит следующим образом:

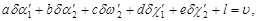(94)

где υ – остаточная величина невязки уравнения взаимного ориентирования, Коэффициенты перед поправками - частные производные функции (83) по соответствующим неизвестным. Например, коэффициенты a и b могут быть вычислены по формулам:

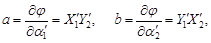
Уравнений составляют столько, сколько измерено соответственных точек.

5. При избыточном их количестве система линейных уравнений (94) решается при условии:

где Р – матрица весов измеренных координат точек снимка.

То есть составляют и решают нормальные уравнения по формулам (57) и (58), в результате чего определяют вектор поправок.

6. Вводят поправки δ к приближённым значениям элементов взаимного ориентирования, получают уточнённые значения неизвестных, которые опять принимают за приближенные значения и т. д. В качестве критерия точности определения элементов взаимного ориентирования, можно использовать величины поправок δ, поправок υ или остаточных параллаксов

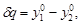(95)

вычисляемых после каждого приближения для всех точек ориентирования. Ординаты 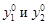определяются по второй формуле (40) через полученные элементы взаимного ориентирования и измеренные координаты x, y соответственных точек левого и правого снимков.

Для оценки точности определения элементов взаимного ориентирования в последней итерации находят весовые коэффициенты Q_jj и поправки . По этим данным вычисляют ошибку единицы веса

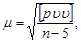(96)

а по формуле (59) - средние квадратические погрешности определения ЭВзО.

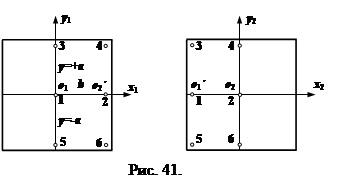При плановой аэрофотосъёмке искомые величины могут быть получены из решения приближенных уравнений (91) или (92). Используют, как правило, не 5, а шесть точек, и располагают их по стандартной схеме (рис. 41). Координаты соответственных точек 1÷6 приведены в таблице. Примем, они будут такими, если местность равнинная

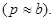
таблица
№ точки	x1	x2	y
		-b
	b
		-b	a
	b		a
		-b	-a
	b		-a

Такой выбор позволяет получить относительно простые зависимости между элементами взаимного ориентирования и поперечными параллаксами q. В первой системы ЭвзО, если подставить координаты для каждой из точек в уравнение (91)получим:

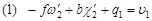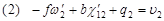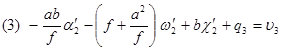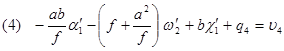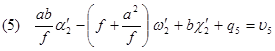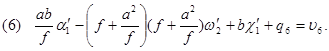(97)

Величины являются поправками к измеренным значениям поперечных параллаксов q. Они связаны с параллаксами условным уравнением, которое получается путём образования разности между суммами уравнений для точек (3), (5) и дважды (2) и для точек (4), (6) и дважды (1) т.е.

[(3)+(5)+2(2)]-[(4)+(6)+2(1)]=0.

(98)

Подставив в условное уравнение (98) уравнения взаимного ориентирования из (97), будем иметь

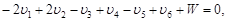(99)

где

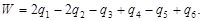(100)

Величина W - невязка, поскольку теоретически правая часть уравнения (100) должна равняться нулю. Она может служить критерием качества измерений поперечных параллаксов q на стандартных точках, так как при условии, что они равноточны, на основании зависимости (110) можно написать:

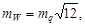
где m_q – средняя квадратическая ошибка измерения поперечных параллаксов q.

В результате допустимую невязку можно подсчитать по формуле:

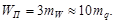(101)

Пусть поперечный параллакс q измерен с ошибкой 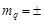0,01 мм. Тогда допуск равен 0,10 мм.

Формулы для определения ЭВзО пары снимков можно получить или путем решения системы (97) по способу наименьших квадратов или из решения ее отдельных уравнений после введения поправок 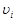в параллаксы q_i.

Во втором варианте поправки согласно (99) находятся через коррелатное уравнение из выражений:

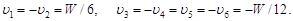(102)

После введения поправок 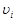система (97) становится совместной, а значения неизвестных определяются по формулам:

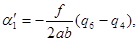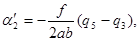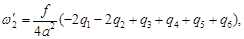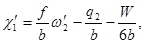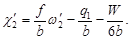(103)

Аналогично получаются формулы для второй системы ЭВзО:

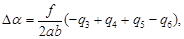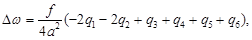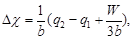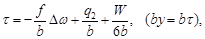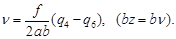(104)

Согласно (103) и (104) средние квадратические ошибки определения ЭВзО пары снимков предрасчитываются по формулам:

- для первой системы элементов:

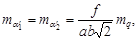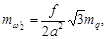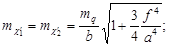(105)

- для второй:

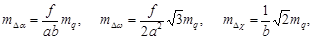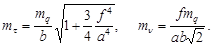(106)

Они показывают, что при одной и той же ошибке m_q измерения поперечных параллаксов точность определения ЭВзО тем выше, чем меньше величина фокусного расстояния f и больше параметры a и b стандартного расположения точек 1÷6.

В свою очередь параметр a зависит от формата снимков, а длина базиса b и от величины продольного перекрытия. При этом следует учесть, что точки 3, 4, 5 и 6 должны выбираться не ближе 2 см от края снимка, поскольку метрические качества изображения по его краям хуже, чем в центральной части.

Из сравнения формул (103) и (104) можно заключить, что между первой и второй системами ЭВзО существует следующая связь:

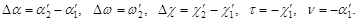(107)

Но она справедлива только с точностью до величин первого порядка малости.

Теоретические исследования [4 и проч.] показали неопределённость решения задачи определения ЭВзО, когда на местности точки 1, 3, 5 и 2, 4, 6 лежат на окружностях, а базис фотографирования расположен на образующей цилиндра, для которого эти окружности являются направляющими. Рассматриваемый случай возможен при съёмке горной местности и карьеров. При такой ситуации задача решается, но произойдет некоторое снижение точности определения координат точек местности.

4.6 Построение модели с преобразованием связок проектирующих лучей

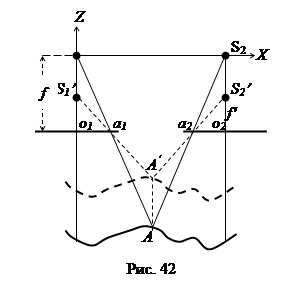Иногда строят модель, когда расстояние f^' от центра проекции до снимка не соответствует фокусному расстоянию f камеры АФА. В этом случае говорят, что связка проектирующих лучей преобразована. Для того чтобы понять к чему это приводит, изменим фокусное расстояние АФА в k раз при построении модели по паре горизонтальных снимков нормального случая съемки (Рис. 42). Из рисунка видно, что условие взаимного ориентирования пары снимков при этом не нарушится, то есть каждая пара соответственных лучей преобразованных связок будет пересекаться.

Совокупность точек, в которых пересекаются соответственные лучи преобразованных связок, называется преобразованной (афинной) моделью. Однако заметим, что при преобразовании связок проектирующих лучей точка A модели переместилась в точку A¢. Причем, отрезок AA^¢ - параллелен оси Z, так как он лежит на линии пересечения двух отвесных плоскостей S₁S₁¢a₁ и S₂S₂¢a₂. Отсюда сразу же следует, что в плане никаких изменений не происходит. Изменяется только координата Z, то есть горизонтальный масштаб 1/M_Г модели не изменится. Станет иным вертикальный масштаб 1/M_В, и он не будет теперь равен горизонтальному. Причем, из рисунка легко получить соотношение 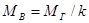между их знаменателями.

Отметим, что преобразованную модель местности можно построить не только по горизонтальным, но и по плановым снимкам.