Тема 1. Предмет фотограмметрия и дистанционное зондирование территории.

Тема 1. Предмет фотограмметрия и дистанционное зондирование территории.

План:

1. Понятие фотограмметрии и дистанционного зондирования

2. История наук

Взаимосвязь основных направлений использования снимков и наименования направлений

Дешифрирование технологически входит од­новременно в обе части названия дисциплины. Но в дистанционном зондировании роль дешифрирования превалирующая.

Взаимосвязь с др. науками:

математика, ин­форматика, физика, экология, почвоведение, инженерное обуст­ройство территории, геодезия, географические информационные системы (ГИС).

Тема 2. Физические основы аэро- и космических съемок

План лекции:

1. Электромагнитное излучение, используемое при съемках

2. Факторы, влияющие на дешифровочные свойства аэрокосмических снимков

Начальная стадия фотографического процесса, выполняемая при помощи фотоаппарата, во время которой в светочувствительном слое фотоматериала под действием света, испускаемого или отражаемого фотографируемым объектом, появляется скрытое изображение этого объекта. После фотохимической обработки оно превращается в видимое изображение.

Тема 3. Аэрофотосъемка

План лекции:

1. Технические показатели аэрофотосъемки

2. Виды аэрофотосъемки

3. Продольное и поперечное перекрытие АФС

4. Оценка качества АФС

5. Условия проведения АФС городских территорий

Виды АФС

При аэрофотографировании масштаб получаемых снимков, по экономическим соображениям, мельче масштаба создаваемого плана.

По масштабу фотографирования съемку разделяют на: крупномасштабную (1: М > 1:15 000),

среднемасштабную (1:16 000 < 1 :М< 1:50 000),

мелкомасштабную (1:М < 1:51 000),

сверхмелкомасштабную (1:М < 1:200 000).

Фотосъемку в зависимости от угла отклонения оптической оси объектива АФА от вертикали, как было рассмотрено ранее, делят на плановую и перспективную.

Плановой называют аэрофотосъемку, выполняемую при верти­кальном положении оптической оси, при этом угол отклонения допускается до 3°.

Использование гиростабилизирующих аэрофотоустановок при фотографировании местности позволяет получить снимки с углом наклона 7... 10 мин (предельное значение утла 40 мин). При созда­нии планов и карт крупного масштаба применяют снимки, полу­ченные в результате проведения плановой аэрофотосъемки.

При перспективной съемке угол отклонения оптической оси от вертикали может достигать 45°. Ее выполняют для увеличения зоны захвата снимаемой местности при обзорных или рекогнос­цировочных работах.

При планово-перспективной съемке используют несколько аэрофотоаппаратов одновременно — одним АФА проводят плано­вую съемку, другими перспективную. Это позволяет фотографи­ровать полосу местности до горизонта.

По количеству и расположению снимков различают однокадровую (одинарную), маршрутную и многомаршрутную (площад­ную) аэрофотосъемку.

Рис. .1. Схема аэрофотосъемки:

/ — двойное продольное перекрытие снимков; 2 — тройное продольное перекрытие снимков;

3 — поперечное перекрытие снимков — положение центров фотографирования;

0₁,..., 0₄ — их проекции на местности

При однокадровой фотосъемке получают одиночные снимки участков земной поверхности.

При маршрутной фотосъемке изображение полосы местности представляется в виде некоторого количества снимков, получен­ных по направлению (маршруту) полета летательного аппарата. Маршрут полета может быть прямолинейным, криволинейным или ломаным. Это зависит от вида фотографируемого объекта и целей съемки. Например, при обследовании или проектировании линейных объектов (дорог, трубопроводов, линий электропереда­чи, каналов и т. п.) съемку проводят по криволинейным или лома­ным маршрутам.

Многомаршрутная (площадная) фотосъемка представляет собой получение снимков местности с нескольких параллельных марш­рутов (рис.1). Маршруты прокладываются чаще всего по на­правлениям восток—запад—восток или север—юг—север. Пло­щадную аэрофотосъемку применяют при картографировании или обследовании больших территорий.

Тема 3. Космическая съемка

План:

1. Особенности космической фотосъемки

2. Условия получения космических снимков

3. Технические показатели космической съемки

4. Космические съемочные системы

Тема 4: Одиночный снимок

План:

1. Основные элементы центральной проекции

2. Влияние угла наклона АФА на метрические свойства снимков:

a) Смещение точек снимка

b) Изменение масштаба

c) Искажение площадей

d) Искажение направлений

3. Влияние рельефа местности на:

a) Смещение точек снимка

b) Изменение масштаба

c) Искажение площадей

d) Искажение направлений

4. Прочие факторы

Смещение точек снимка

На снимке равнинной местности (рис. 2, плоскость Е), полу­ченном при отвесном положении оптической оси съемочной ка­меры, элементы ситуации изобразятся без искажений. Сетка квадратов на местности, напр., изобразится на снимке 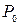подобной сеткой в масштабе: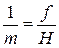

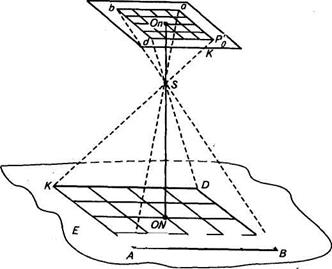Рис. 2. Горизонтальный снимок равнинной местности

Наклон камеры на некоторый угол а_Р нарушит подобие — изображение сетки квадратов перспективно преобразуется (рис. 3). На рис. 4 показаны: в позитивном варианте горизонтальный снимок Р₀ и наклонный снимок Р, а также равнинная местность Е в сечении их плоскостью главного вертикала. Снимки Р_о и Р пересекутся по горизонтали h_ch_c, так как oS= 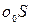=f. В прямоугольных треуголь­никах 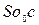и 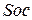общая гипотенуза и равные катеты; следователь­но, эти треугольники равны; поэтому Sc — биссектриса угла а_Р a точка с лежит на h_ch_c.

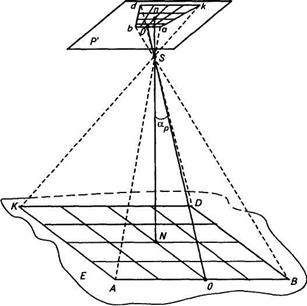
Рис. 3. Наклонный снимок равнинной местности

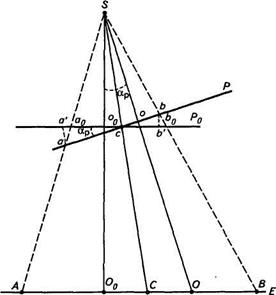
Рис. 4. Смещение точек снимка вследствие его на­клона

Произвольно выбранные на снимке точки а и b , изобразятся на снимке Р_о точками а₀ и b_о. Приняв за начало отсчетов общую для обоих снимков точку с, отложим на снимке Р_о отрезк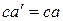и и 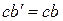. В результате получим размеры смещения изображения то­чек А и В соответственно 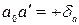и .

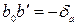Значение δ_а для точек, расположенных не на главной вертика­ли, будет зависеть также от угла φ, отсчитываемого от положитель­ного направления главной вертикали до направления, исходящего из точки с на анализируемую точку, например на точку а (рис.5), против хода часовой стрелки.

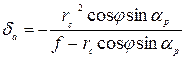(2)

где r_с — отстояние определяемой точки снимка от точки нулевых искажений.

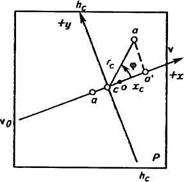
Рис.5 Правило измерения углов φ при определении смещения точек снимка вследствие его наклона

Анализ формулы показывает:

· смещения 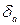,возрастают при увеличении угла 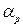и уменьшении фокусного расстояния съемочной камеры;

· точки, расположенные на горизонтали h_ch_c, не смещаются;

· максимальные смещения точек при определенном значении r_с будут в точках, располагающихся на главной вертикали (cosφ = ±l);

· точки, расположенные от горизонтали h_ch_c в сторону положи­тельных абсцисс, смещаются к точке с, а в сторону отрицательных абсцисс — от точки с (на рис.6 a_0, b_0, d₀ , e₀ — положение точек на горизонтальном снимке).

При использовании снимков плановой съемки (а < 3°) можно применять упрощенные формулы:

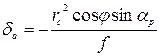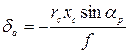или (3)

так как выражение 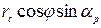имеет существенно меньшее значе­ние в сравнении с величиной f. В формуле 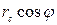выражены через х_с — абсциссу точки в системе координат v_ov — ось х, h_ch_c — ось у (рис. 5).

Изменение масштаба снимка

Различие по величине смещения точек за влияние угла наклона снимка обусловливает непостоянство масштаба по полю кадра. Ранее отмечалось, что точки, расположенные на линии h_ch_c, за влияние наклона не смещаются. Очевидно, масштаб по этой ли­нии будет постоянным и равным масштабу горизонтального снимка:

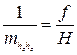(4)

Горизонталь h_ch_c называют линией неискаженных масштабов. На прочих горизонталях масштаб также будет постоянным, но на каждой горизонтали свой. Его выражают формулой:

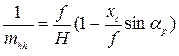(5)

в которой х_с — абсцисса горизонтали при начале координат в точке с. Масштаб вдоль главной вертикали определяют по формуле:

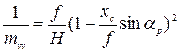(6)

Масштаб по произвольному радиальному направлению может быть вычислен по формуле:

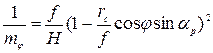(7)

В результате анализа формул 5 и 7 можно установить:

· масштаб по главной вертикали изменяется быстрее, чем после­довательно по горизонталям;

· в точке с масштаб бесконечно малого отрезка по вертикали и любому другому направлению равен масштабу в той же точке по горизонтали. Этот масштаб называют главным;

· масштаб в части снимка с положительными абсциссами мель­че, а в части с отрицательными абсциссами крупнее главного.

Используя формулы, можно решить ряд практичес­ких задач, например определить возможности выполнения метри­ческих действий непосредственно по снимку равнины с помощью его среднего масштаба. Такая задача может возникнуть, например, при нанесении промерами на снимок не изобразившихся по тем или иным причинам объектов (досъемка при дешифрировании). При создании кадастровых планов и карт досъемочные работы выполняют с использованием линейных промеров длиной 15... 25 мм на снимке. Средняя абсолютная погрешность измерения линий на снимке в полевых условиях — 0,15...0,20 мм. Средняя от­носительная погрешность при этом будет примерно 1/100. По­грешность за разномасштабность, обусловленная наклоном сним­ка, должна быть примерно той же и точнее.

Ранее установлено, что наиболее интенсивно масштаб снимка изменяется вдоль главной вертикали. Поэтому допустимость вы­полнения метрических действий непосредственно по снимку рав­нины должна определяться именно по этому направлению. Кри­терием допустимости может быть среднее относительное отклоне­ние знаменателя масштаба изображения вдоль главной вертикали (m_vv) от знаменателя главного масштаба снимка (m):

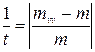
Аэрофотосъемку в целях создания кадастровых планов и карт выполняют преимущественно с использованием гиростабилизированных АФУ. Поэтому в большинстве случаев метрические дей­ствия непосредственно на снимках равнины можно выполнять с использованием единого главного масштаба, определяемого по известным значениям/и Н, с помощью измерений в натуре бази­сов или по координатам опознанных на снимках точек геодези­ческой опоры.

Для поиска путей решения той же задачи при недостаточной точности использования среднего масштаба рассмотрим рисунок 8.7, на котором тонкими линиями показана сетка квадратов (про­образ) с поворотными пунктами общей границы ао, b$, do и /₀, а также преобразованное за наклон снимка изображение прообраза. Поворотными пунктами последнего будут a, b, du I.

Для повышения наглядности характера преобразования в дан­ном случае использован простейший вариант — главная вертикаль снимка vov проходит через центр сетки и совпадает с одним из на­правлений ее сторон. Квадраты при этом преобразуются в трапеции. В общем же случае — в четырехугольники более сложной конфигурации. Для иллюстрации этого утверждения воспользуем­ся репродукцией картины Н. Н. Ге (рис. 8.8), на которой квадрат­ные элементы пола наблюдаются под значительным углом (в на­шей терминологии — под углом съемки ар) случайного направле­ния.

Вернемся к рисунку 8.7. При существенном изменении масш­таба изображения квадратов в пределах всей сетки, например в зо­нах при точках avid (обозначены окружностями), в пределах каж­дой из этих зон разномасштабность существенно меньшая.

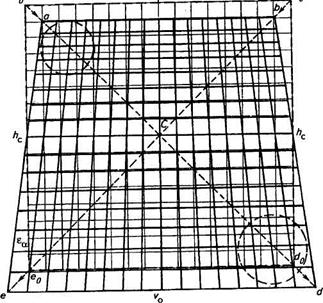Рис. 7. Искажение сетки квадратов на плановом снимке при совпадении направления главной вертикали с направлением продольных сторон исходной сетки (прообраза)

Рис. 8. Иллюстрация перспективного искажения произвольно ориентированной сетки квадратов относительно направления главной вертикали

Следовательно, необходимая точность выполнения метричес­ких действий непосредственно по снимку может быть достигнута путем использования отдельных масштабов для его разных зон — частных масштабов.

Искажение площадей

Непостоянство масштаба снимка равнины при 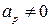приведет к искажению площадей. Относительная ошибка определения пло­щади выражается формулой, предложенной Н. Н. Веселовским:

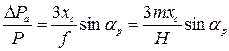
где х_с — абсцисса центра измеряемого участка в принятой ранее системе коор­динат.

Проанализируем приведенную формулу:

искажение площади уменьшается с увеличением f и соответ­ственным увеличением высоты съемки;

искажение уменьшается также с приближением участка к гори­зонтали h_ch_c . Площади участков, центр которых расположен на го­ризонтали h_ch_c, не искажаются.

Поскольку положение горизонтали обычно не известно, то это заключение имеет чисто теоретическое значение. Но в частном случае площади участков, центр которых совмещается с главной точкой (строго — с точкой с), за наклон снимка не искажаются.

Очевидно, искажения площадей участков за наклон снимка в определенных его частях будут близкими между собой и могут оказаться в пределах установленных норм. Это зна­чит, что, используя частные масштабы зон, площади участков можно определять непосредственно по снимкам.

Искажение направлений

Наличие искажения направлений на наклонном снимке можно видеть на рисунке 7. Например, направление стороны сетки ае изменилось на 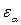. Здесь можно выявить также строгую закономер­ность в распределении значений искажений по полю снимка. В данном частном случае (v_ov направлена вдоль стороны сетки) на­правления, перпендикулярные v_ov, не исказятся. Иллюстрацией искажения направлений в общем случае может служить также репродукция картины Н. Н. Ге (рис. 8).

Определить искажения направления за наклон снимка можно с помощью рисунка 9. Исследуемое направление проходит через точки а и b (на рисунке показана правая верхняя часть снимка). Это направление пересечется с горизонталью h_ch_c в точке к под уг­лом 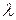. Опустив на линию аb перпендикуляр, получим точку d. Угол, образованный направления­ми перпендикуляра и главной вер­тикали, будет также равен А.. Введя в положение точки d поправку, определенную по формуле (2), найдем не смещенное за угол на­клона снимка положение этой точки — 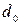. Наклонный и гори­зонтальный снимок пересекаются по линии h_ch_c. Это значит, что точка к принадлежит и неискаженному направлению, проходящему через точку 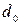. Угол 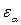, образованный при этом, будет выражать значения иска­жения направления за наклон снимка.

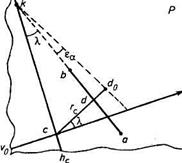Рис. 9. Геометрическая интерпрета­ция искажения направления на на­клонном снимке

Вычислить 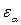можно по формуле Я. И. Гебгарта:

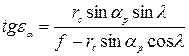
где 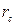— кратчайшее расстояние от точки с до исследуемого направления.

Положения точки с и главной вертикали обычно неизвестны. Поэтому полученную формулу применяют при определении воз­можности использования конкретных снимков для решения графических задач непосредственно по снимкам, вычисляя при этом предельные искажения. Для этого можно использовать упро­щенную формулу при различных аргументах и фокусных рассто­яниях

5. Влияние рельефа местности на метрические свойства снимков

Смещение точек снимка

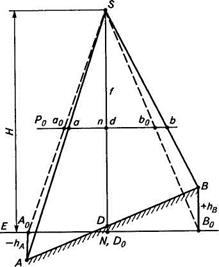Сечение горизонтального снимка Р_о и земной поверхности (с точками А, В и D) отвесной плоскостью, проходящей через центр проекции S, показано на рисунке 10. Эта плоскость пересечет снимок по линии, проходящей через точку надира п. Здесь же, в данном случае, располагаются точки о и с. Пересечем местность произвольной горизонтальной плоскостью Е. Точки А₀ и В_о — ортогональные проекции точек А и В на плоскость Е. Превыше­ния точек А и В над плоскостью Е соответственно -h_A и +h_В. На снимке точки местности и их ортогональные проекции на плос­кость Е изобразятся соответственно точками а и b, a₀ и b_о. Заме­тим, что точка а, с отрицательным превышением, сместилась от­носительно точки а₀ к точке надира, а точка b, с положительным превышением, — от точки надира. Величины a_oa и b_ob — смеще­ния точек а и b за влияние рельефа местности. Изображение точ­ки местности D, лежащей на отвесном проектирующем луче, не сместится, независимо от ее превышения над плоскостью Е. Вы­вод: точки снимка за влияние рельефа местности смещаются по направлению к точке надира или от нее в зависимости от знака превышения.

Рис. 10. Смещение точек снимка вследствие влияния рельефа местности

Смещения точек за влияние рельефа местности определяют по формуле:

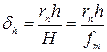
где 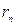— отстояние определяемой точки на снимке от точки надира; h — превыше­ние точки над горизонтальной плоскостью, принятой за исходную; H—высота съемки над той же плоскостью; т— знаменатель масштаба изображения, отнесен­ного к той же плоскости.

Тема 5: Пара снимков

План:

1. Значение зрительного аппарата человека при стереографическом восприятии

2. Стереоскопическая съемка. Стереоскопический эффект

3. Способы стереоскопического наблюдения снимков

4. Поперечный и продольный параллаксы точек снимка

5. Определение превышений точек местности по паре снимков

6. Измерительные стереоприборы

Рис. 3. Изображение отвесной линии на паре снимков идеального случая съемки

Разность ординат соответственных точек пары снимков назы­вают поперечным параллаксом точки:

На реальных снимках в общем случае q 0. Такие снимки, если значение q превышает определенные допуски, преобразуют (трансформируют). Ординаты после преобразования называют трансформированными и обозначаются и . Для трансформированных ординат должно выполняться условие:

Из этого можно сделать вывод: поперечные параллаксы явля­ются функцией некоторых величин, определяющих взаимное по­ложение пары снимков (элементов взаимного ориентирования снимков).

Разность абсцисс пары соответственных точек на левом и пра­вом снимках называют продольным параллаксом точки:

На реальных снимках абсциссы и соответственно продольные параллаксы будут искаженными (вспомним о смещении точек снимка вследствие его наклона). Следовательно, продольные па­раллаксы определяемых точек предварительно должны быть осво­бождены от искажений, т. е. трансформированы. Аналогично пре­дыдущему трансформированные абсциссы и продольные парал­лаксы обозначают добавочным символом:

Понятие фотосхемы

Фотосхемой называют фотографическое изображение местнос­ти, составленное из рабочих площадей снимков. Материалом для монтажа фотосхем служат контактные и, реже, увеличенные снимки.

Удобнее изготавливать одномаршрутные фотосхемы. Если воз­никает необходимость в обеспечении фотосхемами территорий, выходящих по площади за пределы одномаршрутной фотосхемы, монтируют несколько одномаршрутных фотосхем. Наклеивают их на основу одну под другой. Это позволяет избежать в некоторых случаях значительных расхождений ситуационных элементов в полосе поперечного перекрытия фотосхем. Маршрутные границы рабочих площадей фотосхем, проведенные по их идентичным точ­кам, могут существенно различаться по начертанию.

Возможность изготовления единой многомаршрутной фотосхе­мы при благоприятных условиях (местность равнинная, снимки гиростабилизированные) не исключается.

Преимущества фотосхем:

1) для их изготовления не требу­ется геодезической подготовки снимков и на монтажные работы требуется мало времени;

2) Фотосхемы можно использовать как приближенный картографический мате­риал на стадии предварительного изучения территорий и эскизно­го межевания.

3) фотоизображение содержит большой объем самой свежей информации о состоянии угодий, объектов инфраструктуры, водоемов и др.

4) Фотосхемы — более удобный материал, чем отдельные снимки, для тех видов дешиф­рирования, в которых требуется выявление взаимосвязей элемен­тов ландшафта, закономерностей строения рельефа на больших территориях, например при почвенном дешифрировании или ме­лиоративных изысканиях.

5) Фотосхемы — незаменимый материал при выпол­нении дешифровочных работ с борта самолета или вертолета (аэровизуальное дешифрирование).

Стереофотосхемы

При выполнении некоторых видов дешифровочных работ возникает необходимость в стереоскопи­ческом изучении рельефа на территории значительной протяжен­ности. Средне-масштабные и крупномасштабные плановые космичес­кие снимки получают с помощью длиннофокусных съемочных си­стем с узким углом поля изображения. Рельеф будет восприниматься сглаженным, за пределами порога стереоскопического восприятия останутся элементы микро- и даже мезорельефа.

Задача расширения обзорности может быть решена путем создания стерео-фотосхем.

Стереофотосхема — пара фотосхем, одна из которых смонти­рована из левых, а другая из правых половин комплекта перекры­вающихся снимков.

Принцип их изготовления заключается в следующем. Каждый снимок, кроме крайних в маршруте, используют дважды при последовательном стереоскопическом наблюдении: в одной паре как левый, в другой — как правый. Если из каждо­го снимка выделить его левую (л) и правую (п) части путем инди­видуального пореза по линиям, проходящим через пары соответ­ственных точек перекрывающихся снимков, и наклеить эти части на отдельные основы, полу­чим пару фотосхем. Наблюдая их под стереоскопом, получим стереомодель маршрута. Некоторые части снимков после пореза окажутся лишними.

Пары точек, определяющие направление порезов, должны иметь примерно одинаковые высоты. Вследствие невыполнения этого условия, образуются так называемые провалы — видимые относительные вертикальные смещения или перекосы смежных стереомоделей.

Увеличенные снимки

При недостаточной дешифрируемости снимков специалист прибегает к способам повышения дешифрируемос­ти — увеличение изображения, повышение его контраста, умень­шение смаза, фильтрация и др.

По экономическим соображениям съемку выгодно выполнять в масштабе более мелком, чем масштаб картографирования. Предел уменьшения съемочного масштаба определяется возможностями отображения на снимках необходимых объектов местности и обеспечения достаточной точности выполнения метричес­ких действий по ним. В большинстве случаев исходные снимки не обеспечивают достаточной точности, а иногда и возможности, ре­шения определенных задач.

Линейная разрешающая способ­ность зрительного аппарата человека для монокулярного и бино­кулярного зрения определяется значениями 20 и 40 мм^-1 со­ответственно. Поэтому реальная разрешающая способность зрительного аппарата уменьшится по крайней мере вдвое. В итоге оказывается, что средняя реальная разрешающая способность зрительного аппа­рата при анализе снимков характеризуется значением 7... 10 мм^-1 и меньше.

Современные аэро- и космические снимки благодаря высоко­му качеству объективов съемочных систем, использованию компенсирующих смаз изображения устройств и устойчивых в полете носителей имеют разрешающую способность 60...80 мм^-1 и более. Это дает возможность соответственно в восемь—десять раз умень­шить съемочный масштаб. Дешифрируемость таких снимков до­водят до нужного уровня путем их увеличения.

Используется два варианта:

· оптическое

· фотографическое уве­личение.

В оптическом варианте при извлечении из снимков семантической информации используют увеличивающие изображения приспо­собления — лупы, монокуляры и бинокуляры специализирован­ных приборов. Этот вариант можно применять при дешифриро­вании объектов, регистрируемых на снимках внемасштабными условными знаками (колодцы, пункты геодезической опоры и т. п.), а также при наблюдении деталей, используемых в качестве индикаторов объектов, подлежащих нанесению на карту (печных труб при раздельном показе жилых и нежилых сельских построек и т. п.).

При дешифрировании малых по площади объектов, обозначае­мых на снимках границами с условными знаками внутри контура, переход к более дорогому фотографическому увеличению неизбе­жен, если дешифрируют непосредственно снимок. Например, при создании кадастровых карт в масштабе 1:10000 пашни, многолетние насаждения и культурные пастбища на осу­шаемых землях наносят на план, если площадь их на плане пре­вышает 2 мм². На снимках, размер стороны окажется настолько малым, что размещение внутри него хотя бы одного условного знака невозможно.

Необходимость увеличения снимков обусловливается также обеспечением достаточной точности выполнения метрических ра­бот. Такие работы возникают в основном при полевой инструмен­тальной досъемке не отобразившихся на снимках объектов. Абсо­лютная погрешность фиксации концов измеряемых на снимках отрезков остается примерно постоянной при значительном (до 4...6) увеличении изображения. Дальнейшее увеличение кратности приводит к монотонному возрастанию погрешности. Поэтому относительная погрешность измерения отрезков на оптимально увеличенном снимке сокращается примерно пропорционально кратности увеличения.

Очевидно, точность измерения координат точек по увеличен­ным снимкам с помощью дигитайзера, координатографа и других измерительных устройств будет аналогично повышаться.

2. Цифровые модели местности, планы, карты

Использование новейших типов съемочных систем, переход к компьютерным технологиям и информационным системам по­зволяют получать и хранить полученную информацию о местно­сти в виде цифровых моделей, которые при необходимости могут быть представлены в визуализированном виде (на экране мони­тора или в графическом виде на бумаге). Графические планы и карты стали вторичны по отношению к цифровым моделям мест­ности.

Моделью принято называть результат описания (моделирова­ния) какого-либо объекта, процесса или явления. Модель позво­ляет заменить изучаемый объект или явление его упрощенной формой без потери необходимой информации о нем. Модель не обязана быть абсолютно тождественной самому прообразу, но должна обладать достаточностью. Под достаточностью модели по­нимают такое ее приближение к прообразу, при котором погреш­ности модели не превышают допустимые погрешности измерения параметров прообраза.

Процесс создания и изучения моделей — моделирование — одна из основных категорий теории познания: на идее моделиро­вания, по существу, базируется любой метод научного исследова­ния, как теоретический, так и экспериментальный.

Моделирование может быть семантическим (словесным), ана­логовым и математическим.

В фотограмметрии наиболее широкое распространение полу­чило математическое моделирование, которое описывает изучае­мые объекты или явления в виде:

формул (аналитические модели);

геометрических образов (геометрические модели);

массивов чисел (цифровые модели).

Цифровая модель местности (ЦММ) представляет собой много­мерную цифровую запись информации о местности на магнитном носителе. В цифровых информационных потоках информация хранится поэлементно. Каждый элемент ЦММ имеет п численных характеристик, три из которых — пространственные координаты точки местности, остальные — закодированные числами семанти­ческие характеристики этой точки.

Цифровую модель местности, содержащую информацию о пространственном положении объектов местности, а также семан­тическую информацию об этих объектах, можно представить как совокупность цифровой модели рельефа (ЦМР) и цифровой моде­ли ситуации (ЦМС).

Под ЦМР понимают массив чисел, являющихся простран­ственными координатами точек местности. ЦМС также представ­ляет собой массив чисел, каждым элементом которого являются плановые координаты поворотных точек границ объектов и зако­дированная числами семантическая информация об этих объек­тах. Содержание контуров определяется тематикой модели ситуа­ции — это могут быть топографические элементы, сельскохозяй­ственные угодья, лесотаксационные единицы, почвенные разно­сти и т. п.

Цифровые модели местности являются базой для создания ши­рокого спектра картографической продукции, используемой зем­леустроительными и кадастровыми службами. Это цифровые (электронные) карты, фотопланы, контурные фотопланы, топо­графические фотопланы, ортофотопланы, фотокарты, топографи­ческие планы, ЗБ-изображения.

Цифровая (электронная) карта (ЦК) — это объединение цифро­вой модели рельефа и нескольких цифровых моделей ситуации. Каждая ЦМС представляет собой так называемый слой ЦК. Все слои ЦК связаны между собой посредством ЦМР.

Как правило, в цифровых картах используют географические координаты, поэтому цифровые карты не имеют масштаба. При визуализации цифровая карта может быть представлена в любом

масштабе, но не крупнее того, точность которого соответствует точности исходных данных для создания ЦК.

Цифровые карты содержат значительно больший объем инфор­мации, нежели традиционные графические карты, благодаря по­слойному ее хранению.

Кроме того, цифровые карты физически не устаревают, не вет­шают. Информацию о местности на современном уровне поддер­живают ведением непрерывного мониторинга и картографическо­го дежурства.

Фотоплан — фотографическое одномасштабное изображение местности в заданном, обычно стандартном масштабе, на которое нанесена координатная сетка. Как правило, фотопланы изготав­ливают в рамках трапеций государственной или условной раз­графки или на территорию отдельных землепользовании.

На контурных фотопланах условными знаками показаны необ­ходимые элементы ситуации, некоторые элементы естественного рельефа: бровки балок, оврагов, линии резкого изменения крутиз­ны склонов, а также искусственные формы рельефа.

На топографических фототанах условными знаками показана ситуация и нанесены горизонтали.

После удаления фотоизображения контурные и топографичес­кие фотопланы превращаются соответственно в контурные и то­пографические планы.

Иногда, например при проектировании противоэрозионных мероприятий, целесообразно сохранить фотоизображение, несу­щее максимум информации об эрозионных процессах. В таких случаях на топографических фотопланах число условных знаков уменьшается до необходимого минимума. В результате получается продукция, называемая фотокартой.

Ортофотоплан — фотографическое изображение местности в ортогональной проекции. Первоначально по экономическим со­ображениям ортофотопланы изготавливали преимущественно на горные территории. В настоящее время ортофотопланы получают на различные районы местности с любыми превышениями и фор­мами рельефа.

3D-изображение — это изображение трехмерных объектов на плоскости. Эта новая форма представления пространственной ин­формации находит широкое применение в различных сферах на­учной и производственной деятельности.

Цифровые модели рельефа

Цифровая модель рельефа (ЦМР) — это цифровое представле­ние земной поверхности как непрерывного явления, описываю­щее ее с определенной точностью. Под ЦМР понимают множе­ство точек с известными геодезическими координатами и правило определения высоты любой другой точки, не вхо­дящей в это множество. Точки с известными геодезическими ко­ординатами в данном случае принято называть высотными пике­тами. Правило определения высоты называют правилом интерпо­ляции высот, или аналитической моделью рельефа (AMP).

Методы построения цифровых моделей рельефа различаются по схемам расположения высотных пикетов и по способам интер­поляции высот в промежутках между ними.

По схемам расположения высотных пикетов ЦМР делят на ре­гулярные, полурегулярные и структурные.

В регулярных моделях высотные пикеты расположены в узлах се­ток квадратов, прямоугольников или равносторонних треугольни­ков. Недостатком этих моделей является то, что наибо­лее значимые точки рельефа, находящиеся на линиях тальвегов и водоразделов, перегибах скатов, могут оказаться между узлами сетки и не отобразиться на ЦМР. В связи с этим важно выбрать оптимальный шаг сетки, так как с его увеличением возрастают по­грешности ЦМР, а с уменьшением — объем ЦМР, время и сред­ства на ее создание.

В полурегулярных моделях высотные пикеты распола­гают на поперечниках к заданным линиям. Пикеты могут нахо­диться на поперечниках либо на одинаковых расстояниях дру друга, либо на перегибах скатов. Полурегулярные ЦМР в основ­ном используют при проекти­р