Игральная кость сделана так, что вероятность выпадения определенного числа пропорциональна числу очков. Какова вероятность выпадения трех очков, если известно, что выпало нечетное число очков.

1 2 3 4 5 6

P x 2x 3x 4x 5x 6x

P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1

x+2x+3x+4x+5x+6x=1

21x=1

X=1/21

x 3x 5x

P(1)+P(3)+P(5)=1/21+3/21+5/21 = 9/21=3/7 –вероятность выпадения нечетного числа очков.

3x/9x=1/3

P=m/n=3x/9x=1/3

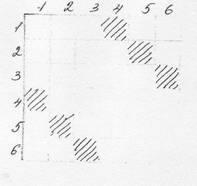
21. Брошены 2 игральные кости. Какова вероятность того, что абсолютная величина разности выпавших очков равна 3?

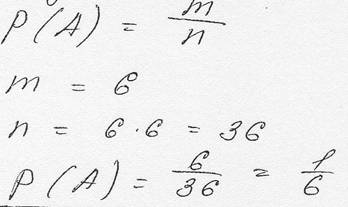
Студент в поисках книги посещает 3 библиотеки. Вероятность того, что они есть в библиотеке равны 0,4; 0,5; 0,1; а того, что они выданы или нет – равновероятные события. Какова вероятность того, что нужна книга найдена.

Решение:A-книга есть в библиотеке, B – книга не выдана.

P(B) = P(B^-) = ½

P(A1) = 0,4 P(A2) = 0,5 P(A3) = 0,1

Определим вероятность того, что нужная книга найдена:

P = P(A1)* P(B) + P(A2)*P(B) + P(A3)*P(B) = P(B)(P(A1) + P(A2) + P(A3) = 1/2 * (0,4 + 0,5 +0,1) = 1/2 * 1 = ½

Ответ: 1/2

23. Найти вероятности того, что дни рождения 12 человек прийдутся на разные месяцы года.

Решение: P(A)= m/n

m = P₁₂ = 12!

n = ^---A₁₂= 12¹²

P = 12! / 12¹² = 11! / 12¹¹ = (11*10*9*8*7*6*5*4*3*2*1) / (12*12*12*12*12⁷) = (11*5*7*5*1) / 12⁷ = 7*8*25 / 12⁷ = 1925 / 12⁷

Ответ: 1925/12⁷

24. В урне имеется 10 белых, 5 черных и 15 красных шаров. Извлекается последовательно 2 шара. Рассматриваются 2 события А - хотя бы один шар из двух вынутых красный, В - хотя бы один вынутый шар белый. Найти вероятность события С = А + В.

25.Наудачу набранный номер состоит из 5 цифр. Определить вероятность того, что все цифры в нем различны.

26.В магазин трикотажных изделий поступили носки, 60% которых получено от одной фабрики, 25% - другой и 15% - третьей. Найти вероятность того, что купленные покупателем носки изготовлены на второй или третьей фабрике.

Решение.A1-от 1 фабрики, P(A1) = 0,6;

А2 –от 2 фабрики; P(A2) = 0,25

A3 – от 3 фабрики; P(A3) = 0,15

P(A2+A3) = 0,25 + 0,15 = 0,4

Ответ: 0,4

Пассажир за получением билета может обратиться в одну из касс. Вероятность обращения в 1ую кассу составляет 0,4; во 2ую 0,35; и 3ью 0,25. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут проданы, равна для 1ой кассы 0,3; для 2ой 0,4, для 3ей 0,6. Найти вероятность того, что пассажир купит билет.

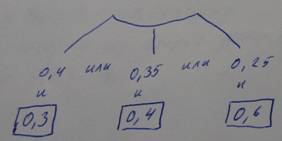P(A) –вероятность не купить билет.

P(A) =0,4*0,3 + 0,35*0,4 + 0,25*0,6 =

0,12 + 0,14 + 0,15 = 0,41

P(A1) – вероятность купить билет = 1-P(A) = 1 – 0,41 = 0,59.

Ответ: P(A1) = 0,59.

28. Бросаются 4 игральные кости. Найти вероятность того, что: а) хотя бы на одной появится 2 очка, б) на них выпадет по одинаковому числу очков.

Решение: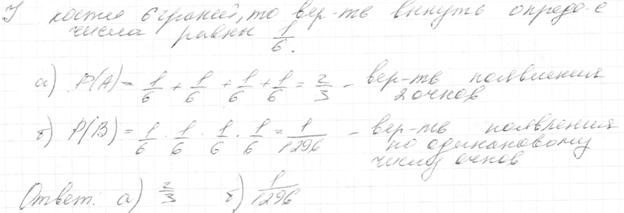

29. Из 9 жетонов, занумерованных разными однозначными цифрами, выбирается 3. Найти вероятность того, что последовательная запись их номеров покажет возрастание значений цифр.

Решение:

30. Вероятность выигрыша по лотерейному билету равна 0,1. Какова вероятность того, что выиграет хотя бы один билет из трех купленных?

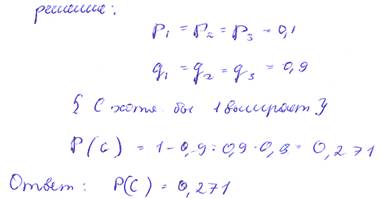
31. Из полной колоды карт(52 листа) вынимают сразу 4 карты. Найти вероятность того, что все эти карты будут разным мастей.

Решение:Вероятность вытащить конкретную масть равна C¹₁₃

C¹₁₃ = 13(количество возможных способов).

Возможность вытащить карты из 52 = C⁴₅₂ = 52! / 4!* 48! = 48!*49*50*51* 52 / 2*3*4*48! = 270725
P(A) = C¹₁₃ * C¹₁₃ * C¹₁₃ * C¹₁₃ / C⁴₅₂ = 28561 /270725 = 0,1054982

Ответ: P(A) = 0,1054982.

32. Имеется 3 урны. В первой из них 5 белых и 6 черных шаров, во второй 4 белых и 3 черных шара, в третьей 5 белых и 3 черных шара. Некто наугад выбирает одну из урн и вынимает из нее шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из второй урны.

Решение: