Аналитическое выравнивание динамических рядов способом наименьших квадратов
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание (определение тренда). В этом случае фактические урони ряда, заменяются уровнями, вычисленными на основе определенной функции, выбранной в предположении, что она наилучшим образом описывает эмпирические данные. Наиболее часто задача решается с помощью метода наименьших квадратов, когда наилучшим приближением выровненных данных к эмпирическим считается такое, при котором сумма квадратов их отклонений минимальна: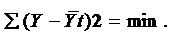 
На практике часто применяется аналитическое выравнивание по уравнению прямой:
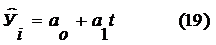
где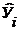 
— выровненное значение показателя; t — порядковый номер года в динамическом ряду; aо и а1 — параметры линейного уравнения.
Параметры прямой, удовлетворяющие методу наименьших квадратов, находятся из решения системы нормальных уравнений:
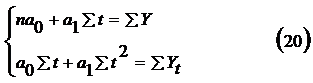
где Y – фактические уровни ряда; n — число лет ряда динамики.
Для упрощения расчетов центральному значению t придается значение 0, тогда еt = 0. С учетом этого из системы следует, что:
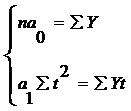Þ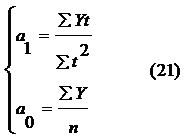 
Аналитическое выравнивание делает более четким направление тренда и одновременно дает числовую ее характеристику. Так, параметр а1 при выравнивании по прямой – это абсолютный прирост выровненного уровня за единицу времени t, или средний абсолютный прирост с учетом тенденции к равномерному росту (росту в арифметической прогрессии).
Выбор формы кривой для выравнивания осуществляется на основе анализа изучаемого явления и характера его динамики. Если рост происходит в арифметической прогрессии, то для выравнивания используют уравнение прямой. Если наблюдается динамика в геометрической прогрессии, то необходимо пользоваться уравнением кривой более высокого порядка (парабола второго порядка и т.д.).
Пример выравнивание динамического ряда объектов капитального строительства по способу наименьших квадратов представлен в таблице 2.3.
Таблица 2.3
Расчет параметров трендовой модели
| Год | Количество объектов капитального строительства, тыс. Yt | Ранг года t | Уi·t | t2 | Yt = а0 +а1t |
| (1) | (2) | (3) | (4) | (5) | (6) |
| -5 | -2700 | 547,0 | |||
| -4 | -2252 | 584,7 | |||
| -3 | -1878 | 622,4 | |||
| -2 | -1332 | 660,1 | |||
| -1 | -710 | 697,8 | |||
| 735,5 | |||||
| 773,2 | |||||
| 810,9 | |||||
| 848,6 | |||||
| 886,3 | |||||
| 924,0 | |||||
| Итого | - | Х |
По данным таблицы 2.3 и в соответствии с формулой 21 находим:
Таким образом, уравнение линейного тренда имеет вид:
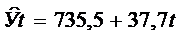
На рисунке 2.5 представлен график выравнивания динамического ряда объектов капитального строительства (ОКС), где ряд 1 – это фактическое значение уровней динамического ряда ОКС, ряд 2 – выровненное значение уровней динамического ряда ОКС.
Для ознакомления со способами наглядного представления результатов статистической обработки студент, используя исходные данные (по вариантам) проводит выравнивание динамических рядов различными методами, определяя общее направление к росту, снижению или стабилизации уровня динамического ряда. По всем показателям строятся графики.
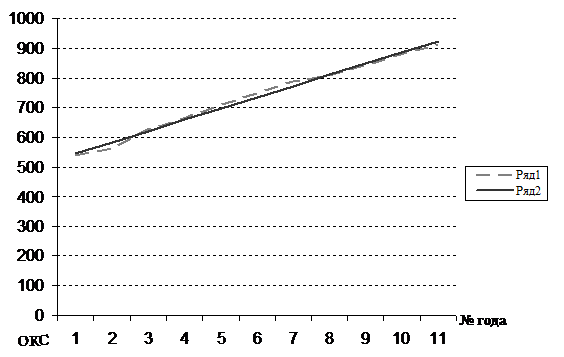
Рис.2.5. График выравнивания динамического ряда объектов капитального строительства
В результате изучения раздела 2.1 студент сможет:
- раскрыть природу выравнивания динамических рядов как базы для определения основной тенденции (тренда) развития отдельно взятого процесса или явления;
- объяснить разные методы механического и аналитического выравнивания, их содержание и направления практического использования;
- на примере выбранных динамических рядов получить практические навыки их выравнивания.