Средняя арифметическая взвешенная
На конец 2007 года размеры земельных участков, предоставленных для ведения крестьянского (фермерского) хозяйства (К(Ф)Х) в Российской Федерации, характеризуются данными таблицы 1.3.
Таблица 1.3
Земельные участки крестьянских (фермерских) хозяйств
| № п.п | Размер земельного участка, га | Удельный вес в общем числе хозяйств, % |
| до 3 | 18,0 | |
| 4 - 6 | 9,7 | |
| 7 - 11 | 13,9 | |
| 12 - 18 | 15,5 | |
| 19 - 49 | 18,7 | |
| 50 - 70 | 6,0 | |
| 71 - 101 | 5,7 | |
| 102 - 200 | 7,0 | |
| свыше 200 | 5,5 | |
| Итого | 100,0 |
Используя исходные данные (по вариантам) определяем средний размер земельного участка, предоставленный для ведения К(Ф)Х, соблюдая следующую последовательность действий:
1. Записываем исходное логическое соотношение для данной средней:
2. Обозначаем значение усредняемого признака (размер земельного участка) через X, а частоту повторения данного признака (количество К(Ф)Х) через f.
3. Так как значения усредняемого признака заданы в виде интервалов, то найдем их середины, т.е.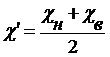 
. При этом величину первого интервала условно приравняем к величине второго, тогда его нижняя граница будет равна 1 га. Величину последнего интервала условно приравняем к величине предпоследнего, тогда его верхняя граница составит 299 га. В результате получаем следующие середины интервалов ( 
):
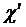2 га, 5 га, 9 га, 15 га, 34 га, 60 га, 86 га, 151 га, 249 га.
4. Роль числа К(Ф)Х в данном случае выполняет их доля в общем итоге, выраженная в процентах. Для расчета воспользуемся формулой средней арифметической взвешенной:
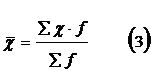
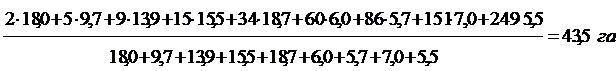
По результатам расчета - средний размер К(Ф)Х в РФ равен 43,5 га. На рисунке 1.1 представлена кольцевая диаграмма распределения земельных участков К(Ф)Х, которая позволяет наглядно отобразить результаты проведенных расчетов. Из данной диаграммы видно, что наибольший удельный вес (18%) занимают земельные участка площадью от 19 до 49 га. Участки площадью 50-70 га, 71-101 га и свыше 200 га занимают наименьший удельный вес (6%).
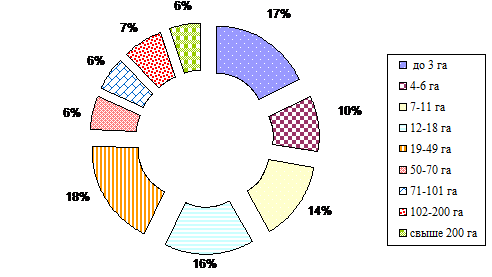
Рис. 1.1. Кольцевая диаграмма распределения земельных участков К(Ф)Х
После изучения параграфов 1.2.1-1.2.3 студент сможет:
- объяснить сущность и значение абсолютных и относительных величин, а также их применение по видам и формам выражения;
- обосновать выбор формулы средней величины;
- раскрыть содержание и особенности расчета средних величин разных видов;
- объяснить свойства и значение средней арифметической как наиболее распространенной в статистике.
Структурные средние
Помимо перечисленных в предыдущем параграфе средних величин в статистике широко применяются структурные средние, характеризующие структуру рядов распределения. Это – мода и медиана.
Мода (Mo) – это значение признака, который чаще всего встречается в статистическом ряду.
Медиана (Me) – значение признака (варианта), приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части. Медиана обладает важными свойствами. В частности, сумма модулей отклонений вариантов от медианы всегда меньше, чем сумма отклонений вариантов от любой другой величины, т.е.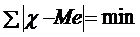 
. Это свойство медианы широко используется при определении экономической целесообразности применения отдельно взятого процесса или явления.
Медиана и мода не зависят от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами.
Студенту необходимо привести алгоритм расчета моды и медианы, используя интервальный ряд по данным о кадастровой стоимости земель населенного пункта. Пример расчета приведен в таблице 1.4.
таблица 1.4
Алгоритм расчета моды и медианы по данным кадастровой стоимости земель населенного пункта
| Кадастровая стоимость земель, тыс.руб/кв.м | Количество земельных участков (f) | Накопленная частота (S) | Середина интервала (  ) |  |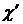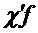
| до 14 | ||||
| 14 - 16 | ||||
| 16 - 18 | ||||
| 18 - 20 | ||||
| свыше 20 | ||||
| Итого | - | - |
По данным таблицы 1.4, наибольшая кадастровая стоимость принадлежит земельным участком в интервале 14 – 16 тыс.руб./кв.м (графа 1). Это и есть модальный интервал, ширина интервала i = 2, а нижняя граница x0 = 14, частота fмо = 30, предмодальная частота fмо-1 = 20, а послемодальная частота fмо+1 = 25.
Модальное значение кадастровой стоимости в интервальном вариационном ряду определяется по формуле:
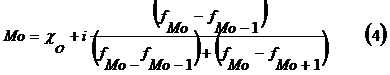
где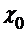 
и i – соответственно нижняя граница и величина модального интервала; 
, 
, 
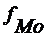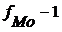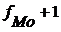- частота (частотости) модального, предмодального и послемодального интервала.
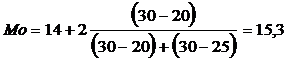тыс. руб./кв.м
Таким образом, в данной совокупности земельных участков наиболее часто встречается кадастровая стоимость в размере 15,3 тыс. руб./кв.м.
При выполнении данного задания необходимо обращать особое внимание:
1. Если используется интервальный ряд распределения то, допускается, что распределение в границах i-го интервала является равномерным, как вариант Xi, используют середину интервала (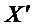 
). При этом величину открытого интервала условно считают такой же, как и величину соседнего закрытого интервала.
2. На расчет кумулятивной (накопленной) частоты, Si, характеризующей объем совокупности со значениями вариантов, не превышающих Xi. Кумулятивные частотные показатели образуются последовательным суммированием абсолютных и относительных частот: S1 = f1; S2 = f1 + f2; S3 = f1 + f2 + f3 и т.д.
Для определения медианы в ранжированном ряду необходимо вначале найти номер медианы:
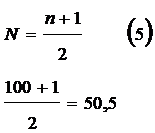
Накапливаем частоты (см. графу 2 таблица 1.4) и определяем, что 50,5 земельных участков приходятся на интервал кадастровой стоимости 16 – 18 тыс.руб./кв.м.
Нахождение медианы на данном интервале определим по формуле:
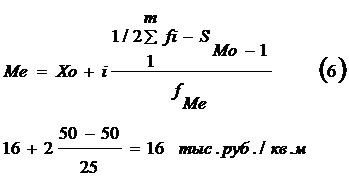
где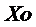 
и i – соответственно нижняя граница и величина медианного интервала; fMe – частота медианного интервала; SMe-1 – кумулятивная частота предмедианного интервала.
По расчетам определяем, половина (50%) земельных участков имеет кадастровую стоимость выше 16 тыс.руб./кв.м, и половина (50%) имеет кадастровую стоимость ниже 16 тыс.руб./кв.м.
В умеренно асимметричных рядах распределения значения моды и медианы соотносятся следующим образом:
.
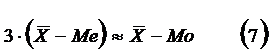В рассмотренном примере соотношение характеристик центра распределения кадастровой стоимости земельных участков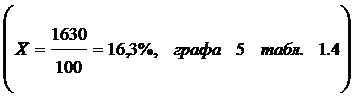 
свидетельствует об умеренной асимметрии: 3 • (16,3-16) 
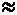16,3-15,3.
После изучения параграфа 1.2.4 студент сможет:
-раскрыть природу и практическое значение структурных средних (мода, медиана) как особой разновидности средних величин в статистике;
- проводить различие между алгебраическими средними и структурными средними величинами.