Номера складов, хлебопекарен, запрещенные и гарантированные поставки
| № Варианта | № Складов | № Хлебопекарен | Запрет перевозки | Гарантированная поставка, т/мес. |
| 1, 2, 3 | 1, 2, 3, 4 | 2x2, 3x4 | 3x3=50 | |
| 2, 3, 4, 5 | 1, 2, 5 | 2x2, 3x5 | 3x2=40 | |
| 1, 2, 4 | 1, 2, 3, 5 | 1x5, 2x3 | 4x3=45 | |
| 1, 2, 3, 4 | 3, 4, 5 | 3x3, 4x5 | 3x5=40 | |
| 1, 2, 5 | 2, 3, 4, 5 | 1x4, 5x3 | 1x5=60 | |
| 1, 2, 3, 5 | 2, 3, 5 | 5x5, 2x2 | 3x5=30 | |
| 2, 3, 4 | 2, 3, 4, 5 | 3x3, 2x5 | 4x3=45 | |
| 1, 2, 3, 5 | 1, 2, 4 | 1x2, 5x4 | 3x2=20 | |
| 2, 3, 5 | 1, 2, 3, 5 | 5x1, 3x5 | 5x2=30 | |
| 2, 3, 4, 5 | 2, 3, 4 | 5x4, 3x2 | 4x3=35 | |
| 3, 4, 5 | 1, 2, 3, 4 | 3x4, 5x1 | 4x1=40 | |
| 1, 2, 3, 4 | 1, 2, 3 | 3x2, 4x1 | 2x2=50 | |
Таблица 4.5
Запасы, потребности и тарифы перевозок
| Склады | Хлебопекарни | |||||
| Запас, т/мес. | ||||||
| Спрос, т/мес. | 77,86 | 56,78 | 58,88 | 62,44 | 73,92 |
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Какова постановка стандартной ТЗ?
2. Запишите математическую модель ТЗ.
3. Перечислите исходные и искомые параметры модели ТЗ.
4. Какова суть каждого из этапов построения модели ТЗ?
5. Раскройте понятие сбалансированности ТЗ.
6. Что такое фиктивные и запрещающие тарифы?
7. В каком соотношении должны находиться величины фиктивных и запрещающих тарифов при необходимости их одновременного использования в транспортной модели?
Лабораторная работа №5
«Теория принятия решений»
ЦЕЛЬ РАБОТЫ
Приобретение навыков построения математических моделей и решения их в Microsoft Excel.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи.
2. Постройте модель задачи.
3. Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю.
АНАЛИЗ СИТУАЦИИ В EXCEL
Рассмотрим схему принятия решений на примере конкретной ситуации.
Задача 5.1. Годовой абонемент в яхт-клубе стоит 100 ден. ед. Цена одной яхты равна 170 ден. ед. Аренда помещения и хранение яхт (от одной до 7 шт.) обходится в 530 ден. ед.
Сколько следует закупить яхт из расчета одна яхта на 5 человек, если предполагаемое число членов клуба колеблется от 10 до 25 человек?
Решение. Проанализируем для начала допустимые альтернативы решений, используя для этого информацию о возможных состояниях внешней среды. Легко заметить, что имеет смысл рассматривать количество приобретаемых яхт в диапазоне от двух до пяти (чтобы обслужить от 10 до 25 человек), т. е. 4 варианта. Перебор вариантов количества потенциальных яхтсменов ограничим также четырьмя вариантами: 10, 15, 20 и 25 человек (если полученные выводы для смежных вариантов будут существенно различаться, проведем дополнительный, уточняющий расчет). Заметим, что при реализации задачи с помощью электронной таблицы Excel проблема объема перебора снимается.
Х = (Х1,,Х2,, Х3,, Х4) = (2, 3, 4, 5) - количество яхт;
S = (S1, S2, S3, S4) = (10, 15, 20, 25) - количество членов яхт-клуба.
Занесем исходные данные в лист электронной таблицы, как это показано, например, на рисунке-5.1.
 |
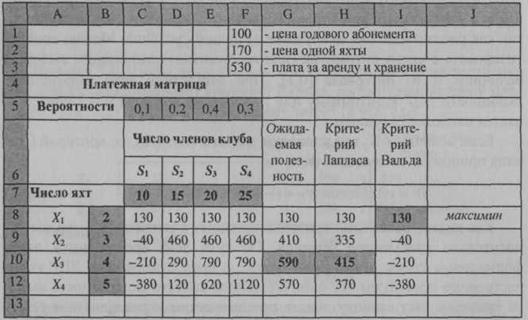Рисунок-5.1. Исходные данные и фрагмент решения задачи 5.1
Для того чтобы начать поиск решения, построим платежную матрицу, элементы которой показывают прибыль при принятии i-го решения при j-м количестве членов яхт-клуба:
Wij = 100 x min(5 x Xi; SJ) – 170 x Xi - 530,
т. е. решающее правило в данной задаче формулируется как «доход -затраты».
Использование функции МИН обеспечивает моделирование вычисления дохода в зависимости от конкретного условия SJ (спроса на яхты) и выбора решения Xi (предложение яхт). Например, если мы приобретем три яхты, а придет 25 человек, наш доход составит только 1500 ден. ед., так как 10 человек мы не сможем обслужить. Аналогично наличие яхт при отсутствии яхтсменов не принесет дохода. При реализации задачи в Excel этот факт можно также описать с помощью встроенной функции ЕСЛИ.
Для заполнения платежной матрицы в таблице Excel достаточно занести в клетку С8 следующее правило расчета:
= $F$1áMИH($B8á5;C$7) - $F$2á$B8 - $F$3
или
= ЕСЛИ ($В8á5 > C$7; $F$1á C$7; $F$1á $B8) - $F$2á$B8 - $F$3
Напомним, что знак $ позволяет не изменять соответствующую координату при копировании. Теперь осталось скопировать формулу из ячейки С8 в блок ячеек C8:F12. Для этого проще всего использовать маркер заполнения в правом нижнем углу ячейки С8.
Отрицательные значения в платежной матрице показывают, что яхт-клуб несет убытки.
Принятие решения в ситуации риска. Предположим, что имеются статистические данные, позволяющие оценить вероятность того или иного спроса на членство в яхт-клубе: Р = (0,1; 0,2; 0,4; 0,3). Найдем математическое ожидание величины прибыли для каждого из рассматриваемых вариантов решения (предложение яхт в яхт-клубе):
W1 = (130x0,1) + (130x0,2) + (130x0,4) + (130x0,3) = 130,
W2 = (-40x0,1) + (460x0,2) + (460x0,4) + (460x0,3) = 410,
W3 = (-210x0,1) + (290x0,2) + (790x0,4) + (790x0,3) = 590,
W4 = (-380x0,1) + (120x0,2) + (620x0,4) + (1120x0,3) = 570.
В координатах рассматриваемой электронной таблицы столбец G8:G12 - ожидаемая полезность - заполняем формулой: =СУММПРОИЗВ(С8:F8; $C$5:$F$5), а затем выбираем вариант решения, приносящий максимальную ожидаемую прибыль.
Вывод: в условиях рассматриваемой ситуации наиболее целесообразно закупить 4 яхты (в этом случае максимальная ожидаемая прибыль яхт-клуба составит 590 ден. ед.)
Принятие решения в ситуации неопределенности. Для применения критерия Лапласа находим:
W1= (130 + 130 + 130 + 130)/4 = 130,
W2 = (-40 + 460 + 460 + 460)/4 = 335,
W3 = 415, W4 = 370.
Для рассматриваемой электронной таблицы в ячейку с координатой Н8 заносим формулу: = CPЗHAЧ(C8:F8), копируем ее по столбцу Н до координаты HI2, а затем выбираем вариант решения, приносящий максимальную прибыль.
Вывод: в условиях равновероятности возникновения той или иной величины спроса на членство в яхт-клубе следует закупить 4 яхты и при этом можно рассчитывать на прибыль в размере 415 ден. ед.
Критерий максимина Валъда (выбор осторожной, пессимистической стратегии). Для каждой альтернативы (количество яхт в клубе) выбирается самая худшая ситуация (наименьшее значение величины прибыли) и среди них отыскивается гарантированный максимальный эффект.
Для рассматриваемой электронной таблицы находим максимальный элемент в столбце I8:I12, элементы которого являются минимальными значениями строк исходной платежной матрицы C8:F12.
Вывод: принимая решение по критерию Вальда, яхт-клубу следует закупить 2 яхты, гарантированная ожидаемая прибыль при этом равна 130 ден. ед..
Критерий Гурвица (компромиссное решение между самым худшим исходом и излишне оптимистическим). Рассмотрим изменение решения нашей задачи в зависимости от значений коэффициента оптимизма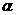 
. Соответствующий фрагмент электронной таблицы представлен на рис. 5.2. В блоке ячеек К8:М12 выделены значения, удовлетворяющие критерию Гурвица при различных 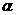, внесенных в ячейки К7:М7.
 |
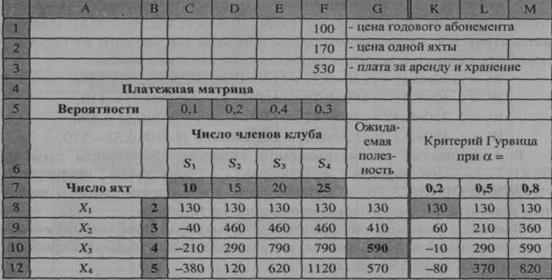Рисунок-5.2. Исходные данные и фрагмент решения задачи 5.1 по критерию Гурвица
Элементы матрицы К8:М12 рассчитываются в соответствии с (2.7) по формуле, имеющей для ячейки К8 вид
=K$7áMAKC($C8:$F8) + (1- K$7)áMИH($C8:$F8)
После копирования формулы во все ячейки блока К8:М12 выбираем вариант решения, соответствующий максимальному элементу в столбце для каждого 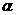. При необходимости меняем значения а в ячейках К7:М7 и получаем новые значения для выбора варианта решения.
Вывод: при 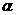≥ 0,5 следует закупить пять яхт и ожидать прибыль не меньше 370 ден. ед. (надеемся на широкую популярность нашего клуба и определенную финансовую состоятельность любителей), при 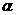= 0,2 не следует закупать более двух яхт (мы более осторожны в своих прогнозах и, скорее всего, предпочтем отказаться от создания клуба).
Критерий Сэвиджа (нахождение минимального риска). При выборе решения по этому критерию сначала матрице полезности сопоставляется матрица сожалений, представленная на рис. 5.3. Элементы матрицы, расположенной в блоке C18: F21, получены вычитанием из максимального элемента каждого столбца матрицы доходов (блок C8:F12 на рис. 5.1) всех элементов соответствующего столбца (например, первый элемент первого столбца получен как 130 - 130 = 0, второй - как 130 - (-40) = 170 и т.д.). Затем в столбце G18:G21 вычисляем максимальное значение по каждой строке матрицы C18:F21, после чего минимальный элемент в этом столбце соответствует наилучшему решению по критерию Сэвиджа.
 |
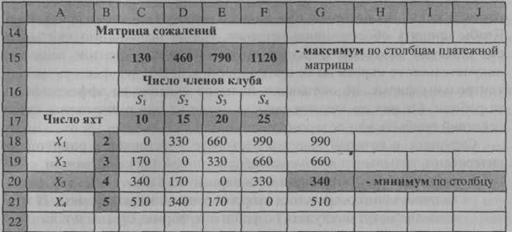Рисунок-5.3. Матрица сожалений и фрагмент решения задачи 6.1 по критерию Сэвиджа
Вывод: покупая 4 яхты для открываемого яхт-клуба, мы минимизируем риск принять неверное решение в конкретно реализовавшейся ситуации, в этом случае потери по сравнению с наилучшим вариантом решения в реализовавшейся ситуации не превысят 340 ден. ед.
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1.Можно ли использовать аддитивный критерий оптимальности (обобщённую функцию цели)для принятия решений в условиях полной определённости, если значения частных (локальных )критериев являются неоднородными?
2.Используемая в процессе принятия решений в условиях полной определённости последовательность процедур, с помощью которой все критерии приводятся к единому, безразмерному масштабу измерения называется?
3.Какой из критериев принятия решений в условиях полной неопределённости предполагает, что все состояния природы равновероятны?
4. Какой из критериев принятия решений в условиях полной неопределённости используется только для матрицы рисков?
5. Какой из критериев принятия решений в условиях полной неопределённости предполагает наступление ситуации максимального риска?
6 Какой из критериев принятия решений в условиях полной неопределённости предполагает наступление крайне благоприятной (безопасной) ситуации?
7.Критерий Лапласа для матрицы потерь (написать формулу)
8.Критерий Вальда для матрицы выигрышей(написать формулу)
9.Критерий Севиджа для матрицы рисков (написать формулу )
10. Критерий Гурвица для матрицы выигрышей(написать формулу)
5.4Варианты для самостоятельной работы
Вариант 1.Одной из фирм требуется выбрать оптимальную стратегию по техническому обеспечению процесса управления производством. С помощью статистических данных и информации соответствующих заводов - изготовителей были определены локальные критерии функционирования оборудования. Исходные данные представлены в следующей таблице:
| Варианты оборудования | Локальные критерии эффективности оборудования * | |||
| Производительность д.е. | Стоимость оборудования, д.е. | Объем памяти у. е. | Надежность у.е. | |
| I | ||||
| II | ||||
| III | 6,5 | |||
| IV | ||||
| Коэффициенты веса | 0,25 | 0,20 | 0,32 | 0,23 |
| * Значения локальных критериев в условных единицах |
Вариант 2. При выборе стратегии Rj каждому возможному состоянию природы Si соответствуют элементы Vij, являющиеся мерой потерь при принятии решения (д.е.):
| S1 | S2 | S3 | S4 | S5 | S6 | |
| R1 | -3 | |||||
| R2 | ||||||
| R3 | -2 | |||||
| R4 |
Определите оптимальную стратегию Ri используя критерии Лапласа, Вальда, Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы.
Вариант 3.При выборе стратегии Rj каждому возможному состоянию природы Sj соответствуют элементы Vij , являющиеся мерой потерь при принятии решения (д.е.):
| Стратегии | Состояние природы | |||
| S1 | S2 | S3 | S4 | |
| R1 | ||||
| R2 | ||||
| R3 |
Определите оптимальную стратегию Ri, используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы
Вариант 4.Для пяти проектов технических систем определены показатели технического совершенства конструкций :
| Проекты технических систем | Веса , т | Времени подготовки, ч. | Автомати- зации, у.е. | Мощности кВт | Унификации, у.е. |
| I | 0,088 | 1,0 | 01,0 | 0,72 | 0,614 |
| II | 1,0 | 0,8 | 0,78 | 0,81 | 0,420 |
| III | 0,358 | 0,765 | 0,782 | 0,525 | 0,915 |
| IV | 0,97 | 0,755 | 0,70 | 0,98 | 0,31 |
| V | 0,555 | 0,865 | 0,705 | 0,865 | 0,650 |
| Коэффициенты веса | 0,124 | 0,210 | 0,195 | 0,174 | 0,140 |
Выберете наилучший проект технической системы.
Вариант 5. Абсолютные показатели качества двигателей различных вариантов приведены в следующей таблице:
| Варианты двигателей | Показатели качества | ||
| мощность , л.с. | крутящий момент, кгс м | масса, кг | |
| 68,2 | |||
| 38,5 | |||
| Коэффициенты веса | 0,4 | 0,24 | 0,36 |
Найдите оптимальный вариант двигателя.
Выберете наилучший проект технической системы
Вариант 6.Определите тип электростанции, которую необходимо построить для удовлетворения энергетических потребностей комплекса крупных промышленных предприятий. Множество возможных стратегий в задаче включает следующие параметры:
R1 - сооружается гидростанция;
R2 - сооружается теплостанция;
R3 - сооружается атомная станция;
Экономическая эффективность сооружения электростанции зависит от влияния случайных факторов, образующих множество состояний природы Sj ( j = 1,5).
Результаты расчета экономической эффективности приведены в следующей таблице:
| Тип станции | Состояние природы | ||||
| S1 | S2 | S3 | S4 | S5 | |
| R1 | |||||
| R2 | |||||
| R3 |
Определите оптимальную стратегию Rj, используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы.
Вариант 7.Фирма рассматривает вопрос о строительстве станции технического обслуживания (СТО) автомобилей. Построена нижеследующая таблица ежегодных финансовых результатов (доход, д.е.):
| Проект СТО | Прогнозируемая величина дохода | |||||
| -120 | ||||||
| -160 | ||||||
| -210 | -30 | |||||
| -270 | -80 |
Определите наилучший проект СТО, используя критерии Лапласа, Вальда, Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы.
Вариант 8.При выборе стратегии Rj каждому возможному состоянию природы Si соответствуют элементы Vij, являющиеся мерой потерь при принятии решения (д.е.):
| S1 | S2 | S3 | S4 | S5 | S6 | |
| R1 | -3 | |||||
| R2 | ||||||
| R3 | -2 | |||||
| R4 |
Определите оптимальную стратегию Rj, используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы.
Вариант 9.Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля Rj (j = 1,4). Значения экономической эффективности для различных проектов и состояний приведены в следующей таблице (д.е):
| Проекты | Состояние природы | ||
| S1 | S2 | S3 | |
| R1 | |||
| R2 | |||
| R3 | |||
| R4 |
Определите оптимальную стратегию Rj, используя критерии Лапласа, Вальда,
Сэвиджа и Гурвица (а = 0,5, а = 1). Сделайте выводы.
Вариант 10.Для шести вариантов транспортных устройств определены показатели технического совершенства конструкций:
| Варианты транспортных устройств | Скорости, км/ч | Прочности, у.е. | Грузоподьем ность, т | Устойчи- вости, у.е. | Металло- емкости, у.е. | Мощности, л.с. |
| I | 10,0 | 0,798 | 0,92 | 1,0 | 1,0 | 0,77 |
| II | 9,0 | 1,0 | 0,65 | 0,92 | 0,94 | 0,92 |
| III | 12,0 | 0,93 | 0,924 | 1,0 | 0,98 | 0,95 |
| IV | 7,0 | 0,96 | 0,91 | 0,915 | 0,99 | 0,85 |
| V | 6,0 | 0,78 | 0,75 | 0,967 | 0,8 | 0,3 |
| Коэффициенты веса | 0,210 | 0,195 | 0,174 | 0,157 | 0,124 | 0,140 |
Выберете наилучший вариант технического совершенства конструкций