Возможные ошибки при вводе условий задач ЛП

Если при решении задачи ЛП выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel. Поэтому, прежде чем делать вывод о принципиальной невозможности нахождения оптимального решения задачи, ответьте на вопросы из табл.1.4.

Таблица 1.4 Список вопросов, позволяющих выявить ошибки ввода условия задачи в Excel

Месторасположение в Excel

Экранная форма

Окно "Поиск решения"

Окно "Поиск решения" Поле "Изменяя ячейки"

Экранная форма, Окно "Поиск решения" Поле "Ограничения"

Окно "Поиск решения" Поле "Ограничения"

Окно "Параметры поиска решения"

Вопрос

Правильно ли Вы ввели численные значения и знаки (+, —) коэффициентов целевой функции и ограничений, правых частей ограничений ?

Сбалансирована ли двухиндексная задача?

Правильны ли формулы в целевой ячейке и в ячейках левых частей ограничений? Для наглядности проверки поставьте курсор на ячейку с формулой и сделайте двойной щелчок левой клавишей мыши. Рамкой в экранной форме будут выделены ячейки, участвующие в данной формуле (см. рис.1.4, 1.5).

Правильно ли указан адрес целевой ячейки?

Правильно ли указано направление оптимизации ЦФ?

Правильно ли указаны адреса ячеек переменных?

Правильно ли введены знаки ограничений (<=, >=, =) ?

Правильно ли указаны адреса ячеек левых и правых частей ограничений?

Не забыли ли Вы задать требование неотрицательности переменных?

Не забыли ли Вы задать требования по единичному значению верхней границы переменных (для задач с булевыми переменными)

Не забыли ли Вы задать условие целочисленности переменных (согласно условию задачи)?

Проверьте правильность установки параметров (см. подразд.1.3.1.2)

№

ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ

1. Каковы основные этапы решения задач ЛП в MS Excel?

2. Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений?

3. В чем смысл использования символа $ в формулах MS Excel?

4. В чем различие использования в формулах MS Excel символов ; и :?

5. Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения?

6. Каким образом в MS Excel задается направление оптимизации ЦФ?

7. Какие ячейки экранной формы выполняют иллюстративную функцию, а какие необходимы для решения задачи?

8. Как наглядно отобразить в экранной форме ячейки, используемые в конкретной формуле, с целью проверки ее правильности?

9. Поясните общий порядок работы с окном "Поиск решения".

10. Каким образом можно изменять, добавлять, удалять ограничения в окне "Поиск решения"?

11. Какие сообщения выдаются в MS Excel в случаях: успешного решения задачи ЛП; несовместности системы ограничений задачи; неограниченности ЦФ?

12.Объясните смысл параметров, задаваемых в окне "Параметры поиска решения".

13. Каковы особенности решения в MS Excel целочисленных задач ЛП?

14. Каковы особенности решения в MS Excel двухиндексных задач ЛП?

15. Каковы особенности решения в MS Excel задач ЛП с булевыми переменными?

ВАРИАНТЫ

Используя MS Excel, найти решение для модели ЛП (табл.1.5) в двух вариантах:

1) нецелочисленном;

2) целочисленном.

Показать решение преподавателю и защитить лабораторную работу.

Таблица 1.5 - Варианты задач к лабораторной работе №1

№ варианта	Математическая модель

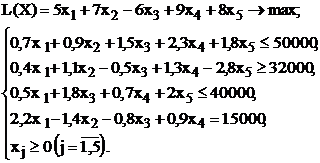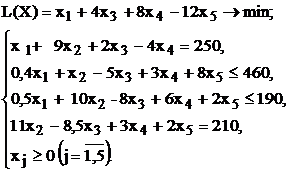№ варианта	Математическая модель

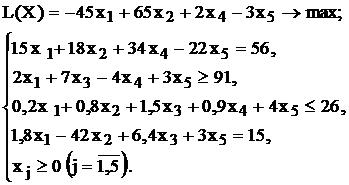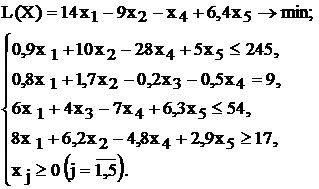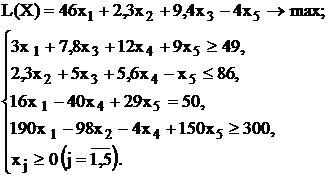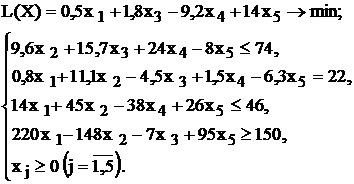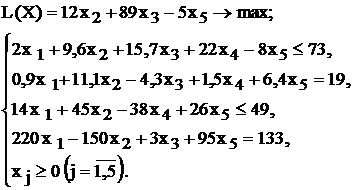№ варианта	Математическая модель

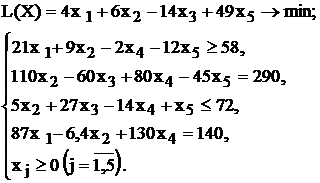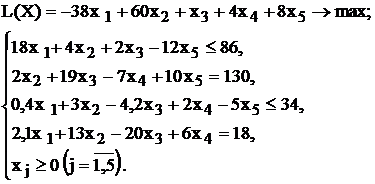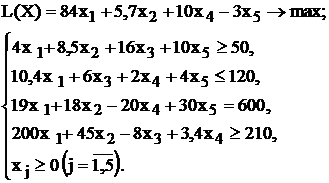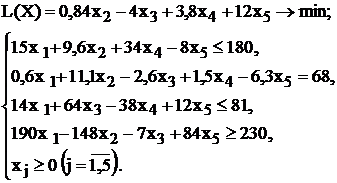Лабораторная работа №2

«РЕШЕНИЕ ЗАДАЧ СИМПЛЕКСНЫМ МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ»

ЦЕЛЬ РАБОТЫ

1. Построить экономико-математическую модель задачи.

2. Матрицу задачи ввести в компьютер.

3. Выполнить необходимые настройки и решить задачу.

4. Проанализировать полученное решение.

5. Выполнить вариантные решения по перечисленным ниже пунктам.

Условие задачи.

Для выращивания зерновых культур (пшеницы, ячменя и гороха) выделяется 800 га пашни, 12000 чел.-ч трудовых ресурсов и 1300 ц минеральных удобрений. Технико-экономические коэффициенты в расчёте на 1 га посева каждой культуры приведены в таблице.

Показатели	Пшеница	Ячмень	Горох
Затраты труда, чел.-ч
Норма внесения удобрений, ц	1,4	1,2	0,9
Урожайность, ц.

Критерий оптимальности – максимум производства зерна.

Вариантные решения

Примечание. Для каждого варианта сохранить отчёты по результатам и устойчивости, затем вернутся к первоначальному условию.

1. Ввести в план посевы культуры, которая получалась невыгодной, добавив в модель 4-е ограничение.

2. Изменить коэффициент целевой функции при этой переменной таким образом, чтобы культура стала выгодной.

3. Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.

4. Увеличить объем любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным.

5. Предусмотреть полное использование того производственного ресурса, который не является дефицитным.

6. В том случае, когда в последнем варианте не получается оптимального решения, определить, какими должны быть объёмы производственных ресурсов (дефицитных в первоначальном решении), чтобы все три ресурса использовались полностью.

Все необходимые изменения для получения нового варианта решения задачи делаются в исходной матрице. В соответствии с ними вносятся изменения в окне «Поиск решения» и задача решается повторно. По окончании решения в типовом отчёте по результатам можно будет сравнить новое решение (столбец «Результат») с предыдущим (столбец «Исходно»).

Изменение коэффициента при переменной или объёма ограничения. Для этого достаточно исправить коэффициент при переменной или объём ограничения в исходной матрице и повторно решить задачу, не внося исправлений в настройки в окне «Поиск решения».

Добавление ограничения (ограничений) в матрицу. Ограничения вводятся после последнего, имеющегося в матрице. В ячейку по столбцу «Значение по решению» копируется формула из предыдущей строки, после чего в окне «Поиск решения» добавляется условие на эти ограничения и задача решается повторно.

Удаление лишних ограничений. Из матрицы удаляются все лишние строки, после чего соответствующие условия удаляются в окне «Поиск решения» и задача решается повторно.

Ввод в оптимальный план переменной, не вошедшей в него (получившей нулевое значение) или изменение значения какой-либо переменной. Для этого в матрицу добавляется ограничение на соответствующую переменную.

Например, нужно, чтобы площадь посева ячменя в нашей задаче была равна 280 га. Ограничение на эту переменную запишется следующим образом: Х2=280. Это ограничение вводится в матрицу под номером 5.

2.1.Варианты для самостоятельной работы

Вариант 1

Определить рациональное сочетание посевов ржи, пшеницы и гречихи. Для их возделывания выделяется 800 га пашни, 12000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Рожь	Пшеница	Гречиха
Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р.	1,6	1,4	0,8

Критерий оптимальности – максимум товарной продукции в денежном выражении

Вариантные решения

Ввести в план посевы культуры, которая получилась невыгодной, добавив в модель 4-е ограничение

Вариант 2

Определить рациональное сочетание посевов пшеницы, ячменя и проса. Для их возделывания выделяется 1000 га пашни, 13000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Пшеница	Ячмень	Просо
Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р.	1,4	1,2	1,0

Критерий оптимальности – максимум товарной продукции в денежном выражении.

Вариантные решения

Изменить коэффициент целевой функции при переменной таким образом, чтобы культура стала выгодной

Вариант 3

Определить рациональное сочетание посевов ячменя, овса и гречихи. Для их возделывания выделяется 1200 га пашни. 15000 чел.-дней трудовых ресурсов и 1200 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Ячмень	Овёс	Гречиха
Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р.	1,2	1,0	0,8

Критерий оптимальности – максимум товарной продукции в денежном выражении.

Вариантные решения

Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.

Вариант 4

Определить рациональное сочетание посевов ржи, ячменя и овса. Для их возделывания выделяется 1500 га пашни, 23000 чел.-дней трудовых ресурсов и 1900 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Рожь	Ячмень	Овёс
Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р.	1,6	1,2	1,0

Критерий оптимальности – максимум товарной продукции в денежном выражении

Вариантные решения

Увеличить объём любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным

Вариант 5

Определить рациональное сочетание посевов пшеницы, ячменя и овса. Для их возделывания выделяется 2000 га пашни, 25000 чел.-дней трудовых ресурсов и 2400 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Пшеница	Ячмень	Овёс
Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р.	1,4	1,2	0,8

Критерий оптимальности – максимум товарной продукции в денежном выражении.

Вариантные решения

Предусмотреть полное использование того производственного ресурса, который не является дефицитным

Вариант 6

Определить рациональное сочетание посевов ржи, пшеницы и гречихи. Для их возделывания выделяется 800 га пашни, 12000 чел.-дней трудовых ресурсов и 1200 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Рожь	Пшеница	Гречиха
Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га	1,6	1,4	0,8

Критерий оптимальности – максимум производства зерна.

Вариантные решения

Ввести в план посевы культуры, которая получилась невыгодной, добавив в модель 4-е ограничение

Вариант 7

Определить рациональное сочетание посевов пшеницы, ячменя и проса. Для их возделывания выделяется 2000 га пашни, 25000 чел.-дней трудовых ресурсов и 2600 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Пшеница	Ячмень	Просо
Затраты труда, чел.-дн. Норма внесения удобрений Урожайность, ц/га	1,4	1,2	1,0

Критерий оптимальности – максимум производства зерна.

Вариантные решения

Изменить коэффициент целевой функции при переменной таким образом, чтобы культура стала выгодной

Вариант 8

Определить рациональное сочетание посевов ячменя, овса и гречихи. Для их возделывания выделяется 1200 га пашни. 14000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Ячмень	Овёс	Гречиха
Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га	1,2	1,0	0,8

Критерий оптимальности – максимум производства зерна.

Вариантные решения

Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.

Вариант 9

Определить рациональное сочетание посевов ржи, ячменя и овса. Для их возделывания выделяется 1500 га пашни, 22000 чел.-дней трудовых ресурсов и 2000 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.

Показатели	Рожь	Ячмень	Овёс
Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га	1,6	1,2	1,0

Критерий оптимальности – максимум производства зерна.

Вариантные решения

Увеличить объём любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным

Лабораторная работа №3