Фгоу впо «курганская государственная
ФГОУ ВПО «КУРГАНСКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ ИМЕНИ Т.С. МАЛЬЦЕВА»
Кафедра вычислительной техники и информатики
Методические указания для лабораторных работ
по дисциплине
«Моделирование социально-экономических систем»
(для студентов 4 курса экономического факультета отделения бухгалтерский учёт анализ и аудит)
Лесниково-2010
Лабораторная работа №1
«Решение задач линейного программирования
С использованием Microsoft Excel»
ЦЕЛЬ РАБОТЫ
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Изучите инструкцию по решению задач ЛП в табличном редакторе Microsoft Excel. Выполните на компьютере все приведенные ниже примеры. Покажите работу преподавателю.
После изучения всех методических указаний и примеров для модели ЛП, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю. Защитите лабораторную работу.
ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;
b) ввести исходные данные в экранную форму:
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения"):
· целевую ячейку,
· направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения"):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношениямежду правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения");
b) запустить задачу на решение (в окне "Поиск решения");
c) выбрать формат вывода решения (в окне "Результаты поиска решения").
Одноиндексные задачи ЛП
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
 | (1.1) |
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.

Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке F6)
В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 (  ), C3 (
), C3 (  ), D3 (
), D3 (  ), E3 (
), E3 (  ), коэффициентам ЦФ соответствуют ячейки B6 (
), коэффициентам ЦФ соответствуют ячейки B6 (  130,5), C6 (
130,5), C6 (  20), D6 (
20), D6 (  56), E6 (
56), E6 (  87,8), правым частям ограничений соответствуют ячейки H10 (
87,8), правым частям ограничений соответствуют ячейки H10 (  756), H11 (
756), H11 (  450), H12 (
450), H12 (  89) и т.д.
89) и т.д.
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
 . . | (1.2) |
Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
 . . | (1.3) |
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter"
| =СУММПРОИЗВ(B$3:E$3;B6:E6), | (1.4) |
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).

Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул
(курсор в ячейке F6)
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки "  "на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
"на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
· курсор в поле F6;
· нажав кнопку "  ",вызовите окно"Мастер функций – шаг 1 из 2";
",вызовите окно"Мастер функций – шаг 1 из 2";
· выберите в окне "Категория"категорию "Математические";
· в окне "Функция"выберитефункциюСУММПРОИЗВ;
· в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6(рис.1.3);
· после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

Рис.1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций"
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 –1-е ограничение; B11, C11, D11, E11– 2-е ограничение и B12, C12, D12, E12 –3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.
Таблица 1.1 - Формулы, описывающие ограничения модели (1.1)
| Левая часть ограничения | Формула Excel |
 или или  | =СУММПРОИЗВ(B$3:E$3;B10:E10) |
 или или  | =СУММПРОИЗВ(B$3:E$3;B11:E11) |
 или или  | =СУММПРОИЗВ(B$3:E$3;B12:E12) |
Как видно из табл.1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
· поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами "Ctrl-Insert");
· помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11иF12,и вставлять в эти поля содержимое буфера (клавишами "Shift-Insert") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
· на экране в полях F10,F11 и F12 появится 0 (нулевое значение) (см. рис.1.2).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне "Поиск решения". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис.1.8).
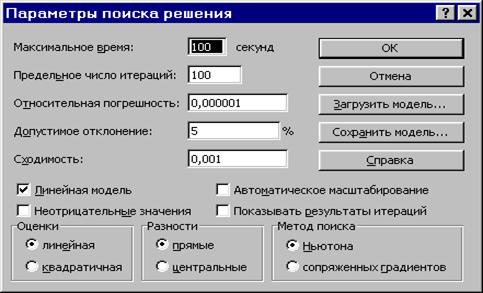
Рис.1.8. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр"Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр"Предельное число итераций"служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр"Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр"Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр"Сходимость" применяется только при решении нелинейных задач.
Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "OK".
Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
После запуска на решение задачи ЛП на экране появляется окно "Результаты поиска решения"с одним из сообщений, представленных на рис.1.9, 1.10 и 1.11.
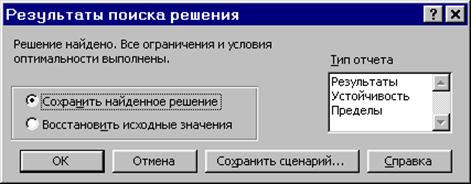
Рис.1.9. Сообщение об успешном решении задачи
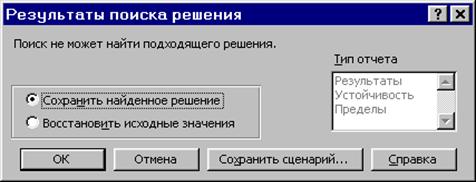
Рис.1.10. Сообщение при несовместной системе ограничений задачи
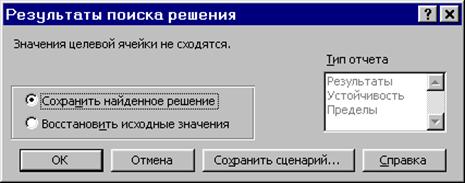
Рис.1.11. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда сообщения, представленные на рис.1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне "Результаты поиска решения"представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис.1.12).
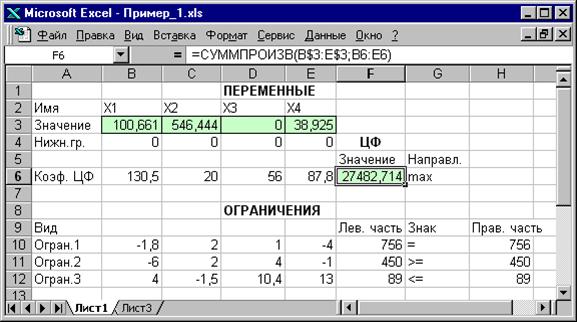
Рис.1.12. Экранная форма задачи (1.1) после получения решения
Двухиндексные задачи ЛП
Двухиндексные задачи ЛП вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл.1.2).
Таблица 1.2
Исходные данные транспортной задачи
| Тарифы, руб./шт. | 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. |
| 1-й склад | ||||
| 2-й склад | ||||
| 3-й склад | ||||
| 4-й склад | ||||
| Потребности, шт. |
Целевая функция и ограничения данной задачи имеют вид
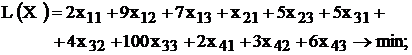 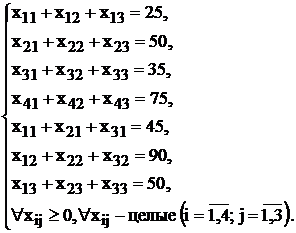 | (1.5) |
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис.1.15, 1.16, 1.17 и в табл.1.3.
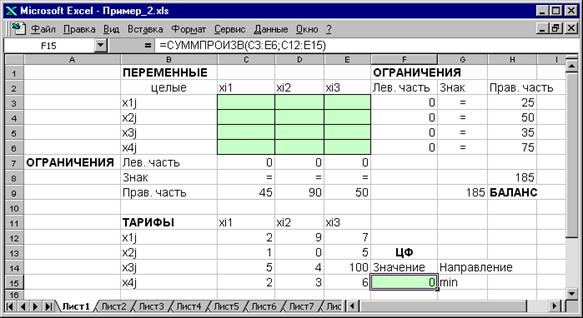
Рис.1.15. Экранная форма двухиндексной задачи (1.5)
(курсор в целевой ячейке F15)
Таблица 1.3
Формулы экранной формы задачи (1.5)
| Объект математической модели | Выражение в Excel |
| Переменные задачи | C3:E6 |
| Формула в целевой ячейке F15 | =СУММПРОИЗВ(C3:E6;C12:E15) |
| Ограничения по строкам в ячейках F3, F4, F5, F6 | =СУММ(C3:E3) =СУММ(C4:E4) =СУММ(C5:E5) =СУММ(C6:E6) |
| Ограничения по столбцам в ячейках С7, D7, E7 | =СУММ(C3:C6) =СУММ(D3:D6) =СУММ(E3:E6) |
| Суммарные запасы и потребности в ячейках H8, G9 | =СУММ(H3:H6) =СУММ(C9:E9) |
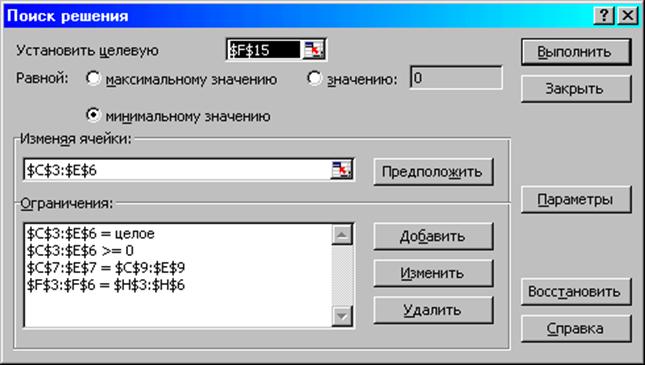
Рис.1.16. Ограничения и граничные условия задачи (1.5)
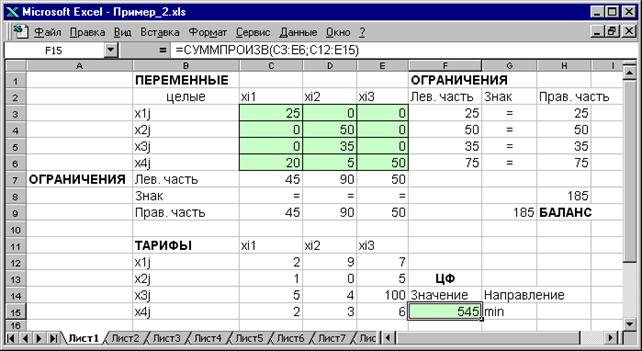
Рис.1.17. Экранная форма после получения решения задачи (1.5)
(курсор в целевой ячейке F15)
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Каковы основные этапы решения задач ЛП в MS Excel?
2. Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений?
3. В чем смысл использования символа $ в формулах MS Excel?
4. В чем различие использования в формулах MS Excel символов ; и :?
5. Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения?
6. Каким образом в MS Excel задается направление оптимизации ЦФ?
7. Какие ячейки экранной формы выполняют иллюстративную функцию, а какие необходимы для решения задачи?
8. Как наглядно отобразить в экранной форме ячейки, используемые в конкретной формуле, с целью проверки ее правильности?
9. Поясните общий порядок работы с окном "Поиск решения".
10. Каким образом можно изменять, добавлять, удалять ограничения в окне "Поиск решения"?
11. Какие сообщения выдаются в MS Excel в случаях: успешного решения задачи ЛП; несовместности системы ограничений задачи; неограниченности ЦФ?
12.Объясните смысл параметров, задаваемых в окне "Параметры поиска решения".
13. Каковы особенности решения в MS Excel целочисленных задач ЛП?
14. Каковы особенности решения в MS Excel двухиндексных задач ЛП?
15. Каковы особенности решения в MS Excel задач ЛП с булевыми переменными?
ВАРИАНТЫ
Используя MS Excel, найти решение для модели ЛП (табл.1.5) в двух вариантах:
1) нецелочисленном;
2) целочисленном.
Показать решение преподавателю и защитить лабораторную работу.
Таблица 1.5 - Варианты задач к лабораторной работе №1
| № варианта | Математическая модель |
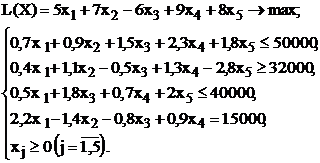 | |
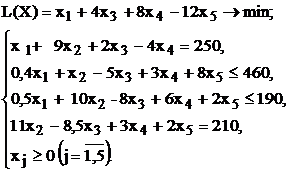 |
| № варианта | Математическая модель |
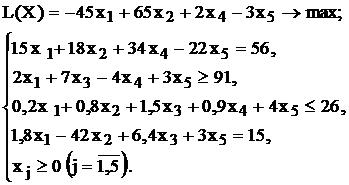 | |
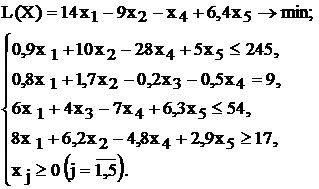 | |
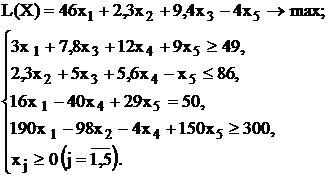 | |
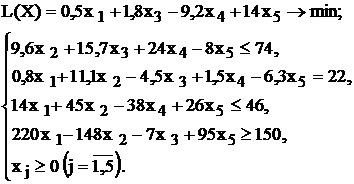 | |
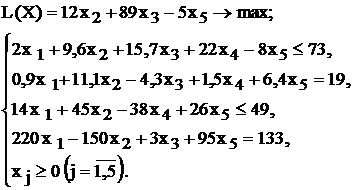 |
| № варианта | Математическая модель |
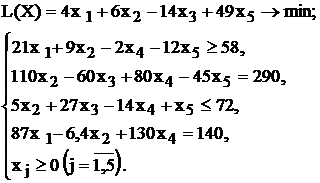 | |
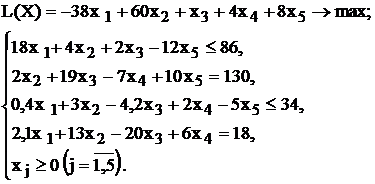 | |
 | |
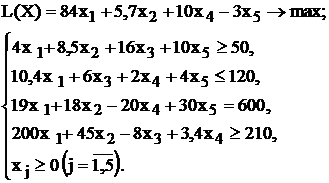 | |
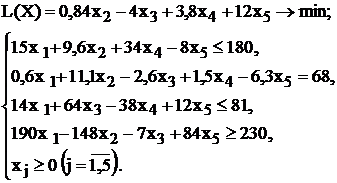 |
Лабораторная работа №2
«РЕШЕНИЕ ЗАДАЧ СИМПЛЕКСНЫМ МЕТОДОМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ»
ЦЕЛЬ РАБОТЫ
1. Построить экономико-математическую модель задачи.
2. Матрицу задачи ввести в компьютер.
3. Выполнить необходимые настройки и решить задачу.
4. Проанализировать полученное решение.
5. Выполнить вариантные решения по перечисленным ниже пунктам.
Условие задачи.
Для выращивания зерновых культур (пшеницы, ячменя и гороха) выделяется 800 га пашни, 12000 чел.-ч трудовых ресурсов и 1300 ц минеральных удобрений. Технико-экономические коэффициенты в расчёте на 1 га посева каждой культуры приведены в таблице.
| Показатели | Пшеница | Ячмень | Горох |
| Затраты труда, чел.-ч | |||
| Норма внесения удобрений, ц | 1,4 | 1,2 | 0,9 |
| Урожайность, ц. |
Критерий оптимальности – максимум производства зерна.
Вариантные решения
Примечание. Для каждого варианта сохранить отчёты по результатам и устойчивости, затем вернутся к первоначальному условию.
1. Ввести в план посевы культуры, которая получалась невыгодной, добавив в модель 4-е ограничение.
2. Изменить коэффициент целевой функции при этой переменной таким образом, чтобы культура стала выгодной.
3. Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.
4. Увеличить объем любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным.
5. Предусмотреть полное использование того производственного ресурса, который не является дефицитным.
6. В том случае, когда в последнем варианте не получается оптимального решения, определить, какими должны быть объёмы производственных ресурсов (дефицитных в первоначальном решении), чтобы все три ресурса использовались полностью.
Все необходимые изменения для получения нового варианта решения задачи делаются в исходной матрице. В соответствии с ними вносятся изменения в окне «Поиск решения» и задача решается повторно. По окончании решения в типовом отчёте по результатам можно будет сравнить новое решение (столбец «Результат») с предыдущим (столбец «Исходно»).
Изменение коэффициента при переменной или объёма ограничения. Для этого достаточно исправить коэффициент при переменной или объём ограничения в исходной матрице и повторно решить задачу, не внося исправлений в настройки в окне «Поиск решения».
Добавление ограничения (ограничений) в матрицу. Ограничения вводятся после последнего, имеющегося в матрице. В ячейку по столбцу «Значение по решению» копируется формула из предыдущей строки, после чего в окне «Поиск решения» добавляется условие на эти ограничения и задача решается повторно.
Удаление лишних ограничений. Из матрицы удаляются все лишние строки, после чего соответствующие условия удаляются в окне «Поиск решения» и задача решается повторно.
Ввод в оптимальный план переменной, не вошедшей в него (получившей нулевое значение) или изменение значения какой-либо переменной. Для этого в матрицу добавляется ограничение на соответствующую переменную.
Например, нужно, чтобы площадь посева ячменя в нашей задаче была равна 280 га. Ограничение на эту переменную запишется следующим образом: Х2=280. Это ограничение вводится в матрицу под номером 5.
2.1.Варианты для самостоятельной работы
Вариант 1
Определить рациональное сочетание посевов ржи, пшеницы и гречихи. Для их возделывания выделяется 800 га пашни, 12000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Рожь | Пшеница | Гречиха |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р. | 1,6 | 1,4 | 0,8 |
Критерий оптимальности – максимум товарной продукции в денежном выражении
Вариантные решения
Ввести в план посевы культуры, которая получилась невыгодной, добавив в модель 4-е ограничение
Вариант 2
Определить рациональное сочетание посевов пшеницы, ячменя и проса. Для их возделывания выделяется 1000 га пашни, 13000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Пшеница | Ячмень | Просо |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р. | 1,4 | 1,2 | 1,0 |
Критерий оптимальности – максимум товарной продукции в денежном выражении.
Вариантные решения
Изменить коэффициент целевой функции при переменной таким образом, чтобы культура стала выгодной
Вариант 3
Определить рациональное сочетание посевов ячменя, овса и гречихи. Для их возделывания выделяется 1200 га пашни. 15000 чел.-дней трудовых ресурсов и 1200 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Ячмень | Овёс | Гречиха |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р. | 1,2 | 1,0 | 0,8 |
Критерий оптимальности – максимум товарной продукции в денежном выражении.
Вариантные решения
Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.
Вариант 4
Определить рациональное сочетание посевов ржи, ячменя и овса. Для их возделывания выделяется 1500 га пашни, 23000 чел.-дней трудовых ресурсов и 1900 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Рожь | Ячмень | Овёс |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р. | 1,6 | 1,2 | 1,0 |
Критерий оптимальности – максимум товарной продукции в денежном выражении
Вариантные решения
Увеличить объём любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным
Вариант 5
Определить рациональное сочетание посевов пшеницы, ячменя и овса. Для их возделывания выделяется 2000 га пашни, 25000 чел.-дней трудовых ресурсов и 2400 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Пшеница | Ячмень | Овёс |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Стоимость товарной продукции, р. | 1,4 | 1,2 | 0,8 |
Критерий оптимальности – максимум товарной продукции в денежном выражении.
Вариантные решения
Предусмотреть полное использование того производственного ресурса, который не является дефицитным
Вариант 6
Определить рациональное сочетание посевов ржи, пшеницы и гречихи. Для их возделывания выделяется 800 га пашни, 12000 чел.-дней трудовых ресурсов и 1200 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Рожь | Пшеница | Гречиха |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га | 1,6 | 1,4 | 0,8 |
Критерий оптимальности – максимум производства зерна.
Вариантные решения
Ввести в план посевы культуры, которая получилась невыгодной, добавив в модель 4-е ограничение
Вариант 7
Определить рациональное сочетание посевов пшеницы, ячменя и проса. Для их возделывания выделяется 2000 га пашни, 25000 чел.-дней трудовых ресурсов и 2600 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Пшеница | Ячмень | Просо |
| Затраты труда, чел.-дн. Норма внесения удобрений Урожайность, ц/га | 1,4 | 1,2 | 1,0 |
Критерий оптимальности – максимум производства зерна.
Вариантные решения
Изменить коэффициент целевой функции при переменной таким образом, чтобы культура стала выгодной
Вариант 8
Определить рациональное сочетание посевов ячменя, овса и гречихи. Для их возделывания выделяется 1200 га пашни. 14000 чел.-дней трудовых ресурсов и 1300 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Ячмень | Овёс | Гречиха |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га | 1,2 | 1,0 | 0,8 |
Критерий оптимальности – максимум производства зерна.
Вариантные решения
Добавить в план 4-ю культуру. Коэффициенты для неё задать произвольно.
Вариант 9
Определить рациональное сочетание посевов ржи, ячменя и овса. Для их возделывания выделяется 1500 га пашни, 22000 чел.-дней трудовых ресурсов и 2000 ц минеральных удобрений. Затраты производственных ресурсов на 1 га посева каждой культуры и выход продукции приведены в таблице.
| Показатели | Рожь | Ячмень | Овёс |
| Затраты труда, чел.-дн. Норма внесения удобрений, ц Урожайность, ц/га | 1,6 | 1,2 | 1,0 |
Критерий оптимальности – максимум производства зерна.
Вариантные решения
Увеличить объём любого из дефицитных ресурсов настолько, чтобы он перестал быть дефицитным
Лабораторная работа №3
Условие задачи
Необходимо составить рацион на стойловый период для коров с живой массой 450 кг, удоем 8 кг в сутки, жирностью молока 3,8%.
Для коров с указанной живой массой и продуктивностью суточная норма потребности в питательных веществах следующая: не менее 16 кормовых единиц, 1800г переваримого протеина, 110г кальция, 80г фосфора, 670 мг каротина и не более 20 кг сухого вещества.
Соотношение между содержанием кальция и фосфора в рационе должно быть не более чем 2,5:1.
Пределы содержания отдельных видов и групп кормов в рационе представлены следующим образом:
концентраты 10 - 30 % грубые корма 25 - 35 % ,
силос 35 - 60 % корнеплоды 10 - 20 %
Таблица 1 – Характеристика имеющихся в хозяйстве кормов по содержанию питательных веществ и себестоимости
| Наименование кормов | Содержится в 1 кг корма | Себестоимость1 кг, р. | |||||
| кормовых единиц, кг | переваримого протеина, г | кальция, г | фосфора, г | каротина, мг | сухого вещества, кг | ||
| Ячмень | 1,03 | 1,2 | 3,3 | 0,78 | 3,0 | ||
| Овёс | 1,7 | 3,3 | - | 0,87 | 3,1 | ||
| Горох | 1,17 | 1,7 | 4,2 | 0,87 | 6,3 | ||
| Солома пшеничная | 0,20 | 1,4 | 0,8 | 0,80 | 0,4 | ||
| Солома овсяная | 0,31 | 4,3 | 1,0 | 0,80 | 0,4 | ||
| Сено люцерновое | 0,49 | 17,7 | 2,2 | 0,85 | 2,4 | ||
| Сено суданки | 0,52 | 5,7 | 2,3 | 0,85 | 3,1 | ||
| Силос кукурузный | 0,20 | 1,5 | 0,5 | 0,26 | 0,8 | ||
| Сахарная свёкла | 0,26 | 0,5 | 0,5 | - | 0,24 | 0,5 | |
| Кормовые корнеплоды | 0,12 | 0,4 | 0,4 | - | 0,12 | 1,6 | |
| Кормовой преципитат | - | - | - | - | 5,1 |
Критерий оптимальности - минимальная себестоимость рациона.
Таблица 2 - Матрица задачи по оптимизации рациона кормления животных
| Ограничения | Х1 Ячмень | … | Х14 Содерж. фосфора в рационе | Тип ограничения | Объём ограничения |
| 1. Общая питательность | |||||
| 2. Корм. ед. | |||||
| 3. Перев. протеин, г | |||||
| … | |||||
| 18. Соотношение между Са и Р | |||||
| Себестоимость, р. | → | min |
Таблица 3 - Представление матрицы в модуле «Поиск решения» в MS Excel
| Наименование переменных | Х1 Ячмень | … | Х14 Содерж. фосфора в рационе | Объём ограничения по решению | Тип ограничения | Объём ограничения по условию |
| Значение по решению | ||||||
| Себестоимость, р. | ||||||
| Наименование ограничения | ||||||
| 1. Общая питательность | ||||||
| 2. Корм. ед. | ||||||
| 3. Перев. протеин, г | ||||||
| … | ||||||
| 18. Соотношение между Са и Р |
Таблицы для оформления результатов решения задачи
| Таблица 4 - Содержание кормов в рационе и его себестоимость | |||
| Вид корма | Количество, кг | Себестоимость, усл.ед. | |
| 1 кг корма | всего | ||
| Ячмень | |||
| Солома овсяная | |||
| Сено люцерновое | |||
| Силос | |||
| Сахарная свёкла | |||
| Корм. преципитат | |||
| Итого |
| Таблица 5 - Содержание элементов питания в рационе | |||
| Вид элемента питания | По норме | По решению | Отклонение |
| Кормовые единицы | |||
| Переваримый протеин, г | |||
| Кальций, г | |||
| Фосфор, г | |||
| Каротин, мг | |||
| Сухое вещество, кг |
| Таблица 6 - Структура рациона | ||
| Виды и группы кормов | Структура рациона | |
| корм.ед. | % к итогу | |
| Концентраты | ||
| Грубые | ||
| Силос | ||
| Корнеплоды | ||
| Итого |
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Какова постановка экономико-математической задачи оптимизации рациона кормления скота ?
2. Запишите математическую модель .
3. Перечислите исходные данные .
4. Какова суть каждого из этапов построения модели ?
5 Как можно классифицировать ограничения задачи по их экономическому смыслу?
6 Объясните построения каждого конкретного ограничения задачи .
3.3. Варианты для самостоятельной работы
Задание 1
Необходимо составить рацион кормления для коровы живой массой 450 кг, суточным удоем 12 л. Набор кормов для рациона и содержание питательных элементов в 1 кг корма приведены в таблице.
| Виды кормов | Кормовые единицы, кг | Переваримый протеин, г | Себестоимость, р. |
| Концентраты | 1,17 | ||
| Сено | 0,45 | ||
| Силос | 0,18 | ||
| Сенаж | 0,23 | ||
| Солома | 0,2 |
Суточная потребность в кормовых единицах составляет 11,3 кг, в переваримом протеине - 1270 г, в концентрированных кормах - не менее 2 кг.
Структура рациона (по питательности): концентраты 18-30%
грубые и сенаж 35-50%
силос 25-40%.
Критерий оптимальности - минимум себестоимости рациона.
Задание 2.
Необходимо составить рацион кормления для коровы живой массой 500 кг, суточным удоем 10 л. Набор кормов для рациона и содержание питательных элементов в 1 кг корма приведены в таблице.
Таблица 6 – Виды кормов, их питательность и себестоимость
| Виды кормов | Кормовые единицы, кг | Переваримый протеин, г | Себестоимость, р. |
| Концентраты |
