Перечень литературы и средств обучения

Основная

1. Судоплатов С.В., Овчинникова Е.В., Элементы дискретной математики, М, Инфра – М, 2002.

2. Гаврилов Г.П., Сапоженко А.А., Задачи и упражнения по курсу дискретной математики. М, Наука, 1992.

3. Лавров И.А., Максимова Л.Л., Задачи по теории множеств, математической логике и теории алгоритмов, М, Наука, 1984.

4. Емеличев В.А.және басқалар, Лекции по теории графов, М, Наука, 1990.

5. Р.Грэхем, Д.Кнут, О. Паташник, Конкретная математика, М., Мир, 1998 .

6. Джумадильдаев А.С., Элементы дискретной математики, Учебное пособие, часть 1, Университет Сулеймана Демирели, Алматы, 2004.

7. Судоплатов С.В., Овчинникова Е.В., Элементы дискретной математики, М, Инфра – М, 2002.

8. Новиков Ф. А., Дискретная математика для программистов., СПб, Питер, 2001.

9. Э. Мендельсон. Введение в математическую логику. М.: Наука, 1984.

10. Виноградов И.М., Основы теории чисел, М., Наука, 1972.

11. Емеличев В.А.және басқалар, Лекции по теории графов, М, Наука, 1990.

12. Ершов Ю.Л., Палютин Е.А., Математическая логика. М, Наука,1987.

13. Гаврилов Г.П., Сапоженко А.А., Задачи и упражнения по курсу дискретной математики. М, Наука, 1992.

14. Лавров И.А., Максимова Л.Л., Задачи по теории множеств, математической логике и теории алгоритмов, М, Наука, 1984.

Дополнительная

1. С.В. Яблонский, Введение в дискретную математику, М., Наука, 1979 г.

2. Новиков Ф. А., Дискретная математика для программистов., СПб, Питер,

3. О. Оре, Теория графов , М., Наука, 1985 г.

4. М. Холл, Комбинаторика, М., Мир, 1970 г.

5. Горбатов В. А., Фундаментальные основы дискретной математики. М, Физматлит, 2000.

6. Горбатов В. А., Фундаментальные основы дискретной математики. М, Физматлит, 2000.

7. Яблонский С.В., Введение в дискретную математику. М, Наука, 1986.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

Казахстанский инженерно-технологический университет

Кафедра «Вычислительная техника, автоматизация и телекоммуникация»

«Утверждаю»

Проректор поУНиВ работе

_______к.ф.н.Сарсенбекова Г.А.

“ ____” _____________ 2016г

УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ (SYLLABUS)

PUNP «Применение удобрения нового поколения»

для специальности магистратуры 6М080900 – Плодоовощеводство

2 кредита

Форма обучения - дневная

Количество кредита – 2

Курс - 1

Семестр - 2

Лекции - 15 часов

Практические занятия - 15 часов

Лабораторные занятия - 30 часов

СРСП - 30 часов

СРС - 90 часов

Вид контроля: Экзамен

Всего: 150 часов

Алматы 2016

Учебная программа дисциплины (syllabus) составлена по дисциплине «Применение удобрения нового поколения» на основании типовой учебной программыдля специальности магистратуры 6М080900 – Плодоовощеводство

Рассмотрена и одобрена на заседании кафедры «Технологии, оборудования и стандартизации»

«___23__»_августа 2016 г. Протокол № _1___

Зав. кафедрой ТоиС ______________ Каржаубаев К.Е.

Составитель ______________ Султанова З.К.

Рассмотрена и утверждена на заседании учебно-методического совета протокол № 1 от 24.08.2016

© Казахстанский инженерно-технологический университет, 2016

УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИН (SYLLABUS)

1.Данные о преподавателе:

Султанова Зиада Клычбаевна - преподаватель кафедры «Технологии, оборудования и стандартизации»2 корпус, кафедра ТОиС (№ 307 ауд.)

Контакты: 87017264955

2. Название дисциплины–«Применение удобрения нового поколения».

3. Время и место проведения аудиторных занятий курса указано в расписании учебных занятий, график консультаций СРСП размещен на информационной доске университета и кафедры ТОиС (каб. 313)

4. Пререквизиты и постреквизиты учебной дисциплины

Пререквизиты

биология, химия, технология, математика, экономика

Постреквизиты

Применение удобрения нового поколения

5 Характеристика учебной дисциплины

5.1 Краткая информация о дисциплине.

5.4.Содержание дисциплины

5. 4.1 Теоретическая подготовка (30 час.)

Таблица 1

№ п/п	Наименование тем	Кол-во часов
	Множества. Функции и отношения. Тождества алгебры множеств.
	Мощность множества. Конечные и бесконечные множества. Отношения. Отношения и основные операции над ними.
	Специальные бинарные отношения. Порядковые отношения.
	Отношения эквивалентности. Теорема о разделении. Функции. Функции и операции над ними.
	Инъекция, сюръекция, биекция. Правила вычисления. Правило Дирихле.
	Правило входа и выхода. Замена. Размещение и подбор. Бином Ньютона. Треугольник Паскаля.
	Инъекция, сюръекция и биекция в конечных множествах. Метод математической индукции. Рекуррентные отношения.
	Операция деления на целочисленных кольцах. Простые и сложные числа. Сравние целых чисел по модулю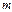
	Китайская теорема об остатках. Мультипликативные функции.
	Теоремы Эйлера и Ферма. Последовательные дроби.
	Решение уравнении в целых числах. Шифрование. Криптосистема с открытым ключом.
	Определение графов. Мультиграф. Изоморфизм графов.
	Внутренние графы. Операции применяемые над графами.
	Связь графов. Эйлеровые графы. Плоские графы. Ветки и леса.
	Машина Тьюринга. Программы копирования и замены.
	Всего

5. 4.2 Практическая подготовка

Таблица 2

Тематика практических занятий (15)

№ п/п	Наименование тем	Кол-во часов
	Тождества алгебры множеств. Множества и основные операции над ними.
	Отношения и основные операции над ними.
	Порядковые отношения.
	Эквивалентные отношения.
	Инъекция, сюръекция и биекция. Правила вычисления. Правило Дирихле.
	Правило входа и выхода. Размещение и подбор.
	Рекуррентные отношения.
	Числа Фиббоначи. Производящие функции. Целые числа и операции деления.
	Мультипликативные функции.
	Последовательные дроби. Приближенные дроби.
	Решение уравнения в целых числах. Нахождение простых чисел в конечных множествах
	Изоморфизм графов.
	Операции применяемые над графами.
	Эйлеровые графы. Плоские графы. Раскраска графов.
	Программы вычисления функций простых чисел.
	Всего

5.4.3 Наименование тем самостоятельной работы студентов с преподавателем(СРСП),их содержание и объем в часах

Таблица 3

График СРС, СРСП

недели	Номер занятий по syllabus	СРС	в том числе СРСП
Тема и вид задания (с указанием страниц литературы)	Срок выдачи и приема задания (нед)	Тема и вид задания (с указанием страниц литературы)	Срок выдачи и приема задания (нед)
1-3	СРСП - 1	Парадокс Рассела (Дж. 3-8 с., Суд. 9-15 с., Мен.) Принцип максимума. Аксиома выбора (Мен.)			Парадокс Рассела (Дж. 3-8 с., Суд. 9-15 с., Мен.) Принцип максимума. Аксиома выбора (Мен.)
3-4	СРСП - 2	Обобщенные правила сложения и умножения (Дж. 25-32, Суд. 164-165, Нов. 151-153)			Обобщенные правила сложения и умножения (Дж. 25-32, Суд. 164-165, Нов. 151-153)
4-5	СРСП - 3	Повторение, рамещение и подбор. Суд. 157-164, Нов. 135-141			Повторение, рамещение и подбор. Суд. 157-164, Нов. 135-141
5-6	СРСП - 4	Производящие функции и их свойства. (Дж. 38-45, 53-55, Суд. 22-25, 165-168,86-91, Вин.7-18)			Производящие функции и их свойства. (Дж. 38-45, 53-55, Суд. 22-25, 165-168,86-91, Вин.7-18)
6-7	СРСП - 5	Мультипликативность функции Мебиуса. (Дж.58-60,64-67,Вин.54-57,26-32, Суд. 91-98)			Мультипликативность функции Мебиуса. (Дж.58-60,64-67,Вин.54-57,26-32, Суд. 91-98)
7-8	СРСП - 6	Мультипликативность функции Эйлера. (Дж. 58-69, Вин. 54-57, 26-32, Суд. 91-98)			Мультипликативность функции Эйлера. (Дж. 58-69, Вин. 54-57, 26-32, Суд. 91-98)
8-9	СРСП - 7	Решето Эратосфена. Компьютерное тестирование для определении простых чисел. (Дж. 72-78, Нов. 180-183, 185-188)			Решето Эратосфена. Компьютерное тестирование для определении простых чисел. )Дж. 72-78, Нов. 180-183, 185-188)
9-10	СРСП - 8	Описание отношений с помощью графов. (Суд.107-113, Нов.189-197)			Описание отношений с помощью графов. (Суд.107-113, Нов.189-197)
10-11	СРСП - 9	Раскраска графов. (Суд. 150-152, 132-135, 114-117, Нов. 197-199, 234-238, Суд. 129-131, 152-154, Нов. 263-264)			Раскраска графов. (Суд. 150-152, 132-135, 114-117, Нов. 197-199, 234-238, Суд. 129-131, 152-154, Нов. 263-264)
11-14	СРСП - 10	Задача о мостах Кенисберга			Задача о мостах Кенисберга

Самостоятельная работа студентов (СРС) и (СРСП) проводится в соответствии с расписанием .

5.5 План изучения дисциплины.

№ п/п	Наименование темы учебной дисциплины	Содержание раздела темы в дидактических единицах
	Комбинаторика конечных множеств.	Множества и операции над ними. Тождества алгебры множеств. Принципы суммы и произведения. Характеристическая функция подмножества. Принцип включения и исключения. Принцип Дирихле и его применения. Отображения и и виды отображения. Бинарные отношения и операции над ними. Бином Ньютона. Свойства биномиальных коэффициенттов.
	Реккурентные соотношения. Производящие функции.	Рекурентные соотношения. Алгебра бесконечных последовательностей. Числа Фибоначчи и Каталана. Теорема Юнга. Числа Белла и Мерсенна. Производящие функции и операции над ними. Элементарные производящие функции и определямые ими ряды. Произведение производящих функции. Операция свертки.
	Элементы теории графов.	Понятие графа. Графы, сети, коды. Виды графов. Представление графов. Эйлеровы и гамильтоновы графы. Деревья. Хроматическое число графов. Теорема Эйлера о планарных графах. Теорема Понтрягина-Куратовского.
	Алгоритмы теории чисел.	Кольцо целых чисел. Теорема о делении с остатком. Алгоритм Эвклида. Простые и составные числа. Основная теорема арифметики. Взаимно простые числа и их свойства. Теоремы Ферма и Эйлера. Китайская теорема об остатках.
	Конечные поля.	Сравнения и их свойства. Кольцо вычетов. Необходимое и достаточное условие, что кольцо вычетов является полем. Построение конечных полей. Алгоритм нахождения примитивного элемента поля.
	Стандартные задачи криптографии.	Исторические шифросистемы. Шифры замены и подстановки. Шифросистемы с открытым клюом и алгоритмы дешифрования шифров с открытым ключом.
	Введение в теорию кодирования.	Обзор схем кодированя. Неравенство Макмиллана. Алгоритмы сжатия данных, алгоритм Лемпела-Зива.
	Алгебра логики.	Булевы алгебры. Булевы функции. Лемма о числе булевых функции. Равносильные преобразование булевых функции. СДНФ и СКНФ. Полиномы Жегалкина. Теорема Жегалкина. Основные классы булевых функции. Полные системы логических связок.
	Элементы математической логики.	Высказывания, таблица истинности. формул. Нормальные формы. Понятия предиката и терма. Кванторы и формулы. Понятие модели. Выполнимость формулы в модели. Эквивалентность формул. Универсальные и хорновы формулы. Теорема Эрбрана, сколемизация. Понятие алгоритма. Машины Тъюринга. Методы математических доказательств.