Элементы математической логики.

Высказывания, таблица истинности. формул. Нормальные формы. Понятия предиката и терма. Кванторы и формулы. Понятие модели. Выполнимость формулы в модели. Эквивалентность формул. Универсальные и хорновы формулы. Теорема Эрбрана, сколемизация. Понятие алгоритма. Машины Тъюринга. Методы математических доказательств.

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ СЕМИНАРСКИХ ЗАНЯТИЙ

1. Множества и операции над ними.

2. Принципы суммы и произведения.

3. Принцип включения и исключения. Характеристическая функция подмножества.

4. Принцип Дирихле и его применения.

5. Бинарные отношения и операции над ними.

6. Бином Ньютона. Свойства биномиальных коэффициенттов.

7. Рекурентные соотношения. Числа Фибоначчи и Каталана.

8. Элементарные производящие функции и определямые ими ряды.

9. Произведение производящих функции. Операция свертки.

10. Представление графов. Эйлеровы и гамильтоновы графы. Деревья.

11. Хроматическое число графов. Применения теоремы Эйлера о планарном графе.

12. Кольцо целых чисел. Кольцо вычетов. Сравнения.

13. Малая теорема Ферма. Теорема Эйлера.

14. Китайская теорема об остатках.

15. Построение полиномов Жегалкина.

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬОЙ РАБОТЫ СТУДЕНТОВ

1. Теорема Эрдеша-Шекереша.

2. Нахождение производящей функции для ряда Фибоначчи.

3. Нахождение производящей функции для ряда Каталана.

4. Делители нуля, нильпотентные и обратимые элементы в кольце вычетов. Идеалы и гомомрфизмы.

5. Решение систем сравнении первой степени.

6. Построение полей Галуа. Вычисления в полях Галуа.

7. Примеры задач криптографии с открытым ключом.

8. Примеры задач теории кодирования.

9. Линейно реккурентные соотношения.

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ С ПРЕПОДАВАТЕЛЕМ

1. Применения теоремы о разбиении.

2. Перестановки, размещения и сочетани.

3. ТеоремаЛагранжа для конечных групп.

4. Классические алгебраические системы.

5. Конечные группы.

6. Построение конечных полей.

7. Вычисления на конечных полях.

8. Подполя поля Галуа.

9. Алгоритмы нахождения примитивного элемента конечного поля.

Министерство образования и науки Республики Казахстан

Казахстанский инженерно-технологический университет

КАФЕДРА «ТЕХНОЛОГИИ, ОБОРУДОВАНИЯ И СТАНДАРТИЗАЦИИ»

«Утверждаю»

Проректор поУНиВ работе

_______к.ф.н.Сарсенбекова Г.А.

“ ____” _____________ 2017г

РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

PUNP «Применение удобрения нового поколения»

для специальности магистратуры 6М080900 – «Плодоовощеводство»

Форма обучения - дневная

Количество кредита – 2

Курс - 1

Семестр - 2

Лекции - 15 часов

Практические занятия -15часов

СРСП - 30 часов

СРС - 30 часов

Вид контроля: Экзамен

Всего:90 часов

Алматы 2016

Рабочая учебная программа дисциплины (syllabus) составлена по дисциплине «Применение удобрения нового поколения» на основании типовой учебной программы для специальности для специальности магистратуры 6М080900 – Плодоовощеводство

Рассмотрена и одобрена на заседании кафедры «Технологии, оборудования и стандартизации»

«___23__»_августа2016г. Протокол № _1___

Зав. кафедрой ТОиС ______________ Каржаубаев К.Е.

Составитель ______________ Султанова З.К.

Рассмотрена и утверждена на заседании учебно-методического совета протокол № 1 от 24.08.2016

© Казахстанский инженерно-технологический университет, 2016

Тематический план

Наименование темы	Количество академических часов
Лекций	Практические занятия	Лабораторные занятия	СРО(из них)
СРСП	СРС
Множества. Функции и отношения. Тождества алгебры множеств.
Мощность множества. Конечные и бесконечные множества. Отношения. Отношения и основные операции над ними.
Специальные бинарные отношения. Порядковые отношения.
Отношения эквивалентности. Теорема о разделении. Функции. Функции и операции над ними.
Инъекция, сюръекция, биекция. Правила вычисления. Правило Дирихле.
Правило входа и выхода. Замена. Размещение и подбор. Бином Ньютона. Треугольник Паскаля.
Инъекция, сюръекция и биекция в конечных множествах. Метод математической индукции. Рекуррентные отношения.
Операция деления на целочисленных кольцах. Простые и сложные числа. Сравние целых чисел по модулю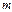
Китайская теорема об остатках. Мультипликативные функции.
Теоремы Эйлера и Ферма. Последовательные дроби.
Решение уравнении в целых числах. Шифрование. Криптосистема с открытым ключом.
Определение графов. Мультиграф. Изоморфизм графов.
Внутренние графы. Операции применяемые над графами.
Связь графов. Эйлеровые графы. Плоские графы. Ветки и леса.
Машина Тьюринга. Программы копирования и замены.
Всего: