Квантово-механическая модель строения атома

В основе современной теории строения атома лежат следующие основные положения:

1. ЭЛЕКТРОН ИМЕЕТ ДВОЙСТВЕНУЮ (корпускулярно-волновую) ПРИРОДУ.

Электрон, как и другие элементарные частицы (протон, нейтрон), обладает определенной массой и зарядом, т.е. ведет себя как частица. В то же время, движущийся электрон проявляет волновые свойства, например характеризуется способностью к дифракции (рассеяние световых лучей) и интерференции (наложение световых волн). Для любой элементарной частицы справедливо уравнение (Луи де Бройль), связывающее параметры волны и частицы

,

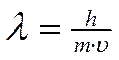где λ – длина волны электрона, h - постоянная Планка, m – масса электрона, υ – скорость движения электрона.

2. ДЛЯ ЭЛЕКТРОНА НЕВОЗМОЖНО ОДНОВРЕМЕННО ТОЧНО ИЗМЕРИТЬ КООРДИНАТУ И СКОРОСТЬ.

В силу наличия у микрочастиц волновых свойств невозможно в каждый момент времени точно фиксировать их положение в пространстве и определять с любой точностью скорость их движения. Чем точнее мы измеряем один параметр, тем больше неопределенность в другом. Принцип неопределенности сформулирован Гейзенбергом (1927 г.) и имеет математическое выражение

,

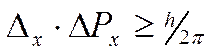где Δ_х – неопределенность положения частицы по оси х, ΔР_х = Δ(m·υ) – неопределенность составляющей импульса по оси х.

Из формулы видно, что чем меньше значение Δ_х , т.е. чем определеннее положение частицы, тем больше ΔР_х, т.е. тем неопределеннее ее импульс. Неопределенность в свойствах микрообъектов проявляется тем в большей степени, чем в большей степени выражена его волновая функция (чем меньше его масса). Поэтому неопределенность в положении электрона значительно больше, чем неопределенность в положении ядра атома.

3. ЭЛЕКТРОН В АТОМЕ НЕ ДВИЖЕТСЯ ПО ОПРЕДЕЛЕННЫМ

ТРАЕКТОРИЯМ, А МОЖЕТ НАХОДИТСЯ В ЛЮБОЙ ЧАСТИ ОКОЛОЯДЕРНОГО ПРОСТРАНСТВА, однако вероятность его нахождения в разных частях этого пространства неодинакова.

Вероятность нахождения электрона в разных местах околоядерного пространства можно определить с помощью уравнения Шредингера

,

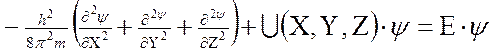где h – постоянная Планка, m – масса электрона, U – потенциальная энергия, Е – полная энергия, ψ – волновая (пси) функция. Первый член уравнения

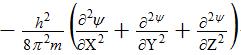
соответствует кинетической энергии частицы (Е_к) с массой m. При короткой записи Е_к описывается оператором Лапласа

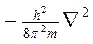
где 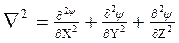- оператор Лапласа.

Упрощенный вид уравнения Шредингера

.

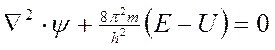Решение этого уравнения связано с большими математическими трудностями. Точное решение оно имеет для атома водорода и для одноэлектронных частиц. Для сложных атомов уравнение Шредингера может быть решено только приблизительно. Решая его находят энергию электрона, а также функцию координат электрона X, Y, Z и времени τ:

.

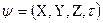Волновая функция ψ представляет собой амплитуду трехмерной электронной волны. Причем она имеет как положительные, так и отрицательные значения. Квадрат модуля волновой функции

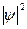
характеризует вероятность нахождения электрона в некотором объеме. Эту величину называют также электронной плотностью. Если в соответствии с уравнением Шредингера получим, что

,

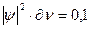где 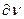- определенный объем, то это значит, что в данном объеме электрон находится 0,1 времени, а 0,9 – в другом месте, т.е. можно утверждать, что электронная плотность в данном объеме равна 0,1. Совокупность мест пространства, где 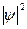имеет максимальное значение называют электронной орбиталью.

Таким образом, электронной орбиталью или электронным облаком называется часть околоядерного пространства, в котором вероятность пребывания электрона максимальна.

Поверхность, охватывающая ядро атома, за пределами которой вероятность пребывания электрона исчезающее мала, называют граничной поверхностью орбитали, которая и передает форму самой орбитали.

4. ЯДРА АТОМОВ СОСТОЯТ ИЗ ПРОТОНОВ И НЕЙТРОНОВ (общее название - нуклоны).

Число протонов в ядре равно порядковому номеру элемента в таблице Д.И. Менделеева, а сумма протонов и нейтронов его атомному числу.

Массовое число (А), заряд ядра (Z), равный числу протонов, и число нейтронов (N) связаны соотношениями: Z = А – N, N = А – Z, А = Z + N.

Атомы с одинаковыми Z, но разными А и N, называют изотопами.

Квантовые числа

Решение уравнения Шредингера позволяет найти волновые функции, при этом выяснено, что для полного определения каждого решения необходимы три целых числа – квантовые числа. Можно сказать, что квантовые числа описывают совокупность движений электронов в атоме.

ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n) определяет общую энергию электрона на данной орбитали и принимает значения n = 1, 2, 3, 4….

Чем больше n, тем больше объем внутреннего пространства атомной орбитали, т.е. растет удаленность электрона от ядра атома. Все электроны с одинаковым значением главного квантового числа образуют электронный слой. Приняты следующие обозначения электронных слоев:

Значение n ……………………………. 1 2 3 4 5 6 7

Обозначение слоя (уровня) ………….. K L M N O P Q.

Зная главное квантовое число можно определить максимальное число электронов, которое может находиться на этом уровне по формуле N_е = 2n².

Возможное число подуровней для каждого электронного уровня численно равно значению n– первый уровень (n = 1) состоит из одного подуровня, второй уровень (n = 2) – из двух и т.д. (табл.3).

ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО ( 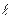), которое иногда называют побочным квантовым числом, определяет форму электронного облака и принимает значения от нуля до n-1. Область электронного уровня, в котором содержатся орбитали определенной формы называется энергетическим подуровнем. Подуровень, содержащий s-орбитали, называется s-подуровнем, р-орбитали - р-подуровнем и т.д. Например, при n = 1, 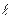= 0 (на первом уровне существуют только s-электроны). При n = 3, 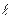= 0, 1, 2 (на третьем уровне содержит 3s-, 3р- и 3d-электроны).

Максимальное число подуровней и орбиталей на энергетических уровнях

Энергетический уровень	Число подуровней	Типы орбиталей	Орбитали,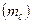
К (n = 1)		1s
L (n = 2)		2s 2p	-1, 0, +1
M (n = 3)		3s 3p 3d	-1, 0, +1 -2, -1, 0, +1, +2
N (n = 4)		4s 4p 4d 4f	-1, 0, +1 -2, -1, 0, +1, +2 -3, -2, -1, 0, +1, +2, +3

Если 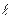= 0, электронное облако имеет сферическую форму (рис. 5);

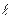= 1 - электронное облако имеет форму симметричной восьмерки (гантель, рис. 6). С ростом численного значения орбитального квантового числа форма электронного облака усложняется .

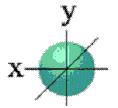
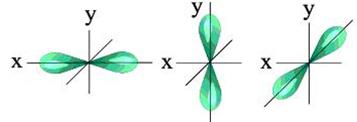
Рис. 6. S-облако. Рис. 7. Р-облака

МАГНИТНОЕ КВАНТОВОЕ ЧИСЛО 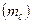характеризует ориентацию данной орбитали в пространстве. Магнитное квантовое число принимает целочисленные значения от - 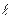до + 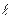, включая ноль. Например,для 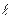= 2, магнитные квантовые числа имеют значения -2, -1, 0, +1, +2, т.е. в данной подоболочке (d-подуровень) существует пять орбиталей. Соответственно на s-подуровне ( 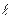= 0) имеется одна орбиталь; на р-подуровне ( 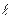= 1) – три орбитали; на f-подуровне – семь орбиталей. Атомную орбиталь обозначают в виде клеточки □. Тогда число орбиталей на соответствующих подуровнях будет равно: s-подуровень - □; р-подуровнь - □□□; d-подуровень - □□□□□; f-подуровнь - □□□□□□□.

Вышерассмотренные квантовые числа полностью характеризуют три определяющих свойства электрона-волны: длину, направление и амплитуду. Однако у электрона-частицы имеется особое свойство, называемое спином. Упрощенно спин можно рассматривать как вращение электрона вокруг собственной оси. Поэтому в теорию строения атома введено еще одно

СПИНОВОЕ КВАНТОВОЕ ЧИСЛО (m_s), которое может принимать два значения в соответствии с двумя возможными направлениями вращения:

m_s = + 1/2 (электрон вращается по часовой стрелке вокруг своей оси и имеет обозначение - ↑), m_s = - 1/2 (электрон вращается против часовой стрелки вокруг своей оси и имеет обозначение - ↓).