Статика. Равновесие тел под действием системы сходящихся сил

ТРЕНИЕ.

Законы трения скольжения.Сила трения скольжения возникает при стремлении двигать одно тело по поверхности другого. Сформулируем законы трения скольжения. Эти законы были установлены в результате первых опытов над трением, проделанных Амонтоном в 1699 г. и более точных экспериментальных исследований, проведенных Кулоном в 1781 г.

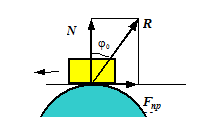
1) При стремлении сдвинуть одно тело по поверхности другого в области соприкосновения тел возникает сила трения, которая может принимать любые значения от нуля до значения 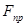, называемого предельной силой трения. Приложенная к телу сила трения направлена в сторону, противоположную той, куда действующие на тело силы стремятся его сдвинуть.

2) Предельная сила трения численно равна произведению коэффициента трения на нормальное давление или нормальную реакцию:

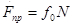Статический коэффициент трения 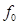- величина безразмерная, он определяется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей.

3) Значение предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся при трении поверхностей.

Из первых двух законов следует, что при равновесии 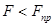или .

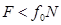Значение силы трения при покое определяется последним неравенством, это значение может быть любым, но не большим, чем 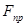. Чему конкретно равна сила трения, можно установить, только решив соответствующую задачу на равновесие с учетом всех действующих сил. Величине 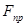сила трения будет равна лишь тогда, когда действующая на тело сдвигающая сила достигает такого значения, что при малейшем ее увеличении тело начинает двигаться

(скользить). Равновесие, при котором сила трения равна 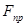, называется предельным равновесием. Приведем значения коэффициента трения 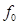для некоторых материалов: дерево по дереву 0,4 – 0,7; металл по металлу

0,15 – 0,25; сталь по льду 0,027.

Замечание. Все изложенное выше относилось к трению скольжения при покое. При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление: 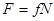. Динамический коэффициент трения скольжения 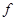также является величиной безразмерной и определяется опытным путем. Значение коэффициента 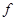зависит не только от материала и состояния поверхностей, но и в некоторой степени от скорости движущихся тел. В большинстве случаев с увеличением скорости коэффициент 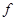сначала несколько убывает, а затем сохраняет почти постоянное значение.

Трение качения. Трением качения называется сила сопротивления, возникающая при качении одного тела по поверхности другого.

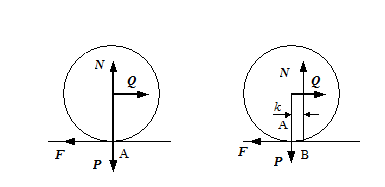Рассмотрим круглый цилиндрический каток радиуса R и веса P , лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу Q , меньшую F_пр. Тогда в точке А возникает сила трения F , численно равная Q , которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию N тоже приложенной в точке А, то она уравновесит силу P , а силы Q и F образуют пару, вызывающую качение цилиндра. При такой схеме качение должно начаться, как видим, под действием сколь угодно малой силы Q .

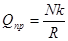В действительности картина будет иной. Вследствие деформации тел под действием сил P и N их касание происходит не в точке, а вдоль некоторой площадки. Под действием силы Q направленной вправо, давление у левого края убывает, а у противоположного - возрастает. При этом нормальная реакция N смещается вправо в некоторую точку В , в сторону действия силы Q . С увеличением Q это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будет действовать пара (Q_пр,F) с моментом Q_прR и уравновешивающая ее пара (N,P) с моментом Nk . Из равенства моментов находим Q_прR=Nk или

Пока Q<Q_пр каток находится в покое; при Q>Q_пр начинается качение.

Входящая в последнюю формулу линейная величина k называется коэффициентом трения качения. Измеряют величину k обычно в сантиметрах. Значение коэффициента k зависит от материала тел и определяется опытным путем. Например, при качении вагонного колеса по рельсу k=0,005 cм, а для шариковых подшипников k=0,001 cм .

Отношение k/R для большинства материалов значительно меньше, чем коэффициент трения скольжения f . Поэтому в технике стараются трение скольжения заменить трением качения.

Статика. Равновесие тел под действием системы сходящихся сил

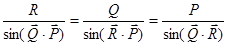Введение

Успешное освоение темы, связанной с изучением системы сходящихся сил, является основой для дальнейшего изучения статики. В теоретической части методических указаний изложены основные определения и теоремы для системы сходящихся сил, приведены примеры решения типовых задач для плоской и пространственной системы сходящихся сил. Индивидуальное задание 1 содержит варианты задач, в которых необходимо вычислить неизвестные реакции опор. В задании 2 требуется, используя теорему о трех силах, рассчитать неизвестные реакции опор и вычислить усилия в стержнях плоской фермы. В задании 3 необходимо определить усилия в стержнях пространственной фермы.

Система сил, приложенных в одной точке.

Основная задача статики заключается в определении условий, при которых тело находящееся под действием системы сил, сохраняет состояние покоя. Вспомогательная задача, которая возникает при решении основной, заключается в том, чтобы произвольную систему сил, действующую на тело, заменить равнозначной ей простейшей системой сил.

Рассмотрим основную и вспомогательную задачи статики для частного случая системы сил – системы сходящихся сил 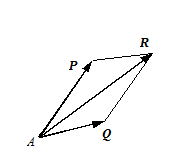. Пусть даны две силы 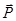и 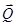, приложенные в одной точке А . Для системы двух сил, приложенных в одной точке, вспомогательная задача статики – приведение этой системы сил к простейшей системе – решается на основе четвертой аксиомы статики. Эти две силы можно заменить эквивалентной им одной силой (равнодействующей), которая равна их геометрической сумме 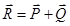. Модуль равнодействующей 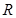определяется согласно теореме косинусов 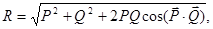где 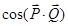косинус угла между направлениями сил 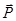и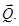

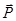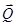Угол, который составляет вектор равнодействующей с векторами сил и определяется согласно теореме синусов

Решение обратной задачи – разложения данной силы 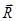на две эквивалентные ей силы 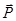и 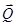- возможно в трех случаях: 1) заданы линии действия искомых сил, 2) задано направление и модуль одной силы, 3) заданы модули двух искомых сил. Для решения первой задачи на заданных направлениях сил строится параллелограмм, у которого диагональю является вектор силы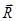

Во втором случае на направлении силы 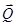откладывается отрезок, равный заданному модулю этой силы, затем строится параллелограмм, у которого диагональю является вектор силы 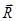. В третьем случае из концов вектора 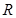проводятся две окружности, радиусы которых равны модулям заданных сил.

Точки пересечения окружностей используются для построения искомых сил. В третьем случае задача имеет два решения (одно решение строится по верхней точке пересечения окружностей, другое – по нижней).

Пусть задано 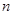сил 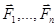, приложенных в одной точке. Применяя последовательно аксиому параллелограмма сил, получим, что равнодействующая системы сил, приложенных в одной точке существует, равна геометрической сумме всех сил и приложена в той же точке.

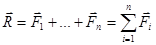Равнодействующая 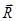может быть получена или графически или аналитически через проекции составляющих сил на оси координат. Для графического определения равнодействующей системы сил необходимо или последовательно применить нужное число раз правило параллелограмма или построить силовой многоугольник. При построении силового многоугольника начало каждой последующей силы откладывается от конца предыдущей. Равнодействующая имеет начало, совпадающее с началом первой силы и конец, совпадающий с концом последней силы.

В случае аналитического определения равнодействующей получим

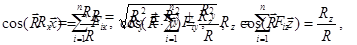Последние формулы, задающие модуль и направляющие косинусы равнодействующей рассматриваемой системы сил, вполне определяют ее.

Таким образом, мы получили решение вспомогательной задачи статики для системы n сил, приложенных в одной точке – эту систему можно заменить эквивалентной ей простейшей системой, состоящей из одной силы (равнодействующей исходной системы сил).

1. Равнодействующая системы сходящихся сил.

Определение.Система действующих на абсолютно твердое тело сил 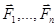, обладающая тем свойством, что линии действия всех сил системы пересекаются в одной точке О, называется системой сходящихся сил.

Нетрудно видеть, что случай системы сходящихся сил сводится к случаю системы сил, приложенных в одной точке. Действительно, согласно следствию из аксиомы 2 статики, мы можем все силы, не изменяя их действия на тело, перенести вдоль линий их действия в точку О и заменить данную систему эквивалентной ей системой сил, приложенных в точке О.

Следовательно, система сходящихся сил имеет равнодействующую, равную сумме этих сил и проходящую через точку, в которой пересекаются линии действия сил. Это означает, что для системы сходящихся сил вспомогательная задача статики решается так же, как и для системы сил, приложенных в одной точке.

Вычисление равнодействующей возможно либо с помощью построения силового многоугольника, либо аналитически с использованием формул (1)-(3).

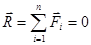Условия равновесия.Так как система сходящихся сил, имеет равнодействующую, то для равновесия этой системы сил необходимо и достаточно, чтобы равнодействующая системы 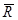была равна нулю,

Этот результат дает решение основной задачи для системы сходящихся сил: для равновесия тела, на которое действует система сходящихся сил, необходимо и достаточно, чтобы равнодействующая этой системы (которая всегда существует и равна геометрической сумме всех сил) была равна нулю.