Капиллярные явления. Пористые адсорбенты

Капиллярные явления связаны с искривлением поверхности раздела фаз.

Так, на жидких поверхностях поверхностное натяжение σ вызывает возникновение добавочного капиллярного давления ΔР, связанного с радиусом кривизны r соотношением

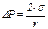(I)

в случае сферической поверхности раздела фаз;

и соотношением

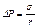(II)

в случае цилиндрической поверхности раздела фаз.

Вблизи твёрдой поверхности поверхность жидкости искривляется вследствие смачивания (вогнутый мениск) или несмачивания (выпуклый мениск) (рис.5). Как показано на рис. 5, капиллярное давление направлено в сторону центра кривизны. Ему противодействует гидростатическое давление, которое пропорционально высоте поднятия жидкости в капилляре h.

При равновесии оба давления равны друг другу, т.е.

ΔР = ρ·g·h (1)

или

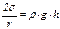(2)

Обычно радиус кривизны r заменяют известной величиной – радиусом капилляра r_o, используя соотношение

r_o = r·cos θ (3)

Совместное решение уравнений (2) и (3) приводит к следующему равенству:

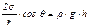(4)

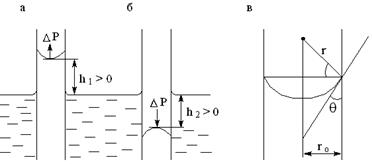
Рис. 5. Капиллярные явления:

а – жидкость смачивает стенки капилляра (отрицательная кривизна);

б – жидкость не смачивает стенки капилляра (положительная кривизна);

в – схематичное изображение мениска: r_o – радиус капилляра; θ – угол смачивания

Если принять, что поверхность раздела фаз имеет форму полусферы, то формула (4) упрощается:

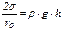(5)

Пористыми называют те твёрдые тела, внутри которых имеются поры, обусловливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью.

Для характеристики адсорбента используется понятие «пористость» П:

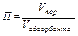(6)

По размеру пор и механизмам протекающих в них процессов пористые тела подразделяют на микропористые, мезопористые и макропористые.

Микропористые тела обладают порами, соизмеримыми с теми молекулами, адсорбция которых изучается. Радиусы таких пор лежат в пределах от 05, нм до 1,5-2 нм. К микропористым телам относятся цеолиты, активные угли и некоторые ксерогели.

Мезопористые тела характеризуются радиусами пор в пределах от 2 до 100-200 нм. К ним относятся активированные угли, силикагели, алюмогели и другие адсорбенты.

Макропористые тела имеют поры радиусом больше 100-200 нм. Такие поры по сравнению с адсорбированными молекулами – выглядят как ровные поверхности, поэтому к ним применимы теории адсорбции на гладкой поверхности.

Теория Поляни называется потенциальной теорией объёмного заполнения микропор. В основе этой теории лежит представление о силовом (потенциальном) поле адсорбента, распространяющемся на значительное расстояние от поверхности.

Размеры микропор таковы, что в них происходит перекрытие полей поверхностных сил противоположных стенок пор. В это поле, напоминающее атмосферу, «попадают молекулы» газа, в порах происходит уплотнение молекул. В теории Поляни сделано допущение о том, что практически все вещества в порах находятся в жидком состоянии.

В качестве меры интенсивности взаимодействия между микропористым телом и газом принят адсорбционный потенциал ε, который численно равен работе переноса 1 моль вещества с поверхностного слоя с давлением насыщенного пара Р_о в равновесную газовую фазу с давлением Р:

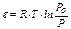(7)

При заполнении пор жидким адсорбатом граница между жидкостью и газовой фазой искривляется – возникает капиллярное давление.

При равновесии работа гравитационных сил уравновешивается работой капиллярных сил А_к в расчёте на 1 моль жидкости:

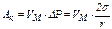, (8)

где r – радиус кривизны, который в данном случае из-за малого размера пор совпадает с их радиусом; σ – поверхностное натяжение жидкости; V_M (м³/моль, см³/моль) – молярный объём жидкого адсорбата, равный отношению молярной массы к плотности этого адсорбата.

Приравнивая соотношение ε и А_к , получаем

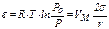. (9)

Используя уравнение (9), можно рассчитать радиус пор.

Задача теории – перейти от обычных координат изотермы к зависимости адсорбционного потенциала от расстояния от поверхности. Однако последнее для пористого адсорбента определить не представляется возможным, поэтому на практике расстояние от поверхности заменяется объёмом жидкого адсорбата φ, приходящегося на единицу массы адсорбента. Этот объём можно определить на основании экспериментальных данных, если известна величина удельной адсорбции Х (моль/г или моль/кг), по формуле

φ = Х·V_М . (10)

Кривая зависимости ε от φ называется характеристической кривой.

Обнаружено, что характеристические кривые, построенные по экспериментальным данным изотерм, инвариантны по отношению к температуре: всё семейство изотерм ложится на одну кривую ε – φ.

Второе важное свойство характеристических кривых таково: для одного и того же адсорбента и разных адсорбатов при всех значениях объёмов адсорбата в поверхностном слое все кривые находятся в постоянном отношении β:

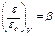, (11)

где ε_о – адсорбционный потенциал для адсорбата, выбранного в качестве стандартного.

Коэффициент β был назван коэффициентом аффинности (сродства).