Реальные цепи. Эффект исключенного объема
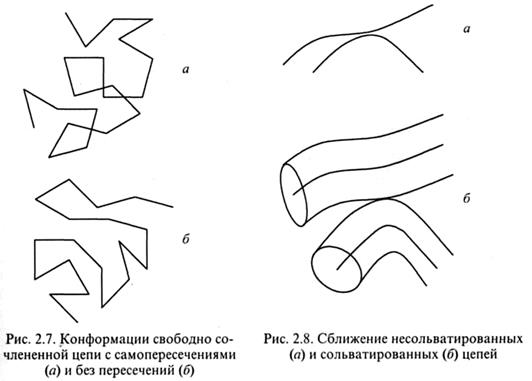
Реальные цепи отличаются от идеальных взаимодействием звеньев между собой и с молекулами растворителя. Эти взаимодействия могут быть как физическими, так и химическими, простейшими из них являются столкновения звеньев. Последний вид взаимодействия, несмотря на кажущуюся простоту, приводит к существенным отклонениям свойств клубка от идеального. Во-первых, это связано с тем, что реальные цепи в отличие от гипотетической, бестелесной свободно сочлененной цепи обладают собственным объемом. Поэтому взаимодействия, связанные со столкновениями звеньев, называются объемными. Они определяются так же, как эффект исключенного объема, т.к. при столкновении звеньев объем одного из них исключается как место возможного расположения другого. В результате конформационный набор реальных цепей по сравнению с идеальными заметно сужается из-за невозможности самопересечений и складывания отрезков цепи. Исключение соответствующих конформаций приводит к увеличению среднеквадратичного размера клубка. Выше говорилось о том, что свернутая конформация свободно сочлененной цепи соответствует траектории частицы при броуновском движении. На рис. 2.7 приведена эта траектория, наряду с траекторией (конформацией), реализуемой при запрете на самопересечение.
Второе обстоятельство, определяющее влияние объемных взаимодействий на размер клубка, связано с характером столкновений звеньев. Результат этих столкновений зависит от соотношения между кинетической энергией теплового движения звеньев и энергией когезии (притяжения). При «повышенных» температурах первая преобладает, столкновение звеньев приводит к их отталкиванию, т.е. носит упругий характер, в результате клубок увеличивается, разбухает по сравнению с идеальным. При «пониженных» температурах величина кинетической энергии недостаточна для того, чтобы преодолеть силы сцепления звеньев. В результате столкновение звеньев приводит к их притяжению, слипанию. Клубок в этом случае сжимается по сравнению с идеальным, возникает тенденция к агрегации клубков и выделению полимерной фазы (выпадение полимера в осадок). Продолжая рассуждения, мы приходим к логическому выводу о том, что существует промежуточная температура, при которой тенденции к разбуханию и сжатию клубка уравновешены, и он ведет себя как невозмущенный, т.е. идеальный. Подобное состояние макромолекул реализуется при определенной температуре и в определенных растворителях. Такая температура называется θ-температурой, а растворители - θ-растворителями. Представления о θ-условиях, в которых макромолекулярные клубки по размерам и другим свойствам аналогичны идеальным, так называемым невозмущенным или гауссовым, впервые введены Флори.
Особую группу представляют системы, в которых растворитель сольватирует цепи. Сольватные оболочки препятствуют сближению звеньев (рис. 2.8) и, тем самым, увеличивают исключенный объем и среднеквадратичный размер клубка.
При экзотермическом растворении, когда энергия межмолекулярного взаимодействия молекул растворителя со звеньями макромолекул велика, клубки являются разбухшими по сравнению с идеальными при любых температурах; в этих системах отсутствуют θ-условия и фазовое разделение. Количественно эффект разбухания клубка характеризуется коэффициентом набухания:

где 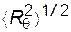 - среднеквадратичное расстояние между концами цепи в θ-условиях. При преобладании отталкивания звеньев α > 1, притяжения - α < 1, в идеальном растворителе (θ -условиях) α = 1.
- среднеквадратичное расстояние между концами цепи в θ-условиях. При преобладании отталкивания звеньев α > 1, притяжения - α < 1, в идеальном растворителе (θ -условиях) α = 1.
Экспериментально коэффициент набухания клубка наиболее просто может быть определен путем вискозиметрических измерений. Соответствующие соотношения будут рассмотрены далее. Величина а оказывает влияние на характер зависимости размера цепи от молекулярной массы. Возможные случаи отражены ниже:

Из приведенных зависимостей следует, что в растворах полимеров в хороших растворителях, для которых характерно условие α > 1, правило «квадратного корня» не выполняется, размер клубков связан с молекулярной массой цепи в степени, большей 0,5. Этот вывод подтвержден экспериментально. Так, для растворов полиметилметакрилата в ацетоне и поли-2,5-дихлорстирола в диоксане получено 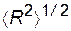 ~ M0,58, что достаточно близко к ожидаемому результату, исходя из (2.19).
~ M0,58, что достаточно близко к ожидаемому результату, исходя из (2.19).
В хороших растворителях имеет место слабая зависимость коэффициента набухания от молекулярной массы макромолекулы:

В плохих растворителях эту зависимость проследить не удается, так как при α < 1 растворы полимеров термодинамически неустойчивы.
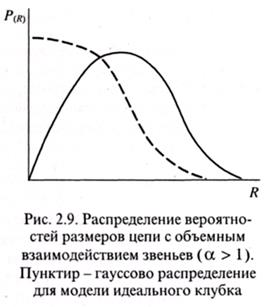
Набухание клубков в хорошем растворителе приводит к существенному изменению вида зависимости P(R) - R по сравнению с той, что была получена на основе модели идеальной цепи. Из рис. 2.9 следует, что в отличие от свободно сочлененной цепи для реальной вероятность сближения концов макромолекулы близка к нулю.
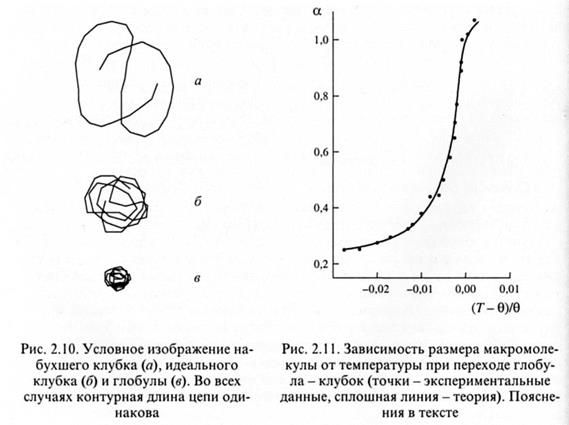
Из предыдущего следует, что значение а определяется природой растворителя и температуры. Следовательно, макромолекула в одном и том же растворителе в зависимости от температуры может иметь конформации трех типов, условное изображение которых приведено на рис. 2.10: набухшего клубка, идеального (гауссового) клубка и сжатого клубка, называемого глобулой (α < 1), для которых характерны существенно отличные зависимости размера от молекулярной массы. Поэтому можно ожидать, что изменение температуры в интервале, достаточном для изменения конформации клубка, оказывает сильное влияние на его размер. Изменение размера отдельных макромолекул можно наблюдать методами упругого и неупругого рассеяния света и нейтронов, поляризованной люминесценции, вискозиметрии, осмометрии и некоторыми другими. Во всех случаях необходимо использовать растворы полимеров очень малой концентрации. Это объясняется тем, что при Т < θ, как отмечалось выше, раствор полимера агрегативно неустойчив, и легко может выделиться в осадок. Для того, чтобы этого не произошло, необходимо работать с очень разбавленными растворами полимеров. Одной из крайне ограниченного числа систем, изученных в этих условиях, является система полистирол-циклогексан, θ-температура для которой равна 35 °С. Из рис. 2.11 видно, что в интервале температур, равном всего лишь нескольким градусам, коэффициент а уменьшается в несколько раз, что отвечает уменьшению объема клубка на порядок. Конформационный переход при T ≈ 0, сопровождающийся резким изменением объема клубка, называется переходом клубок-глобула. Этот переход выражен тем в большей степени, чем более жесткой является цепь.
Уравнение состояния набухшего клубка. Рассмотренное выше явление разбухания клубка (α > 1) в хорошем растворителе может быть наглядно интерпретировано, если рассматривать макромолекулярный клубок как миниатюрную осмотическую ячейку. Известно, что осмотический эффект заключается в диффузии растворителя через мембрану в ячейку и возникновении вследствие этого осмотического давления. В случае макромолекулярного клубка осмотический эффект будет приводить к увеличению размера, т.е. разбуханию клубка. Деформация клубка, вызванная его набуханием, приводит к возникновению силы упругости, которая препятствует его дальнейшему набуханию. В результате устанавливается некое равновесное состояние клубка, которому соответствует равновесное значение коэффициента набухания. Выражение для равновесного коэффициента набухания клубка впервые получено Флори. В упрощенной форме оно может быть представлено следующим образом:

где z - параметр, характеризующий исключенный объем раствора полимера. В простейших случаях величина исключенного объема может быть легко рассчитана. Рассмотрим, например, заполнение раствора макромолекулами радиуса R, моделирующими глобулярные белки. Ясно, что центры массы плотных шарообразных молекул могут сближаться на расстояние 2R. Отсюда:

где Vискл - исключенный объем; М2 - молекулярная масса растворенного вещества; V2 - удельный объем частиц растворенного вещества; NA - число Авогадро. Аналогичный подход по отношению к раствору плотных стержней приводит к

где L - длина; d - диаметр стержня.
Задача расчета исключенного объема в случае гибкоцепных полимеров является более сложной, она будет рассмотрена в разд. 3.1.6, наряду с
содержанием параметра z. Здесь же необходимо обратить внимание на то, что параметр z включает множитель (1 - θ/T). Отсюда:

Концентрационные эффекты. Все рассмотренное выше относится к разбавленным растворам полимеров, в которых макромолекулярные клубки не перекрываются. Ясно, что такая ситуация будет сохраняться до тех пор, пока средняя плотность звеньев в клубке не превысит плотность собственных звеньев в нем. Последняя величина определяется формулой (2.16), следовательно, исходя из нее, можно вычислить некую критическую концентрацию φ2кр (φ2 - объемная доля полимера в растворе), выше которой клубки начинают перекрываться. Расчеты показывают, что в растворах полимеров с молекулярной массой 105 - 106 φ2кр не превышает 0,01 (1 %) для идеальных растворов полимеров с молекулярной массой порядка 105. Растворы полимеров называются разбавленными при условии φ2 < φ2кр и полуразбавленными при φ2 > φ2кр.
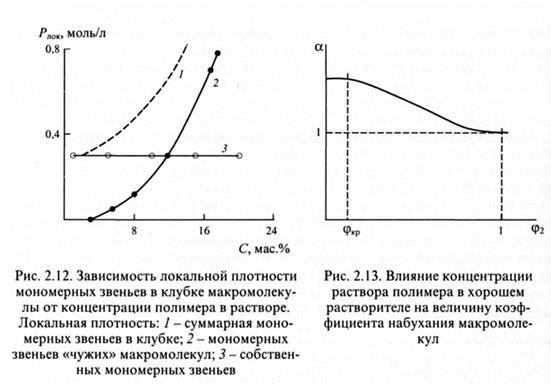
Каким образом отразится увеличение концентрации раствора на объемных взаимодействиях? На этот вопрос можно ответить вполне определенно, исходя из чисто умозрительных рассуждений. Объемные взаимодействия есть результат притяжения или отталкивания звеньев одной цепи. С увеличением концентрации раствора в клубок все больше проникает звеньев другой цепи, что иллюстрируется рис. 2.12. Следовательно, контакты звеньев одного клубка все в большей степени заменяются на контакты звеньев разных клубков. Это должно привести к прогрессивному уменьшению эффектов объемного взаимодействия, в частности уменьшению исключенного объема и уменьшению а. В расплаве любое звено цепи окружено «чужими». Поэтому можно утверждать, что в расплаве роль объемных взаимодействий сведена на нет. Впервые подобные рассуждения высказал Флори; на основании их он заключил, что в расплаве реализуются θ-условия, и клубок является идеальным. Это утверждение называется теоремой Флори. Расплавы аморфных полимеров при охлаждении стеклуются, в результате конформации идеальных клубков фиксируются, «замораживаются». Следовательно, θ-состояние, т.е. состояние идеального клубка, характерно не только для разбавленных растворов и расплавов, но и для стекол полимеров. Этот вывод подтверждают, в частности, значения среднеквадратичных радиусов инерции макромолекул полистирола различной молекулярной массы в блоке и в разбавленных растворах в θ-растворителе циклогексане; радиусы инерции измерены методом рассеяния нейтронов:
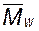 ·10-3 ·10-3 | 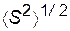 , нм (раствор) , нм (раствор) | 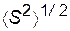 , нм (блок) , нм (блок) |
| 3,8 10,7 29,7 | 4,2 11,7 29,3 |
Аналогично в случае полиметилметакрилата было найдено, что в растворе н-бутилхлорида (θ-растворитель) 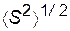 = 12,5 нм, тогда как в блоке
= 12,5 нм, тогда как в блоке 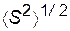 =
=
= 11,0 нм.
Теоретические расчеты, а также прямой эксперимент подтверждают теорему Флори. На рис. 2.13 приведена качественная зависимость α от концентрации раствора полимера в хорошем растворителе. Из этого рисунка следует, что с увеличением концентрации раствора величина α и, следовательно, значение объемных эффектов уменьшается. При φ2 = 1, что соответствует состоянию расплава или полимерного стекла, α = 1, т.е. макромолекулярные клубки являются идеальными, гауссовыми.
Гибкость цепи
Различают два вида гибкости цепи: термодинамическую (статистическую) и кинетическую (динамическую). Первая является равновесной, она определяется химическим строением макромолекул и реализуется в результате теплового движения отрезков цепи. Макромолекулы в растворах участвуют в тепловом движении посредством макроброуновского и микроброуновского движения. В первом случае макромолекулы перемещаются как целое, во втором - перемещаются отдельные кинетически независимые отрезки цепи, называемые сегментами. Микроброуновское движение осуществляется за счет столкновений сегментов макромолекул с другими сегментами или молекулами растворителя. В каждый момент времени сегмент претерпевает множество столкновений. Как правило, результирующий момент силы не равен нулю, в результате сегмент движется в направлении результирующего момента, а вместе с ним в эту сторону выгибается макромолекула. Многократные изгибы макромолекулы, являющиеся следствием ее участия в тепловом молекулярно-кинетическом движении, приводят к свертыванию макромолекулы в клубок. Кинетическая гибкость характеризует скорость конформационных переходов, т.е. время, необходимое для смены локальных конформаций. Существует два механизма термодинамической гибкости, один из которых применим для гибкоцепных полимеров, другой - для жесткоцепных.
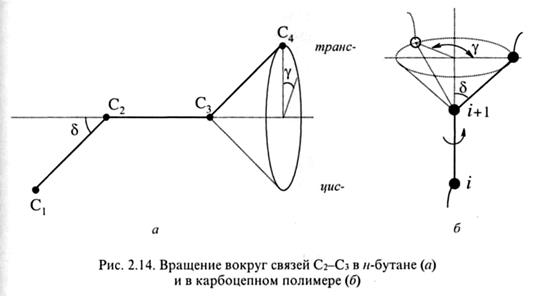
Поворотно-изомерный механизм гибкости цепи. К гибкоцепным полимерам относятся полиолефины, большинство полимеров виниловых и винил-диеновых мономеров общей формулы -(СН2-СНХ)-, -(CH2-CXY)-, где X, Y -заместители основной цепи. Гибкость таких полимеров обусловлена свободой вращения вокруг простых связей основной цепи, механизм гибкости называется поворотно-изомерным. Рассмотрим детали этого механизма на примере н-бутана, который можно представить как фрагмент цепи полиэтилена (рис. 2.14). При вращении связи C1-С2 или С3-С4 описывается конус с образующей, направленной под углом δ к оси вращения. Угол δ является дополнительным к валентному, т.е. δ = π - 190°. При вращении связи С3-С4 атом С4 описывает окружность, в плоскости которой лежит угол вращения ץ, отсчитываемый относительно транс-положения. Расстояние между конечными атомами C1 и С4 при вращении изменяется и составляет, как показывает расчет, 0,2 нм для цис- и 0,38 для транс-формы. Поскольку радиусы Ван-дер-Ваальса метильной группы примерно равны 0,2 нм, можно ожидать стерического напряжения цис-формы. В этом случае вращение вокруг связи С2-С3 не будет свободным. Вследствие взаимного отталкивания заместителей в i/wc-положении возникают потенциальные барьеры вращения.
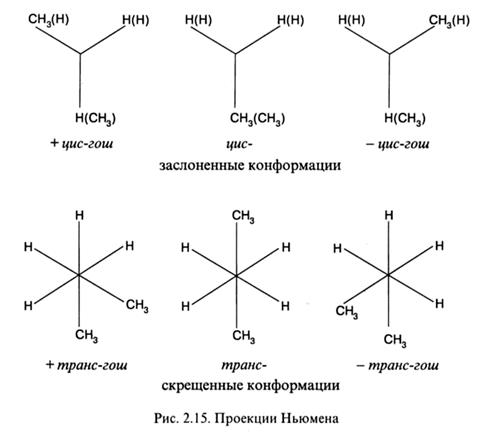
Наличие заторможенного вращения вокруг связей С-С нормальных парафинов впервые было экспериментально обнаружено М.С.Ньюменом. По методу Ньюмена изменение формы молекул в результате вращения связей изображают проекциями связей на плоскость, нормальную к оси вращения (рис. 2.15).
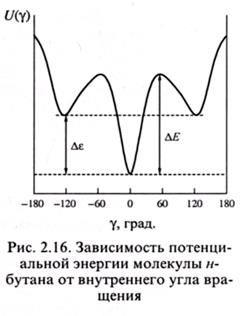
Если смотреть вдоль оси С3-С2, то при вращении связи С3-С4 возможны заслоненные конформации, когда проекции связей на плоскость совпадают (цис- и цис-гош), и заторможенные (скрещенные) конформации (транс- и транс-гош) (на рис. 2.15 заслоненные конформации обозначены скобками). При вращении вокруг связи С2-С3 потенциальная энергия системы периодически изменяется – транс-конформациям отвечают минимумы энергии, цис-конформациям - максимумы (рис. 2.16). Наиболее глубокий минимум отвечает транс-конформации, от которой отсчитывается угол ץ. При вращении по часовой стрелке гош-конформациям приписывается знак «+», при вращении против часовой стрелки - знак «-». Аналогично обозначение конформации, возникающих при вращении вокруг связей С-С основной цепи полимеров виниловых мономеров (см. рис. 2.14, б).
Разница между максимальной энергией, отвечающей заслоненной цис-конформации, и минимальной энергией, отвечающей скрещенной транс-конформации в н-бутане, настолько значительна, что свободного полного вращения вокруг связи С2-С3 не происходит. Молекула находится в одной из
конформаций с минимальными значениями энергии: транс-, -транс-гош и +транс-гош формах. Энергии этих конформаций отличаются всего на 2,5 кДж/моль (Δε), а потенциальные барьеры (ΔЕ), разделяющие их, равны 14 кДж/моль, т.е. также относительно невелики, поэтому происходит постоянная смена конформаций в результате частичного неполного заторможенного вращения вокруг связи С2-С3. Потенциальные барьеры заторможенного вращения получили название потенциалов торможения. Представления о конформационной изомерии молекул алканов распространены на макромолекулы М.В.Волькенштейном, который впервые предложил поворотно-изомерную модель полимерной цепи. Согласно этой модели, заторможенное вращение
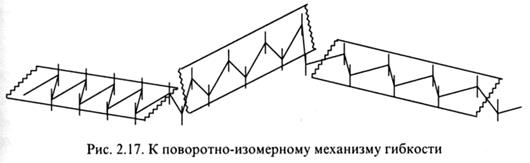
вокруг связей основной цепи осуществляется дискретно, в результате чего фиксируются конформаций транс-, +транс-гош, -транс-гош. Конформацией с наименьшей энергией является плоский зигзаг основной цепи, отвечающий транс-конформации, и ץ = 0. Вращение вокруг любой из ее σ-связей приводит к излому плоской ленты в том месте, где ץ ≠ 0. Совокупность изломов вызывает свертывание цепи в клубок (рис. 2.17).
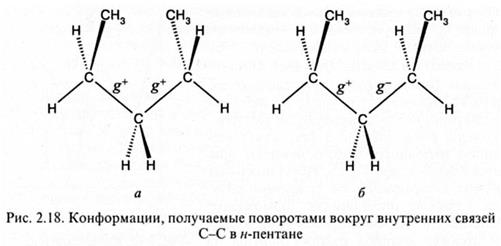
В случае макромолекул потенциальные барьеры внутреннего вращения связей становятся зависящими от состояния (углов вращения) соседних связей. Наиболее значимым эффектом является запрет на гош-повороты противоположного знака в соседних связях (так называемый «пентановый эффект»). На рис. 2.18 приведены конформаций, получаемые поворотами вокруг внутренних связей С-С в н-пентане. Из рис. 2.18, б видно, что при g+g- поворотах конечные группы СН3 находятся по одну сторону плоскости, в которой лежат две внутренние С-С-связи, и на достаточно близком расстоянии друг от друга. Пространственные модели показывают, что это расстояние равно 0,25 нм. Выше упоминалось, что радиус Ван-дер-Ваальса метильной группы равен 0,2 нм. Из этого следует, что при сближении метильных групп стерическое отталкивание должно возникать на расстояниях, меньших 0,4 нм, и для g+g- конформации н-пентана оно должно быть весьма значительно.
В случае стереорегулярных изотактических полимеров энергетически наиболее выгодной конформацией является спираль, для которой в наименьшей степени проявляется отталкивание заместителей в изо-триадах звеньев. Так, в макромолекуле изотактического полипропилена каждое звено повернуто относительно другого на 120°, т.е. в триаде последовательно представлены +транс-гош, транс- и -транс-гош конформеры. После упаковки в кристалл спиральные конформации цепей не изменяются, однако, в растворе или расплаве спирали также свертываются в клубки в результате изменения углов вращения вокруг связей основной цепи.
Как термодинамическая, так и кинетическая гибкость зависят от соотношения величин Δε и ΔЕ с тепловой энергией. Если Δε < kТ, то цепь является термодинамически гибкой. В этом случае, как показано выше, в отдельных местах плоского зигзага основной цепи возникают изломы, и в целом она выглядит как рыхлый клубок. При Δε << kТ цепь является предельно гибкой, она сворачивается в более плотные клубки по сравнению с предыдущим случаем. В качестве примера можно указать на полиметилсилоксановый каучук, макромолекулы которого сворачиваются в плотные клубки.
Применительно к изложенному механизму гибкости, «формула квадратного корня» трансформируется в следующие выражения:
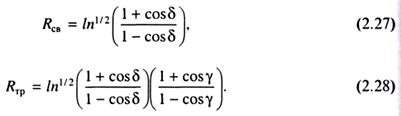
Первое из них относится к цепи со свободным вращением вокруг связей (Δε << kТ), здесь δ - угол, дополнительный к валентному. Второе относится к цепям с ограниченным вращением вокруг связей - на угол ץ. В обоих выражениях l - длина, n - число звеньев. Существуют зависимости, связывающие углы вращения вокруг связей основной цепи с потенциалами торможения. В некоторых достаточно простых случаях потенциалы торможения удается рассчитать. Тогда выражение (2.28) может быть использовано непосредственно для расчета размера макромолекул. Однако более часто выражения (2.27) и (2.28) используются для оценки гибкости цепи. Отношение

является мерой гибкости цепи. Величина Rсв может быть легко рассчитана, т. к. величины валентных углов известны. Величина Rтр определяется экспериментально. В последнем случае необходимо использовать идеальный, так называемый θ-растворитель, который не оказывает возмущающего влияния на размеры клубков. С учетом этого

где σ - стерический фактор или фактор гибкости.
Термодинамический сегмент Куна. Модель идеальной свободно сочлененной цепи в определенных условиях может быть применена к реальным макромолекулам. Хотя в последних полная свобода вращения вокруг одной связи в большинстве случаев отсутствует, последовательность нескольких связей обеспечивает полную свободу ориентации, т.е. кинетическую независимость связываемых ими отрезков цепи. В качестве примера можно указать на цепь из канцелярских скрепок. Две скрепки можно повернуть относительно одна другой на угол, примерно равный 180°, однако последовательность нескольких скрепок обеспечивает полную свободу вращения и независимость ориентации связываемых ими отрезков цепи. Из сказанного следует, что любую реальную цепь гибкоцепного полимера условно можно представить в виде последовательности кинетически независимых отрезков цепи -сегментов. Очевидно, что, чем гибче цепь, тем меньше длина сегмента и наоборот. Следовательно, длина сегмента характеризует термодинамическую гибкость цепи. Поэтому он называется термодинамическим или сегментом Куна - по имени ученого, впервые предложившего изложенный подход.
Длина термодинамического сегмента Куна l* или связанная с ней величина числа звеньев в сегменте n* определяется, исходя из двух простых соотношений:

где L - контурная длина; 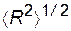 - расстояние между концами; n - число звеньев в макромолекуле. Величина
- расстояние между концами; n - число звеньев в макромолекуле. Величина 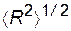 , как уже говорилось, определяется методами вискозиметрии, седиментации и светорассеяния. Контурная длина цепи для полимеров виниловых мономеров определяется, исходя из простого соотношения:
, как уже говорилось, определяется методами вискозиметрии, седиментации и светорассеяния. Контурная длина цепи для полимеров виниловых мономеров определяется, исходя из простого соотношения:

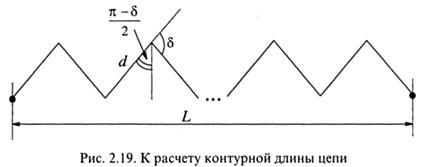
где δ - угол, дополнительный к валентному; d - длина связи С-С; n - число мономерных звеньев в цепи. Смысл формулы становится понятным из рассмотрения рис. 2.19.
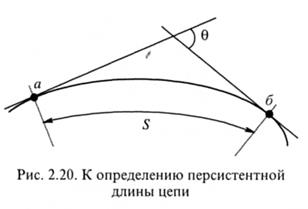
Персистентная гибкость. Другой механизм реализуется в случае цепей равномерной гибкости жесткоцепных полимеров. К ним относятся макромолекулы двухтяжевых полимеров, в частности, двойная спираль ДНК. Общей причиной равномерной гибкости является незначительная, в пределах нескольких градусов, деформация валентных углов, а также малые (до 3 %) колебания длин связей. Эта гибкость невелика, тем не менее, благодаря ей достаточно удаленные отрезки цепи могут ориентироваться независимо. В качестве примера рассмотрим стальную проволоку. Короткий отрезок проволоки не только не имеет изломов, но и его кривизна незначительна, практически не заметна на глаз. Тем не менее длинный отрезок проволоки самопроизвольно принимает форму неупорядоченной спирали. Изложенный механизм гибкости называется персистентным. Количественной характеристикой персистентной гибкости является так называемая персистентная длина 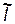 , определяемая соотношением (2.34), которое, в свою очередь, иллюстрируется рис. 2.20. Здесь S - контурная длина отрезка цепи постоянной гибкости, θ - угол между касательными, проведенными к концам отрезка, характеризующий его изгибание, cosθ - средний косинус угла изгибания (закручивания в случае цепи):
, определяемая соотношением (2.34), которое, в свою очередь, иллюстрируется рис. 2.20. Здесь S - контурная длина отрезка цепи постоянной гибкости, θ - угол между касательными, проведенными к концам отрезка, характеризующий его изгибание, cosθ - средний косинус угла изгибания (закручивания в случае цепи):

Анализ формулы (2.34) приводит к следующим выводам. При  >> S cosθ → 1, это означает, что данный отрезок близок к форме стержня. При
>> S cosθ → 1, это означает, что данный отрезок близок к форме стержня. При  << S cosθ → 0 , что соответствует неупорядоченному искривлению S и потере корреляции между концами. В данном случае cosθ может принимать
<< S cosθ → 0 , что соответствует неупорядоченному искривлению S и потере корреляции между концами. В данном случае cosθ может принимать
любые значения - положительные и отрицательные. Поскольку ни одна из конформаций не имеет преимуществ, то среднее значение cosθ равно нулю. Строго доказано, что длина термодинамического сегмента Куна связана с персистентной длиной соотношением:

В табл. 2.2 приведены значения стерического фактора и длины сегмента Куна, характеризующие термодинамическую гибкость цепи для некоторых классов полимеров и отдельных представителей. Напомним, что увеличение значений обоих параметров свидетельствует об ухудшении гибкости цепи. Из табл. 2.2 следует, что наибольшей гибкостью обладают гетероцепи, содержащие атомы серы и кислорода. Ясно, что причина аномально большой гибкости таких цепей связана со свободой вращения вокруг связей атомов, не имеющих заместителей. Причина достаточно большой гибкости цепей полимеров диенов связана с большей, по сравнению с полимерами виниловых мономеров, свободой вращения вокруг связей, примыкающих к двойным.
К снижению гибкости цепи приводит наличие в ней циклов и сопряжение атомов, входящих в состав основной цепи. Первое можно видеть на примере целлюлозы и ее производных, а также поли-n-бензамидов. Значения параметров гибкости обоих классов намного превышают те, что характерны для

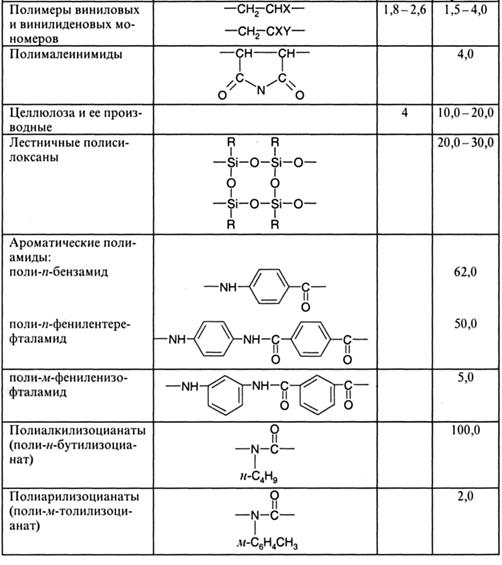
полимеров виниловых мономеров. Однако само по себе наличие циклов в цепи не всегда приводит к существенному ужесточению цепи. Этому может помешать наличие гибких мостиков между циклами или отсутствие сопряжения между ними. Так, из табл. 2.2 видно, что поли-n-фенилентерефталамид имеет существенно более жесткую цепь по сравнению с соответствующим мета-полимером. Это объясняется большей энергией сопряжения в цепи в первом случае, из-за чего вращение вокруг связей цепи, нарушающее это сопряжение, является энергетически невыгодным. Еще более ярко эффекты сопряжения проявляются в поли-алкил(арил)-изоцианатах. Это обусловлено затрудненностью вращения вокруг связи C-N в амидной группе, что хорошо видно из мезомерной структуры, указывающей на увеличение двоесвязанности этой связи в результате p-π-сопряжения (напомним, что вращение вокруг кратных связей невозможно):

Поли-н-бутилизоцианат имеет одну из наиболее жестких цепей, поскольку последняя образована амидными связями, сопряженными между собой. В случае р-π-сопряжения этот эффект наиболее наглядно может быть выражен мезомерными, т.е. резонансными структурами:

где R - н-С4Н9. Наличие сопряжения и двоесвязанности между атомами цепи препятствует вращению вокруг любой ее связи.
Иная ситуация характерна для поли-м-толилизоцианата:
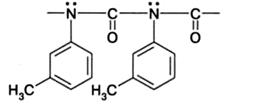
Сопряжение в основной цепи этого полимера отсутствует, поскольку энергетически более выгодным оказывается р-π-сопряжение неподеленной пары азота с ароматическим заместителем. Поэтому вращение вокруг связей основной цепи достаточно свободно, так как оно не изменяет столь существенно внутренней энергии системы, как в предыдущем случае, и цепь является существенно менее жесткой.
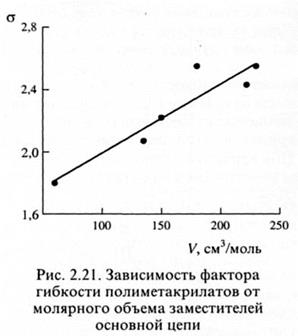
Заместители оказывают меньшее влияние на гибкость основной цепи по сравнению с ее строением и химическим составом. Из рис. 2.21 видно, что увеличение молярного объема заместителя приводит к закономерному возрастанию жесткости цепи в ряду полиметакрилатов. При переходе от полиметил- (I) к полицетил- (II) и полиоктил- (III) акрилатам длина сегмента Куна возрастает от 2 до 5-6 нм, при этом объем заместителя возрастает на порядок.
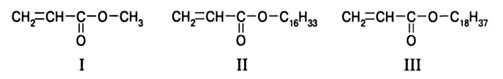
При сравнении полимеров разнотипных мономеров значение этого фактора проявляется менее определенно, но все же упомянутая выше тенденция прослеживается (табл. 2.3). Более существенно на гибкость цепи влияет полярность заместителя, о чем можно судить, сравнив параметры гибкости
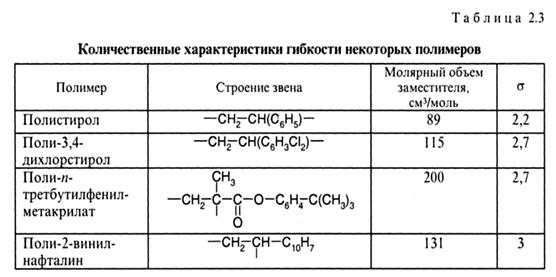
полипропилена и полиакрилонитрила. Оба полимера имеют близкие объемы заместителя, но полярность заместителя выше у полиакрилонитрила. Группа -C≡N является одной из наиболее полярных, ее дипольный момент близок к 4 D.
Гибкость цепи оказывает влияние на многие свойства полимера, в частности, на температуру стеклования (см. разд. 4.2.2).
Кинетическая гибкость цепи. Кинетическая гибкость цепи определяется, в первую очередь, величиной потенциальных барьеров вращения, а также внутри- и межмолекулярным взаимодействием. Последнее особенно существенно для конденсированного состояния полимеров. Потенциальные барьеры вращения простых молекул определяются спектральными методами по температурной зависимости интенсивности поглощения.
В табл. 2.4 приведены потенциальные барьеры вращения для некоторых соединений. В случае n-бутана приведенное значение относится ко второму, меньшему максимуму (см. рис. 2.16). Из таблицы следует, что наиболее низки потенциальные барьеры вращения вокруг связей С-О, C-S, C-Si, C-C=C. Известно, что еще более низкими являются потенциальные барьеры вращения вокруг связей Si-O, P-O, P-N. Полимеры, содержащие в основной цепи упомянутые связи, имеют большую кинетическую гибкость. Для реализации кинетической гибкости необходимо, чтобы величина потенциального барьера вращения была соизмерима с кинетической энергией теплового движения сегментов. Кинетическая или динамическая гибкость цепи зависит от высоты потенциального барьера ΔE, разделяющего транс- и транс-гош состояния.
Таблица 2.4 Высоты барьеров для типичных потенциалов внутреннего вращения
| Соединение и связь | Высота барьера, кДж/моль | Соединение и связь | Высота барьера, кДж/моль |
| CH3-CH3 | 11,7 | CH3-SH | 4,45 |
| CH3-CH(CH3)2 | 16,4 | CH3-NH2 | 8,0 |
| CH3-C(CH3)3 | 18,5 | CH3-SH3 | 7,1 |
| CH3-CH=CH2 | 8,2 | CF3-CF3 | 18,3 |
| CH3CH2-CH2CH3 | 14,6 | CH3-CH=O | 4,9 |
| CH3-CF3 | 15,5 | CH3-OCH3 | 11,4 |
| CH3-OH | 4,5 | CH3-PH2 | 8,2 |
Если ΔE ≈ kТ, то переход между двумя локальными конформациями или транс-гош-изомеризация может происходить за время 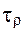 порядка 10-11 с, что отвечает кинетической гибкости цепи. В общем случае:
порядка 10-11 с, что отвечает кинетической гибкости цепи. В общем случае:

где 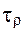 - время, необходимое для изменения локальной конформации;
- время, необходимое для изменения локальной конформации; 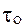 - величина, близкая 10-14 с.
- величина, близкая 10-14 с.
Макромолекулы могут обладать значительной термодинамической и малой кинетической гибкостью, например макромолекулы с гибкой основной цепью и объемными или полярными заместителями. В этом случае клубок «заторможен» в одном из конформационных состояний. Кинетическая гибкость, т.е. скорость изменения конформации может быть увеличена в результате воздействия на макромолекулу внешних сил.
Помимо химического состава и строения основной цепи и заместителей, кинетическая гибкость зависит от следующих факторов:
а) межцепного физического взаимодействия - в полимерных телах кинетическая гибкость всегда меньше по сравнению с растворами;
б) сшивки макромолекул - с увеличением плотности сшивки кинетическая гибкость падает;
в) молекулярной массы полимера - макромолекулы большей длины имеют более высокую гибкость по сравнению с менее длинными.
Кинетическая гибкость может проявляться как в растворе, так и в конденсированных полимерных телах. В первом случае она проявляется наиболее ярко в гидродинамическом поле. При действии больших напряжений сдвига макромолекулы разворачиваются. Кинетическая гибкость макромолекул в растворе характеризуется величиной кинетического сегмента, т.е. минимальным отрезком цепи, который может изменять форму под действием внешней силы. Длина кинетического сегмента зависит от скорости воздействия, с ее уменьшением длина кинетического сегмента уменьшается и стремится к длине термодинамического сегмента.
В конденсированном состоянии полимеров кинетическая гибкость цепи начинает проявляться при температурах, превышающих температуру стеклования. Кинетическую гибкость макромолекул в полимерных телах характеризуют длиной механического сегмента, равной длине цепи, при которой исчезает зависимость температуры стеклования полимера от молекулярной массы.
Гибкость цепи оказывает большое влияние на свойства полимеров и определяет области их использования. Например, кинетическая гибкость приводит к возникновению у полимеров такого уникального и технически важного свойства, как высокоэластичность, кроме того, она обусловливает способность макромолекул к ориентации, что имеет огромное значение при формировании волокон. Термодинамическая гибкость проявляется в процессах кристаллизации, плавления и растворения полимеров.
