Стандартизация по перманганату калия

Проводится методом обратного перманганатометрического титрования с йодометрическим окончанием. К точно известному объему стандартного раствора перманганата калия, взятого в избытке по сравнению со стехеомет-рическим количеством, прибавляют серную кислоту, нагревают. После этого добавляют точно измеренный объем стандартного раствора нитрита натрия и оставляют смесь на 15-20 минут. При этом протекает реакция:

5NO₂^- +2MnO₄^- + 6H⁺→5NO₃^-+ 2Mn²⁺ + 3H₂O

Затем к раствору добавляют избыток 10% раствора иодида калия. Иодид калия взаимодействует с непрореагировавшим перманганатом калия с образованием йода:

2MnO₄^- +10 I^- +16 H⁺→2Mn²⁺ +5 I₂ + 8H₂O

Образовавшуюся смесь разбавляют водой и оттитровывают выделившийся йод стандартным 0,05 моль/л раствором тиосульфата натрия до слабо желтой окраски раствора. Добавляют 1-2% раствор крахмала, раствор окрашивается в синий цвет. Продолжают титрование до резкого перехода окраски раствора из синей в бесцветную.

1) 5NaNO₂ + 2KMnO₄ + 3H₂SO₄→ 5NaNO₃ + 2 MnSO₄ + K₂SO₄ + 3H₂O

NO₂^- + H₂O - 2e→ NO₃^- + 2H⁺ 5

MnO₄^- + 8H⁺ + 5e→ 2Mn²⁺ +4H₂O 2

5NO₂^- + 2MnO₄^- + 6H⁺→5NO₃^- + 2Mn²⁺ + 3H₂O

2) 2KMnO₄ + 10KI + 8H₂SO₄ → 2 MnSO₄ + 6 K₂SO₄ + 5I₂ + 8H₂O

MnO₄^- + 8H⁺ + 5e→ 2Mn²⁺ + 4H₂O 2

2 I^- -2e → I₂ 5

2MnO₄^- + 10 I^- + 16 H⁺→ 2Mn²⁺ + 5 I₂ + 8H₂O

3) I₂ + 2 Na₂S₂O₃→ 2NaI + Na₂S₄O₆

I₂ + 2e → 2 I^- 1

2 S₂O₃^2- -2e → S₄O₆^2- 1

I₂ +2 S₂O₃^2-→ 2 I^- + S₄O₆^2-

n (¹/₅ KMnO₄) = n (¹/₂ NaNO₂) + n (¹/₂ I₂)

n (I₂) = n (Na₂S₂O₃)

n (¹/₂ NaNO₂) = n (¹/₅ KMnO₄) - n (Na₂S₂O₃)

C (¹/₂ NaNO₂) = C (¹/₅ KMnO₄)∙ V (KMnO₄) - C (Na₂S₂O₃)∙ V (Na₂S₂O₃)

V (NaNO₂)

C (¹/₂ NaNO₂) = 0,1 моль/л ∙ 10мл – 0,05 моль/л ∙3 мл = 0,085 моль/л

10 мл

m (NaNO₂)= C (¹/₂ NaNO₂) ∙M(¹/₂ NaNO₂)∙ V

m (NaNO₂) = 0,085 моль/л∙ 34,5г/моль ·10мл = 29,325г

Т (NaNO₂) = C (¹/₂ NaNO₂) ∙M(¹/₂ NaNO₂)

Т (NaNO₂) = 0,085 моль/л∙ 34,5г/моль = 0,002935 г/мл

Сравнение двух методов анализа по правильности и воспроизводимости

	Стандартизация по сульфаниловой кислоте C(1/2 NaNO2), моль/л	Стандартизация по перманганату калия C(1/2 NaNO2), моль/л
	0,084	0,083
	0,085	0,084
	0,086	0,084
	0,087	0,084
	0,087	0,0845
	0,087	0,085
	0,087	0,085
	0,087	0,085
	0,088	0,085
	0,089	0,085
	0,090	0,09

Охарактеризуем стандартизацию раствора NaNO₂ по сульфаниловой кислоте по воспроизводимости и правильности.

1) Определяем наличие грубых промахов

Q₁= 0,085- 0,084 = 0,16

0,09 – 0,084

Q₂ = 0,090- 0,089 = 0,16

0,09 – 0,084

Q_таб = 0,64 ; Q_расч = 0,16 < Q_таб = 0,64

Грубые промахи отсутствуют. Выборка однородна.

C (ср) = ( 0,084 +0,085 +0,086 +0,084 +0,087 + 0,087 +0,087 + 0,087 +0,087 + 0,088 +0,089 +0,09) моль/л / 11 = 0,087 моль/л

2) Таблица отклонений

	C	∆C	∆C2
	0,084	-0,003	0,000009
	0,085	-0,002	0,000004
	0,086	-0,001	0,000001
	0,087
	0,087
	0,087
	0,087
	0,087
	0,088	0,001	0,000001
	0,089	0,002	0,000004
	0,09	0,003	0,000009

∑∆C² = 0,0000028

3) Рассчитываем стандартное отклонение и дисперсию.

S= 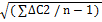= = 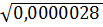0,00167

V= S² = 0,0000028

4) Рассчитываем полуширину доверительного интервала.

∆C(ср) = S∙t _0,95∙11 = 0,00167∙2,23 = 0,011

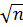
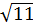
Доверительный интервал:

C(ср) ±∆C(ср) = 0,087 + 0,011

5) Рассчитываем относительную ошибку среднего

ὲ=0,011 ∙ 100% = 12,64

0,087

Охарактеризуем стандартизацию раствора NaNO₂ по перманганату калия по воспроизводимости и правильности.

1) Определяем наличие грубых промахов

Q₁= 0,084- 0,083 = 0,14

0,09 – 0,083

Q₂ = 0,090- 0,085 = 0,71

0,09 – 0,083

Q_таб = 0,64 ; Q_расч = 0,14 < Q_таб = 0,64

Q_расч = 0,71 > Q_табл= 0,64

С(NaNO₂)=0,09 – грубый промах

Q₃ = 0,085- 0,0845 = 0,071

0,09 – 0,083

Q_расч = 0,071 < Q_таб = 0,64

Грубые промахи отсутствуют. Выборка однородна.

C (ср) = ( 0,083 +0,084 +0,084 +0,084 +0,0845 + 0,085 +0,085 + 0,085 +0,085 + 0,085) моль/л / 10 = 0,0844 моль/л

2) Таблица отклонений

	C	∆C	∆C2
	0,083	-0,0014	0,00000196
	0,084	-0,0004	0,00000016
	0,084	-0,0004	0,00000016
	0,084	-0,0004	0,00000016
	0,0845	0,0001	0,00000001
	0,085	0,0006	0,00000036
	0,085	0,0006	0,00000036
	0,085	0,0006	0,00000036
	0,085	0,0006	0,00000036
	0,085	0,0006	0,00000036

∑∆C² = 0,00000249

3) Рассчитываем стандартное отклонение и дисперсию.

S= 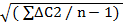=0,000525

V= S² = 0,000000276

4) Рассчитываем полуширину доверительного интервала.

∆C(ср) = S∙t _0,95∙10 = 0,000000276 ∙2,26 = 0,0000002

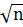
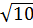
Доверительный интервал:

C(ср) ±∆C(ср) = 0,0844 + 0,0000002

5) Рассчитываем относительную ошибку среднего

ὲ=0,0000002 100% = 0,000234

0,0844

Сравним дисперсии обоих методов, рассчитав критерий Фишера.

F_расч= V₁/V₂ = 0,000000280 / 0,000000276 = 1,01

F_таб = 5,26 ; F_расч< F_таб

Различие дисперсий статистически не значимо. Дисперсии однородны.

Методы сравнимы по воспроизводимости.

Сравним средние результаты, полученные двумя методами анализа.

Выше было показано, что оба метода дают правильные результаты и следовательно результаты полученные обоими методами можно рассматривать как единую выборку, т.к. дисперсии V₁ и V₂ однородны, то рассчитаем средневзвешенную дисперсию:

V_(ср)= S_(ср)²= (n₁-1)∙V₁+(n₂-1)∙V₂ = 0,00000028∙10+0,000000276∙9 = 0,000000278

n₁ + n₂ -2 19

Вычисляем критерий Стьюдента:

t_расч= C_1(ср)- C_2(ср) ∙ 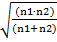= 0,087-0,0844 ∙ 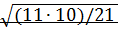= 1,12

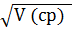0,00527

t_табл=2,85 ; t_расч< t_табл

Различие между средними C_1(ср) и C_2(ср), т.е. между результатами, полученными двумя разными методами анализа, статистически незначимо. Данные, найденные обоими методами, можно объединить в единую выборку объёмом n₁+n₂ и обрабатывать как единую выборочную совокупность вариант.